
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Функції
|
|
|
|
11.1. Зростання і спадання функції.
 |
В означенні 1.17 введено поняття зростаючої і спадної функції. В цьому параграфі покажемо, як за допомогою першої похідної досліджувати функцію на монотонність.
Теорема 11.1. Необхідною і достатньою умовою зростання неперервної на 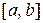 і диференційованою на
і диференційованою на 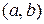 функції є невід’ємність її похідної на
функції є невід’ємність її похідної на 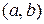 тобто:
тобто:
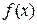 зростає на
зростає на 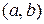
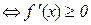 на
на 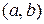 .
.
Доведення. Необхідність. Надамо аргументу х приріст 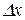 і розглянемо відношення
і розглянемо відношення
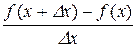 .
.
Оскільки за умовою теореми 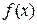 – зростаюча функція, то
– зростаюча функція, то
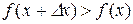 при
при 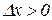 ,
,
і
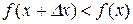 при
при  .
.
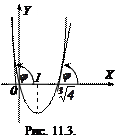 В обох випадках
В обох випадках
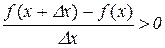 . (11.1)
. (11.1)
За умовою нашої теореми
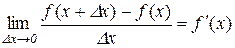 ,
,
тому з (11.1) за теоремою 3.10 маємо 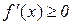 . Що й треба було довести.
. Що й треба було довести.
Достатність. Розглянемо два довільні значення аргументу х1 і х2 (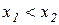 ) з відрізка
) з відрізка 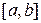 . За умовою нашої теореми на відрізку
. За умовою нашої теореми на відрізку 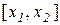 для функції
для функції 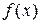 виконуються умови теореми Лагранжа, тому маємо
виконуються умови теореми Лагранжа, тому маємо
 , (11.2)
, (11.2)
де 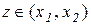 . За умовою теореми
. За умовою теореми 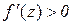 , тому з (11.2) слідує, що
, тому з (11.2) слідує, що 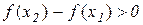 , тобто
, тобто 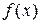 – зростаюча функція
– зростаюча функція 
Аналогічна теорема має місце і для спадної функції.
Теорема 11.2. Необхідною і достатньою умовою спадання неперервної на 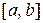 і диференційованою на
і диференційованою на 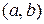 функції є недодатність її похідної на
функції є недодатність її похідної на 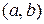 тобто:
тобто:
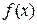 спадна на
спадна на 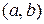
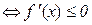 на
на 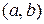
Теореми 11.1 і 11.2 мають наступний геометричний зміст:
якщо на відрізку 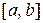 функція
функція 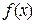 зростає, то дотична до кривої
зростає, то дотична до кривої 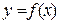 в кожній точці цього відрізку утворює з віссю ОХ гострий кут
в кожній точці цього відрізку утворює з віссю ОХ гострий кут 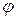 або (в деяких точках) – горизонтальна, тобто тангенс цього кута не невід’ємний
або (в деяких точках) – горизонтальна, тобто тангенс цього кута не невід’ємний 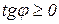 (рис. 11.1);
(рис. 11.1);
якщо функція спадна на відрізку 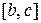 , то кут нахилу дотичної
, то кут нахилу дотичної 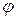 тупий або (в деяких точках) дотична горизонтальна, тобто тангенс цього кута не додатний
тупий або (в деяких точках) дотична горизонтальна, тобто тангенс цього кута не додатний 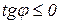 (рис. 11.2).
(рис. 11.2).
Таким чином, доведена теорема дає змогу говорити про спадання або зростання функції в залежності від знаку її похідної.
Приклад 11.1. Знайти інтервали монотонності функції
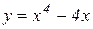 .
.
Розв’язування. Похідна функції рівна
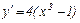 .
.
Тому при 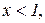 функція спадає, так як тут
функція спадає, так як тут 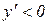 ,, а при
,, а при 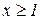 функція зростає, так як –
функція зростає, так як – 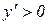 (рис. 11.3).
(рис. 11.3).
11.2. Максимум і мінімум функції.
Означення 11.1. Функція 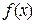 має максимум в точці х1 , якщо можна знайти окіл
має максимум в точці х1 , якщо можна знайти окіл 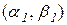 точки х1 такий, що для всіх точок
точки х1 такий, що для всіх точок 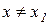 цього околу виконуватиметься нерівність
цього околу виконуватиметься нерівність 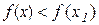 .
.
Так функція 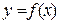 (рис. 11.4) має максимум в точках х1 і х2.
(рис. 11.4) має максимум в точках х1 і х2.
Означення 11.2. Функція 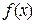 має мінімум в точці х2 , якщо можна знайти окіл
має мінімум в точці х2 , якщо можна знайти окіл 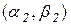 точки х2 такий, що для всіх точок цього околу виконуватиметься нерівність
точки х2 такий, що для всіх точок цього околу виконуватиметься нерівність 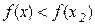 .
.
Отже, функція 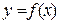 (рис. 11.4) має мінімум в точках х2 і х4.
(рис. 11.4) має мінімум в точках х2 і х4.
Зауваження 11.1. Функція, яка визначена на відрізку, може досягати максимальних і мінімальних значень тільки в точках, розташованих в середині цього відрізка.
Зауваження 11.2. Максимум і мінімум функції не завжди є відповідно найбільшим і найменшим значенням функції на розглядуваному відрізку.
 Наприклад, функція, яка зображена на рис. 11.4, найменше значення на відрізку
Наприклад, функція, яка зображена на рис. 11.4, найменше значення на відрізку  набуває в точці х2 , тобто в точці мінімуму, а найбільше – в точці b, а не х1 або х3 .
набуває в точці х2 , тобто в точці мінімуму, а найбільше – в точці b, а не х1 або х3 .
11.3. Необхідна умова існування екстремуму.
Означення 11.3. Максимуми і мінімуми функції називають екстремумами або екстремальними значеннями функції.
Сформулюємо необхідну умову існування екстремуму функції.
Теорема 11.3. Якщо диференційована функція 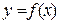 має в точці
має в точці 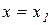 екстремум, то
екстремум, то 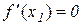 .
.
Доведення. Нехай в точці 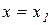 функція має максимум. Тоді з означення максимуму випливає, що при малих за абсолютним значенням приростах
функція має максимум. Тоді з означення максимуму випливає, що при малих за абсолютним значенням приростах 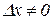 справедлива нерівність
справедлива нерівність
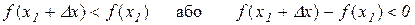 .
.
Тому знак відношення
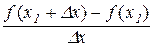
визначається знаком  , тобто
, тобто
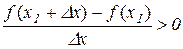 при
при  (11.3)
(11.3)

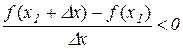 при
при 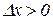 . (11.4)
. (11.4)
За означенням похідної
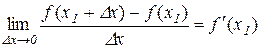 ,
,
причому значення границі не залежить від того, як 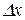 прямує до нуля (залишаючись від’ємним чи додатним). А з нерівностей (11.3) і (11.4) виходить, що
прямує до нуля (залишаючись від’ємним чи додатним). А з нерівностей (11.3) і (11.4) виходить, що
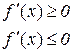
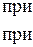
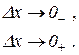 (11.5)
(11.5)
Оскільки похідна є певним значенням, то нерівності (11.5) сумісні тільки при 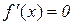 .
.
Аналогічно проводиться доведення для випадку мінімуму функції 
Геометричний зміст цієї теореми полягає в наступному (рис. 11.4): якщо в точках максимуму або мінімуму функція 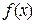 має похідну, то дотична до кривої
має похідну, то дотична до кривої 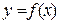 в цих точках горизонтальна. Справді, в цьому випадку
в цих точках горизонтальна. Справді, в цьому випадку 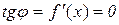 , тобто
, тобто 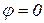 .
.
Наслідок 11.3. Диференційована на інтервалі 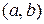 функція
функція 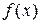 може набувати екстремуму тільки в тих точках х, де
може набувати екстремуму тільки в тих точках х, де 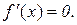 .
.
Це слідує безпосередньо з теореми 11.3 
Зворотній висновок неправильний: не при всіх значеннях аргументу, де похідна функції рівна нулю, існує максимум або мінімум функції.
Приклад 11.2. Похідна функції 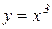 в точці
в точці 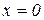 дорівнює нулю, але в цій точці функція не має ні максимуму, ні мінімуму (рис. 11.5).
дорівнює нулю, але в цій точці функція не має ні максимуму, ні мінімуму (рис. 11.5).
11.4. Достатня умова існування екстремуму.
Ми розглядали функцію, диференційовану на інтервалі. Але екстремум може досягатися і в точках, де похідна не існує.
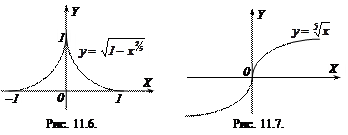
Приклад 11.3. Розглянемо функцію 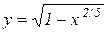 . Її областю визначення є відрізок
. Її областю визначення є відрізок 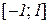 , а похідна
, а похідна

не існує в точках 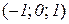 . Але в точці
. Але в точці 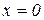 задана функція набуває максимуму:
задана функція набуває максимуму: 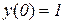 (рис. 11.6).
(рис. 11.6).
Приклад 11.4. Для функції 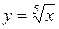 похідна
похідна

не існує при 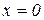 . Але в цій точці функція не має ні максимуму ні мінімуму (рис. 11.7).
. Але в цій точці функція не має ні максимуму ні мінімуму (рис. 11.7).
Таким чином, функція може набувати екстремуми тільки в точках, де похідна дорівнює нулю або не існує (зазнає розриву).
Означення 11.4. Значення аргументу, при яких похідна функції існує і дорівнює нулю або не існує (зазнає розриву), називаються критичними точками цієї функції.
Згідно з прикладами (11.2)–(11.4), не в усіх критичних точках функція набуває екстремуму.
Теорема 11.4. (достатня умова існування екстремуму). Нехай 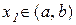 – критична точка функції
– критична точка функції 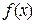 , яка є неперервною на інтервалі
, яка є неперервною на інтервалі 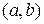 і диференційованою за всіх значень
і диференційованою за всіх значень 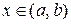 крім, можливо, точки х1 .
крім, можливо, точки х1 .
Тоді,
якщо похідна 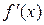 при переході аргументу через точку х1 зліва на право міняє свій знак з “ + ” на “–”, то в точці
при переході аргументу через точку х1 зліва на право міняє свій знак з “ + ” на “–”, то в точці 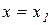 функція
функція 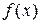 набуває максимуму;
набуває максимуму;
якщо ж знак змінюється з “–” на “ + ”, то в точці 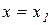 функція
функція 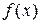 набуває мінімуму.
набуває мінімуму.
Доведення. Нехай похідна змінює знак з “ + ” на “–”, тобто для всіх значень х, досить близьких до х1 маємо:
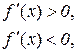
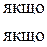
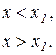
Треба показати, що 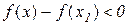 .
.
 |
З умови теореми випливає, що функція
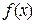 неперервна на відрізку
неперервна на відрізку 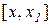 (або
(або 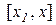 ) і диференційована на інтервалі
) і диференційована на інтервалі 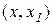 (або
(або  ), тому за теоремою Лагранжа можна записати
), тому за теоремою Лагранжа можна записати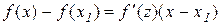 , (11.6)
, (11.6)
де z розташоване між х і х1 .
Для 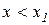 маємо:
маємо:
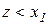 ,
, 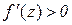 і
і 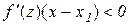 .
.
Тому з (11.6) виходить, що 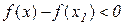 . Аналогічно для
. Аналогічно для 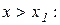 :
:
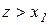 ,
, 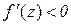 і
і 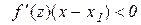 ;
;
тому – 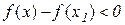 . Таким чином, для всіх значень х, досить близьких до х1 , виконується нерівність
. Таким чином, для всіх значень х, досить близьких до х1 , виконується нерівність 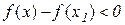 , тобто в точці х1 функція
, тобто в точці х1 функція 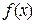 набуває максимуму.
набуває максимуму.
Аналогічно доводиться друга частина теореми – про достатню умову існування мінімуму 
11.5. Дослідження функції на екстремум за
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 518; Нарушение авторских прав?; Мы поможем в написании вашей работы!