Боковая рефракция и её влияние на результаты угловых измерений

Одним из основных источников ошибок при высокоточных угловых измерениях в триангуляции является боковая рефракция. Поднятие визирного луча над препятствиями на несколько метров уменьшает влияние боковой рефракции местного характера.

Рис.2.15. Влияние боковой рефракции

Луч света из-за различной плотности среды проходит от точки А к точке В среды не по прямой АВ, а по сложной кривой двоякой кривизны оптически кратчайшим путём АmВ (рис.2.15). Находящийся в точке А наблюдатель увидит изображение наблюдаемого предмета В не в направлении АВ, а по касательной АВ¢ к последнему элементу световой кривой АmВ в точке А. Угол В¢АВ называется углом рефракции (рефракцией) в точке А. Горизонтальная составляющая его d называется углом боковой рефракции (боковой рефракцией), а вертикальная составляющая этого угла – углом вертикальной рефракции (вертикальной рефракцией).

При больших расстояниях величина вертикальной рефракции достигает минуты и более, боковая рефракция при этом не превышает несколько секунд. Однако наличие боковой рефракции усложняет проблему точного измерения горизонтальных углов и, по существу, ограничивает дальнейшее повышение точности угловых измерений.

Различают большие (областные) и малые (местные) поля боковой рефракции. Большие поля рефракции обусловлены общим географическим распределением плотности воздуха от экватора к полюсу, в прибрежных зонах морей и океанов, вблизи горных хребтов и т.д. Такие большие поля боковой рефракции по их свойствам близки к однородным. Их влияние на направления длиной 25-30км составляет в среднем около 0,2² и носит систематический характер.

Рефракция местного происхождения обусловлена местными аномалиями плотности воздуха на пути визирного луча. При неблагоприятном стечении обстоятельств ошибки в углах и азимутах за влияние местных полей рефракции могут достигать 3-7² и более.

Средняя квадратическая величина влияния местных полей рефракции на точность угловых измерений в триангуляции высших классов составляет в среднем 0,4-0,6², а на точность определения азимутов на пунктах Лапласа – 0,6-0,8². Из-за большого разнообразия подстилающей поверхности местная рефракция в сетях триангуляции имеет случайное распределение, хотя по отдельным направлениям носит характер систематических ошибок.

Боковая рефракция d зависит от наклонов к горизонту эквипотенциальных поверхностей n=const (n – показатель преломления воздуха), а, следовательно, от метеорологических элементов и их градиентов. Эта зависимость без учёта пренебрегаемо малого влияния влажности воздуха (составляет менее 1% от d) может быть выражена формулой

d = e + s, (2.3)

где для неоднородного поля (Ñ_гn ¹ const):

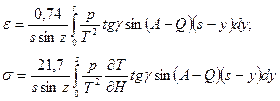(2.4)

и для однородного поля (Ñ_гn = const):

(2.5)

В формулах (2.3) - (2.5):

d - поправка в измеренное направление за влияние боковой рефракции (в секундах дуги);

s – длина визирного луча (м) по хорде, стягивающей его концы;

y – расстояние (м) по хорде от начальной точки луча до текущей;

p – давление воздуха (мм рт. ст.);

T =273, 2+ T °C – абсолютная температура Кельвина;

¶T/¶H» (T₂-T₁) / (H₂-H₁) – вертикальный градиент температуры воздуха (градус/м);

g - угол, отсчитываемый от точки зенита до вектора Ñn, направленного в сторону уменьшения n = n (X, Y, H);

A и Q – азимуты измеряемого направления и вектора Ñn соответственно, отсчитываемые по ходу часовой стрелки от оси X, направленной на север, к оси Y, направленной на восток;

z – зенитное расстояние наблюдаемой цели;

Ñ_г n – горизонтальный градиент показателя преломления воздуха.

Составляющая s отражает в первую очередь влияние местных полей боковой рефракции, а составляющая e - влияние рефракционных полей значительного протяжения. В общем случае, т. е. при e + s ¹ 0 и A ¹ Q, имеем

s = 0, если (tg γ)_s = 0.

Однако в подавляющем числе случаев наклоны tg γ на всём пути визирного луча длиной s не равны нулю. Поэтому

e ® 0, если (tg g)_s ® 0;

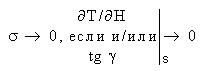
В триангуляции |s| > |e| поэтому основное внимание должно быть направлено на существенное ослабление влияний местных полей боковой рефракции (составляющей s). Заметим, что при s ® 0 и e ® 0.

Известно, что в нижнем 300-метровом слое атмосферы, в котором ведутся наблюдения на пункты триангуляции, вертикальные градиенты температуры в суточном ходе их движения в сутки (утром в момент времени t^у₀, наступающий через 1-2 часа после восхода Солнца, и вечером в момент времени t^в₀, наступающий за 1-2 часа перед заходом) переходят через нуль, изменяя в эти моменты времени всякий раз знаки на противоположные (рис.2.16).

Под воздействием суточного хода рефракции каждое измеряемое направление (касательная к последнему элементу световой кривой в точке приёма света) также испытывает суточный ход (рис.2.17). В связи с этим возникает задача учёта суточного хода измеряемых направлений при высокоточных угловых измерениях и азимутальных определениях с целью приведения (редуцирования) их результатов к определённым физическим условиям, когда влияние боковой рефракции рано или почти равно нулю.

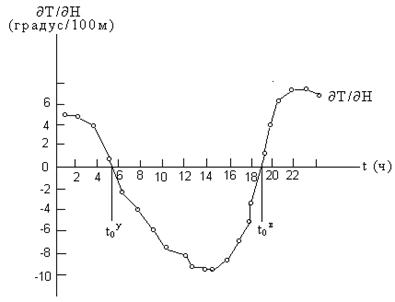
Рис.2.16. График суточного хода вертикальных градиентов температуры воздуха в открытой местности (среднее за июнь)

Так как на двух-, трёхчасовом отрезке времени в окрестности моментов t₀, когда обычно измеряют горизонтальные углы в триангуляции, температурные градиенты, а, следовательно, и функционально связанная с ними боковая рефракция изменяются во времени практически линейно и, переходя через нуль, меняют знаки на противоположные, то отсюда вытекает простой и в то же время эффективный способ почти полного исключения влияний местных полей боковой рефракции из результатов наблюдений.

Рис.2.17. График изменения во времени угла β земного предмета под воздействием суточного хода боковой рефракции

Суть этого способа сводится к тому, что в нижнем 300-метровом слое атмосферы горизонтальные направления (углы и азимуты) надо либо измерять симметрично во времени относительно среднего момента t₀ изотермии воздуха на высоте визирного луча и выводить среднее из результатов измерений, либо редуцировать результаты измерений на момент времени t₀ в случае асимметричных наблюдений.

В массовых работах по высокоточным угловым измерениям в триангуляции целесообразно распределять приёмы измерения направлений симметрично во времени относительно момента времени t₀, когда наступают наиболее спокойные и чёткие изображения визирных целей, характерные для периода изотермии воздуха на высоте визирного луча. Редуцирование асимметричных измерений используется при обработке результатов измерений повышенной точности, в первую очередь при определении азимутов на пунктах Лапласа.

Горизонтальные направления β, измеренные в течение нескольких вечеров не менее чем 15-18 круговыми приёмами на отрезке времени (t_нач < t₀ < t_кон) £ 2-3 ч, могут быть редуцированы на средний на пункте момент x₀ вечерней изотермии воздуха по формуле

β₀ = β + k (x₀ –x), (2.6)

где β₀ – исправленное за рефракцию значение угла;

β – среднее значение угла из приёмов;

k – часовое изменение этого угла;

x₀=t₀ – t _зах ; t _зах - момент захода Солнца;

x – среднее по приёмам время наблюдений на пункте;

k(x₀ – x) = δ – поправка за асимметрию времени наблюдений, или, что то же самое, поправка за влияние рефракции.

В формуле (2.6) неизвестными являются часовые изменения k и моменты времени x₀. Часовые изменения вычисляются по формуле

, (2.7)

где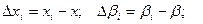

- время и результаты измерений угла в отдельных приёмах;

- средние значения времени и угла из всех приёмов.

Часовые изменения вычисляют на пункте для каждого угла, отсчитываемого от начального направления, причём отдельно для вечерних и утренних наблюдений.

Из статистических данных установлено, что в триангуляции 2 класса часовые изменения углов треугольников колеблются от 0 до ±3² в час и равны в среднем ±0,7² в час; асимметрия времени наблюдений на пунктах в разных физико-географических условиях изменяется от 0 до ±2ч, а поправки в углы треугольников за рефракцию колеблются от 0 до ±1,6². После введения поправки за рефракцию вес измеренного угла возрастает в среднем в 1,7 раза.

Выгоднейшее время наблюдений в триангуляции следует рассматривать с двух точек зрения:

• с точки зрения наилучших условий видимости, минимальных колебаний и высокого качества изображений визирных целей;
• с точки зрения наименьшего влияния местных полей рефракции на результаты измерений.

Такие благоприятные для наблюдений условия имеют место вечером и утром, особенно в периоды, когда в слое воздуха на высоте визирного луча наблюдается состояние, наиболее близкое к изотермии (рис.2.16). Продолжительность этого благоприятного для наблюдений отрезка времени зависит от многих факторов и изменяется в вечерние часы от нескольких десятков минут в полупустынных и степных районах в тихую безоблачную жаркую погоду летом до нескольких часов в холодную и ветреную погоду при наблюдениях в горных и северных районах. Заканчивать наблюдения рекомендуется примерно за полчаса до захода Солнца. Наблюдения следует вести на спокойные и слегка колеблющиеся изображения визирных целей, когда случайные их колебания не превышают 2².

Дата добавления: 2014-11-18