Поверхности вращения второго порядка

При вращении кривой второго порядка вокруг её оси образуется поверхность вращения второго порядка.

Рассматриваются следующие типы поверхностей второго порядка:

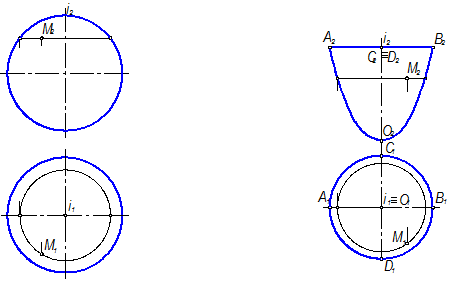
а) сфера, которая образуется вращением окружности вокруг собственной оси в соответствии с рисунком 1.3.41;

б) параболоид вращения, образуемый вращением параболы вокруг собственной оси в соответствии с рисунком 1.3.42;

в) эллипсоид вращения, который образуется вращением эллипса вокруг собственной оси. Принимая за ось вращения малую либо большую ось эллипса, получаем соответственно сжатый или вытянутый эллипсоиды вращения в соответствии с рисунком 1.3.43;

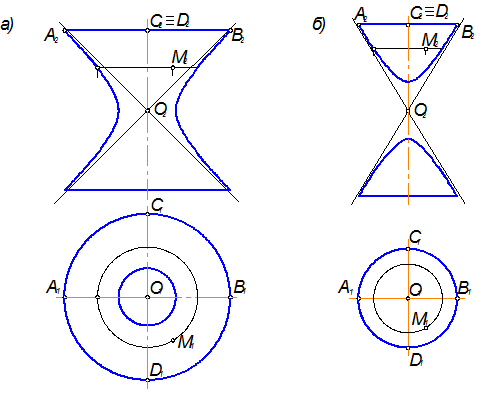
г) однополостный гиперболоид вращения, который образуется вращением гиперболы вокруг её мнимой оси в соответствии с рисунком 1.3.44, а;

д) двухполостный гиперболоид вращения, образуемый вращением гиперболы вокруг её действительной оси в соответствии с рисунком 1.3.44, б;

е) конус вращения, образуемый вращением прямой линии вокруг неподвижной оси, при этом образующая во всех своих положениях пересекает ось в некоторой точке, называемой вершиной конуса (рисунок 1.3.45);

ж) цилиндр вращения, образуемый вращением прямой линии вокруг неподвижной оси и расположенной параллельно этой оси (рисунок 1.3.45).

Положение точки на поверхности вращения второго порядка определяют при помощи параллели или (в случае конуса и цилиндра) прямолинейной образующей, проходящих через эту точку, в соответствии с рисунками 1.3.41, 1.3.42, 1.3.43, 1.3.44, 1.3.45.

В технических деталях часто встречается поверхность вращения, называемая тором. Эта поверхность получается при вращении окружности вокруг оси, расположенной в плоскости этой окружности, но не проходящей через её центр в соответствии с рисунком 1.3.46.

Рисунок 1.3.41 – Сфера Рисунок 1.3.42 – Параболоид вращения

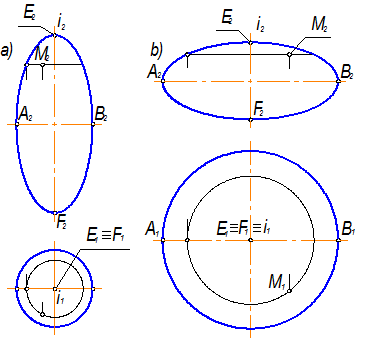
Рисунок 1.3.43 – Эллипсоид вращения

В зависимости от соотношения величин радиуса образующей окружности r и расстояния от центра окружности до оси R, возможны три разновидности поверхности:

1) r<R – окружность не пересекает ось – открытый тор (кольцо) в соответствии

с рисунком 1.3.46;

2) r=R – окружность касается оси – закрытый тор в соответствии с рисунком 1.3.47, а;

3) r>R – окружность пересекает ось – закрытый тор в соответствии с рисунком 1.3.47, б.

Произвольная прямая пересекает тор в четырёх точках и, следовательно, это поверхность четвёртого порядка.

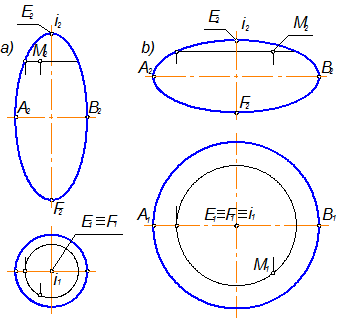Рисунок 1.3.44 – Однополостный и двуполостный гиперболоиды вращения

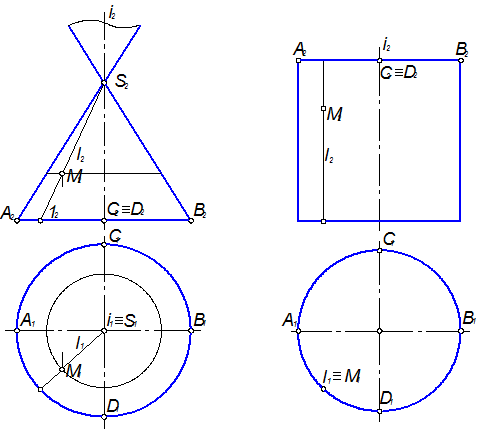Рисунок 1.3.45 – Конус вращения и цилиндр вращения

Рисунок 1.3.46 – Открытый тор

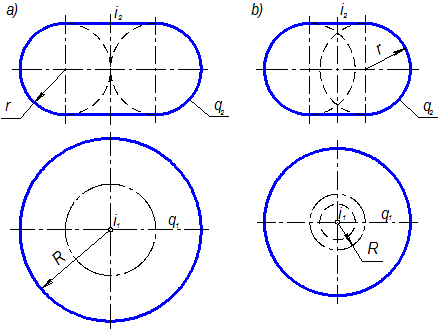Рисунок 1.3.47 – Закрытый тор

Дата добавления: 2014-11-18