Способ вращения вокруг проецирующей оси

Способ вращения

Этот способ является частным случаем способа плоскопараллельного перемещения.

Действительно, если в способе плоско-параллельного перемещения точка фигуры описывала некоторую плоскую кривую, параллельную плоскости проекции, то в этом способе точка описывает дугу окружности, плоскость которой также параллельна плоскости проекции. Поэтому графические и аналитические алгоритмы построения соответственных точек в этих способах не отличаются в целом. Способ вращения является, в ряде случаев, более удобным для решения задач.

При решении задач способом вращения положение заданных геометрических элементов изменяют путем вращения их вокруг некоторой оси.

Если ось вращения расположить перпендикулярно к плоскости проекций, то траектория вращения точки на эту плоскость проецируется окружностью, а угол поворота точки будет проецироваться в натуральную величину.

На рисунке 1.4.13 данная точка А повернута вокруг горизонтально проецирующей оси i на угол φ. Для этого:

1) Через точку А проведена плоскость вращения Ρ _┴ i;

2) Центром вращения будет являться точка пересечения плоскости Ρ с осью i (Ρ ∩ i=C);

3) Окружность, описываемая точкой А и имеющая радиус R=AC, проецируется на горизонтальную плоскость проекций в натуральную величину, а на плоскость П₂ в виде отрезка прямой, перпендикулярной к соответствующей проекции оси вращения – i₂.

4) При повороте точки А на угол φ до положения А¹, горизонтальная проекция точки А₁ будет перемещаться по окружности, а фронтальная А₂ – по прямой, параллельной оси х.

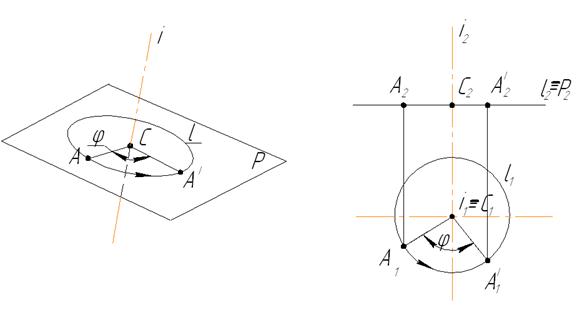
Рисунок 1.4.13 – Вращение точки вокруг проецирующей оси

Дата добавления: 2014-11-18