Моделювання процесу в шару каталiзатора. 2 страница

Звичайно для нормалізації застосовується можливий діапазон зміни значень незалежних перемінних, котрий завжди може бути установлений виходячи з фізичної сутності розв'язуваної задачі.

Наприклад, нехай деякий фізичний параметр вихідної задачі може змінювати своє значення а в межах:

a_Jmin< a_J < a_Jmax (5.8)

Тоді, позначаючи величину діапазону зміна значення а_J через

d_J=a_{J min}- a_{J min},

можна ввести безрозмірну перемінну U_J:

U_J = (a_J - a_Jmin)/d_J (5.9)

Перемінна U_J при такому способі визначення буде змінюватися в межах:

0<U_J<1 (5.10)

Нормалізація значно спрощує організацію алгоритмів оптимізації і дозволяє будувати уніфіковані алгоритми пошуку. Необхідно тільки передбачати

прямє і зворотне перерахування фізичних параметрів

Рис. 5.2

5.2.2. Геометрична інтерпретація цільової функції

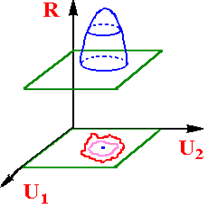Відповідно до співвідношення (5.6) значення критерію оптимальності R може розглядатися як функція, обумовлена в n-мірному просторі перемінних U_J (j=1,2,...n). Оскільки наочне графічне зображення n-мірного простору відсутнє, використається наступний метод представлення функції R(U) на плоскому кресленні (рис.5.3).

Використовуємо наступний підхід. Допустимо, що задача оптимізації виречена і екстремум знайдений. Проведемо через крапку U_опт у n-мірному просторі двовимірну площину Р. Тоді при видаленні від крапки U_опт у будь-якому напрямку R(U) буде змінюватися.

Якщо R(U) є безупинної функцією від U, те навколо крапки U_опт завжди можна провести в даної площини замкнуту лінію, на якій значення R(U) буде постійним. Таких замкнутих ліній, називаних

Рис. 5.3 лініями постійного рівня, що відповідають різних значень R(U)=С_k, можна провести площини Р навколо крапки U_опт скільки завгодно, причим кожна з цих ліній (наприклад, для випадку пошуку мінімуму) буде цілком охоплювати будь-яку лінію постійного рівня, для якої значення R(U) менше. Форма ліній постійного рівня, відповідаючим різним значенням С_k може при цьому бути дуже різної.

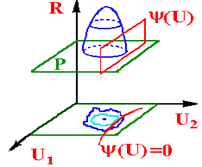
При наявності обмежень типу (5.7а), розглянутий прийом зображення цільової функції також можна використовувати, якщо прийняти до уваги, що кожне з рівнянь (5.7а) визначає в n-мірному просторі (n-1)-мірну поверхню, перетинання якої з двовимірної площиною Р має вид деякої лінії L (рис.5.4).

Рис.5.5

Рис.5.4

Обмеження типу нерівностей (5.7б) незалежно від їхнього числа також представляються описаним способом (рис.5.5).

Розглянутий спосіб не є єдиним і однозначної, так як. форма ліній постійного рівня функції R(U) і обмежень може істотно змінюватися в залежності від орієнтації двовимірної площини Р в n-мірному просторі. Однак цей спосіб найбільше простий і дозволяє наочно представити різні алгоритми рішення

задач нелінійного програмування.

5.2.3. Особливі крапки і лінії цільової функції

Нагадаємо, що необхідною умовою існування екстремуму функції багатьох перемінних є виконання системи рівнянь

dR/dU_j=0, j=1,2,...,n (5.11)

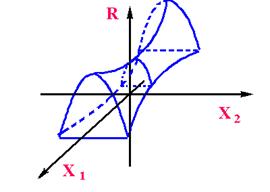Оскільки умова (5.11) необхідне, але ще недостатнє, можуть представитися випадки, коли при його виконанні в деякій крапці U_s екстремуму функції R(U) у ній не буде – так звані "сідлови" крапки (рис.5.6).

Іншим типом особливостей цільової функції є так називані "яри", при наявності яких уздовж визначених напрямків величина цільової функції змінюється дуже слабко. Як приклад можна привести рівняння еліпса, 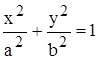, коли а > в (рис.5.7):

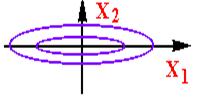
Рис.5.6

У загальному випадку лінія "дна яру" може не збігатися по напряму Рис.5.7

з осями координат і, крім того, істотно

відрізняється від прямої, тобто можливі також "криволінійні яри"

(рис.5.8).

Рис.5.8

5.2.4. Глобальний і локальний оптимуми

При відшуканні оптимуму цільової функції R(U) задачею, як правило, є визначення сукупності значень незалежних змінних U_j, що відповідає не якому-небудь екстремуму функції R(U), а найбільшому чи найменшому значенню R(U_j) у припустимої області Vдоп. Якщо шукається, наприклад, мінімум, то рішення задачі оптимізації повинне задовольняти умові:

R(U_опт) < R(U) (5.12)

причому U Î V.

Умова (5.12) повинна виконуватися для будь-яких припустимих значень U.

Оптимум, для якого справедливо умова (5.12), звичайно називається гло-

бальним. Крім нього функція R(U) може

мати один чи трохи локальних

екстремумов (рис.5.9). У цьому випадку

складність задачі пошуку екстремума

для функції багатьох перемінних значно

збільшується.

Рис.5.9

5.3. Методи рішення задач оптимізації

Вибір методу рішення - один з найважливіших етапів оптимізації.

Можна виділити наступні групи методів:

- аналітичні методи;

- методи математичного програмування.

Розглянемо більш докладно групи цих методів і деякі з них.

Група аналітичних методів оптимізації поєднує аналітичний пошук екстремуму функції, метод множників Лагранжа, вариаційні методи і принцип максимуму.

Аналітичний пошук екстремуму функції, заданих без обмежень на незалежні перемінні, застосовується до задач, у яких оптимізуєма функція має аналітичне вираження, що диференцується у всьому діапазоні дослідження, а число перемінних невелике. Це один з найбільш простих методів.

Група методів математичного програмування включає динамичнє програмування, лінійне програмування і нелінійне програмування.

Динамічне програмування - ефективний метод рішення задач оптимізації багатостадійних процесів. Метод припускає розбивку аналізованого процесу на стадії (в часі чи в просторі)- наприклад, реактор у каскаді чи тарілка в колоні. Розгляд задачі починається з останньої стадії процесу й оптимальний режим

визначається постадійно.

Лінійне програмування - метод для рішення задач оптимізації з лінійними вираженнями для критерію оптимальності і лінійними обмеженнями на область зміни перемінних. Подібні задачі зважуються ітераційними способами. Ці методи використовуються при оптимальному плануванні виробництва при обмеженій кількості ресурсів, для транспортних задач і ін.

Методи нелінійного програмування- поєднують різні способи рішення оптимальних задач: градієнтні, безградієнтні і випадкового пошуку. Загальним для методів нелінійного програмування є те, що їх використовують при рішенні задач з нелінійними критеріями оптимальності. Усі методи нелінійного програмування - це чисельні методи пошукового типу. Суть їх - у визначенні набору незалежних перемінних, що дають найбільше збільшення оптимізуємої

функції. Дана група методів застосовується як для детерминованіх, так і стохастичних процесів.

5.4.Аналітичні засоби

Аналітичні засоби засновані на класичних засобах математичного аналізу.

Задача оптимізації формулюється наступним чином. Існує процес, відома його математична модель та встановлений критерій оптимізації R у вигляді функції:

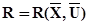(5.13)

або функціонала:

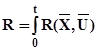, (5.14)

де .

Задані обмеження:

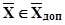та 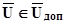. (5.15)

Необхідно при заданих обмеженнях знайти такі значення , при яких R досягає екстремуму. У випадку функціонала R необхідно знайти вид функції ,при якої R досягає екстремуму.

Аналітичні засоби пошуку екстремуму критерію оптимальності застосовуються до задач, у яких оптимiзуєма функція має аналітичний вираз, а число перемінних невелике.

У вигляді прикладу розглянемо визначення оптимального часу перебування суміші у РІВ.

Для двох послідовних реакцій 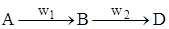необхідно визначити оптимальний час перебування t, при якому вихід целевого продукту В буде досягати максимуму.

Нехай а - початкова концентрація компоненту А. В початковий момент часу концентрації компонентів В та D дорівнюють нулю: при t = 0: C_B = С_D = 0. Критерій оптимізації: вихід цільового продукту 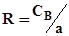. Керуючий вплив - час перебування t. Характер зміни концентрацій компонентів в часу приведений на рис 5. 10.

Нехай реакції протікають по першому порядку.

Швидкість реакцій

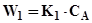(5.16)

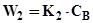(5.17)

(5.18)

Із (5.16) знайдемо вираз для поточної концентрації С_А.

;

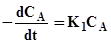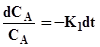
Проiнтегрiровав, одержимо:

(5.19).

Рис. 5. 10 Підставимо (5.19) та (5.17) в (5.18):

,

або

. (5.20)

Розв'язав одержане рівняння, знайдемо вираз для визначення поточної концентрації компонента В:

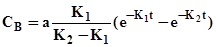. (5.21)

Вихід цільового продукту R=C_B/a = 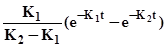. (5. 22)

Дослідимо екстремум одержаної цільової функції (5.22). Умови існування максимуму: 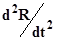<0.

Знайдемо першу похідну і прирівняємо її нулю:

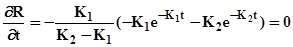. (5.23)

Вирішив одержане рівняння, визначимо оптимальний час перебування:

. (5.24)

Для перевірки виконання достатньої умови існування максимуму обчислюємо другу похідну:

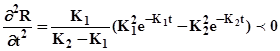
Так як друга похідна менш 0, отже у наданій точці існує максимум цільової функції R.

Підставив (5.24) у (5.21), одержимо вираз для визначення максимальної концентрації компонента В:

. (5.25)

5.5. Загальна характеристика засобів рішення задач

нелiнійного програмування

Коли цільова функція (5.6) і обмеження (5.7) нелінійні та для пошуку точки екстремуму не можна або дуже складно використовувати аналітичні засоби рішення, тоді для рішення задач оптимізації застосовуються засоби нелiнійного програмування. Як правило, при рішенні задач засобами нелінійного програмування використовуються численні засоби з застосуванням ЕОМ.

В основному засоби нелiнійного програмування можуть бути охарактеризовані як багатокрокові засоби чи засоби наступного поліпшення вихідного рішення. У цих задачах звичайно заздалегідь не можна сказати, яке число кроків гарантує знаходження оптимального значення з заданою мірою точності. Крім того, у задачах нелiнійного програмування вибір величини кроку представляє серйозну проблему, від успішного рішення якої залежить ефективність застосування того чи іншого засобу. Розмаїтість засобів рішення задач нелiнійного програмування якраз і пояснює прагнення знайти оптимальне рішення за найменше число кроків.

Більшість засобів нелiнійного програмування використовують ідею руху у n-мірному просторі в напрямку оптимуму. При цьому із деякого вихідного чи проміжного стану U^k здійснюється перехід в наступний стан U^k+1 зміною вектору U^k на величину ΔU^k, що називається кроком, тобто:

U^k+1=U^k+ΔU^k (5.26).

В ряді засобів крок, тобто його величина і напрямок визначається як деяка функція стану U^k:

ΔU^k=f(U^k) (5.27)

Отже, згідно з (5.26) новий стан U^k, що одержується внаслідок виконання кроку (5.27) може розглядатися як функція вихідного стану

U^k+1=U^k+f(U^k). (5.28)

У деяких засобах ΔU^k зумовлено не тільки станом U^k, але і рядом попередніх станів:

ΔU^k=f(U^k),U^k-1…,U^k-2 (5.29)

U^k+1=U^k+f(U^k),U^k-1…,U^k-2. (5.30)

Природно, що алгоритми пошуку типу (5.30) є більш загальними і принципово спромагаються забезпечити більш високу сходимість до оптимуму, тому що використовують більший обсяг інформації про характер поводження оптимальної функції.

У теперішній час для рішення подібних задач розроблено значне число засобів, проте не можна віддати перевагу якому-небудь одному. Вибір засобу визначається складністю об'єкту і задачею оптимізації, що вирішується. Засоби нелiнійного програмування відповідно до засобу визначення кроку пошуку 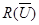можна віднести до одного із 3-х типів: безградієнтні засоби; градiєнтні засоби; засоби випадкового пошуку.

Всі ці засоби можна назвати прямими ітеративними засобами.

5.6. Градiєнтні методи рішення задач оптимiзації

5.6.1. Градієнт цільової функції

Серед засобів, що застосовуються для рішення задач нелінійного програмування, чимале місце займають засоби пошуку рішення, засновані на аналізі похідної оптимiзуємої функції. Припускаємо надалі, що аналізується тільки диференційовані функції R(U). Розглянемо властивості цих функцій, які можна використовувати для аналізу їх поведінки.

В просторі n перемінних U_j, де визначена функція R(U) проводимо лінію у довільному напрямі L

Розглянемо значення функції R(U) у 2-х крапках U та U^*, розміщених на ції прямій. Якщо скласти відношення

Рис. 5. 11

та направити довжину відтинку U^* - U до нуля, то у межі одержимо величину, становлячи похідною від функції R(U) по напрямку L, тобто

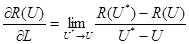(5.31)

Знайдена похідна характеризує швидкість зміни функції R(U) у точці U за напрямком L. Оскільки через точку U можна провести нескінченну множину прямих по різноманітним напрямкам, отже, у кожній точці для функції R(U) можна визначити незчисленну множину похідних за різними напрямками.

Неважко показати, що всі ці похідні можуть бути виражені через похідні за координатами, число яких вже буде кінцевим і рівним розмірності n. За правилом диференціювання складних функцій:

(5.32)

Розрахунок величин dU_j/dL розглянемо на слідуючому прикладі. В просторі 2-х перемінних U₁ та U₂ проведена пряма L (рис. 5.12).

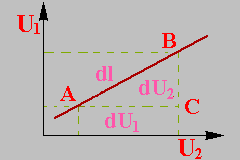Елемент довжини 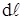в даному випадку можна виразити через диференціали перемінних

(5.33)

При цьому, з прямокутного трикутника АВС можна записати

Рис.5.12 (5.34)

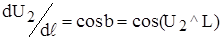
Аналогічно, для многомірного випадку є ані що інше, як направляючі косинуси обраного напрямку L по відношенню до осей координат

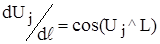(5.35)

Тоді, рівняння (5.32) можна записати

(5.36)

Розглянемо одну з поверхней постійного рівня функції R(). Ця поверхня характеризується тим, що у будь-якій її точці цільова функція R() має одне й теж саме постійне значення С. Рівняння наданої поверхні може бути одержано з виразу для цільової функції (5.6) порівнюванням його до постійної величині C:

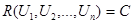(5.37)

Вирішуючи рівняння (5.37) щодо будь-якої з перемінних, можна збудувати зазначену поверхню, задаючись різноманітними значеннями інших перемінних.

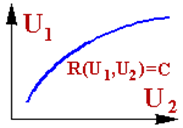Оскільки поверхня постійного рівня (5.37) має n-1 незалежних параметрів, очевидно, її можна представити як поверхня з n-1 вимірами. Так, наприклад, у просторі 2-х перемінних, тобто на площині, ця поверхня вироджується у деяку лінiю, що має тільки один вимір - довжину (рис. 5.13).

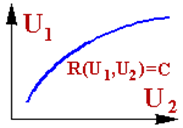
Рис.5.13

Рис.5.14

В просторі трьох перемінних поверхня постійного рівня, визначена для функції R(U₁, U₂, U₃), має вже два виміру - довжину та ширину (рис. 5.14). Аналогічно у n-мірному просторі поверхня постійного рівня функції R(), що описується рівнянням (5.37), має n-1 вимір. Таким чином, у кожній точці поверхні у n-мірному просторі можна провести n-1 взаємоперпендикулярних дотичних у відповідності з числом вимірів цієї поверхні. Крім отого, в цій точці можна провести вісь, перпендикулярну всім дотичним та, отже, спрямовану по нормалi до поверхні. У вигляді зразку розглянемо випадок, коли число керуючих впливів n=3 (рис. 5.15).

Дотичні та нормаль можуть розглядатися як система координат з початком у обраній точці поверхні.

Рис. 5.15

Надана система координат володіє однією важливою властивістю.

Часткові похідні від функції R(U) за напрямками осей, що є дотичними до поверхні, дорівнюють нулю, тому що вдовж цих напрямків функція R(U) зберігає постійне значення, оскільки розглядається поверхня постійного рівня функції R(U).

Якщо взяти довільний напрямок L, то похідна по ньому, на підставі сказаного, буде мати вигляд:

(5.38)

Це слідує з рівняння (5.36), де похідні по всім осям, за винятком нормалi N, дорівнюють 0. Оскільки cos(α) є функція, що не перевищує по абсолютній величині 1 та приймає максимальне значення при α =0, отже очевидно, що напрямок, за яким похідна dR/dL має максимальне значення, співпадає з напрямком нормалi до поверхні постійного рівня функції R(U).

Якщо відкласти на напрямку нормалi вектор з алгебраїчною величиною, рівною похідної dR(U)/dL, то отримаємо вектор, що називається градієнтом скалярної функції R(U) в точці U.

Основною властивістю градієнту функції R(U), що позначається як grad R(U) або DR(U), є те, що вектор DR(U) в кожній точці області визначення функції R(U) спрямований за напрямком нормалi до поверхні рівня, проведеної крізь цю точку, та за алгебраїчною величиною дорівнює похідній від зазначеної функції за напрямком нормалi.

5.6.2. Обчислення похідних цільової функції

В основу градiєнтних засобів пошуку оптимуму покладені обчислення та аналіз похідних цільової функції R(U). Якщо аналітичний вигляд R(U) відомий, то обчислення похідних dR/dU_j частіше всього не складає особливих труднощів. Інакше єдиним засобом визначення похідних є чисельні засоби.

Значення похідної може бути обчислено за формулою:

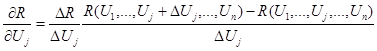(5.39)

де ΔU_j – величина приросту незалежної перемінної U_j.

Формула (5.39) дає лише наближене значення похідної. Точність наближення залежить від величини припущення ΔU_j.

Методів провіщання найкращого значення ΔU_j не існує. Практично для визначення прийнятної величини припущення(особливо на початку пошуку, коли похідні ще не знаходились) використовується метод дробіння ΔU_j. Наприклад, розраховується значення похідної з припущенням, рівним ΔU_j. Після цього розрахунок повторюється з ΔU_j/2. Якщо отримані значення похідних розрізняються істотно, то розрахунок повторюється з ΔU_j/4 і т.д., поки не буде знайдено прийнятне значення припущення. На наступних кроках пошуку це значення припущення може уточнюватися.

5.6.3. Засіб релаксації.

Алгоритм засобу являє собою пошук осьового напрямку, вдовж якого цільова функція зменшується найбільш сильно. Для цього в початковій точці пошуку визначають похідні оптимiзуємої функції по всім незалежним перемінним. Осьовому напрямку з найскорішим спаданням цільової функції, очевидно, відповідає найвелика за модулем похідна. Якщо знак похідної від'ємний, то цільова функція зменшується у напрямку осі, якщо позитивний - то у протилежному напрямку.

За напрямком спадання цільової функції виконуються кроки до тих пір, поки не буде отримане мінімальне значення за обраним осьовим напрямком. Тоді знов визначають похідні по всім напрямкам, за винятком того, по якому здійснюється спуск. Знову знаходять осьовий напрямок найскорішого спадання цільової функції, по якому виконуються подальші кроки і т.д.

Критерієм закінчення пошуку оптимуму є досягнення такої точки, при руху з якої по будь-якому осьовому напрямку подальшого спадання функції не походить.

На практиці, для признаку оптимуму часто застосовують умову:

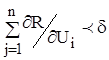(5.40)

Умова (5.40) може бути використана у отому випадку, коли оптимум лежить всередині допустимої області зміни незалежних перемінних. Якщо ж оптимум припадає на межу області допустимої зміни перемінних V, тоді критерій (5.40) не придатний та замість нього треба застосовувати умову позитивності всіх похідних за допустимими осьовими напрямками. При цьому допустимим осевим буде напрямок всередині області V.

Алгоритм спуску для обраного осьового напрямку може бути записаний у вигляді:

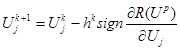(5.41)

Причому:

- значення змінюємої перемінної на к-ом кроку спуска;

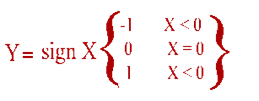
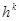- величина к-го кроку, що може змінювати своє значення залежно від номеру крока;

sign - функція знаку ("сiгнум");

U^p - вектор точки, у якій останній раз виконувалось обчислення похідних цільової функції.

Очевидно, що швидкість руху до мінімуму залежить від отого, наскільки вдало обрано крок 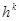зміни незалежних перемінних.

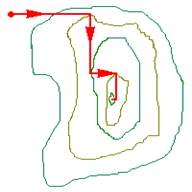Графічне зображення руху від вихідного стану до оптимального показано на рис. 5.16.

При занадто малій величині кроку число кроків, що необхідно зробити, щоб досягнути оптимума, буде великим та, отже, буде потрібний великий обсяг розрахунків. Якщо ж величина кроку обрана великою, то поблизу оптимуму може відбуватися "нишпорення", тому що при великій величині кроку мала імовірність попадання в околицю оптимуму, в якій виконується умова (5.40). Рис.5.16

Найпростіший алгоритм використання перемінного кроку пошуку складається в наступному. На початку спуска по одному з осьових напрямків задається деякий крок h. З цим кроком виконується спуск по обраному осьовому напрямку до отих пір, поки для двох наступних обчислювань значення цільової функції виконується умова (при пошуку мінімуму)

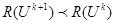
При порушенні умови на будь-якому кроці напрямок спуска по осі змінюється на протилежний, та спуск продовжується з останньої разрахованої точки зі зменшеною вдвічі величиною кроку. Цей алгоритм може бути записаний наступним чином:

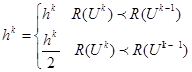(5.42)

Внаслідок використання такої стратегії крок спуска по осьовому напрямку буде зменшуватися в районі мінімуму цільової функції по цьому напрямку та пошук мінімуму можна припинити, коли величина кроку h^k стане менше заданої точності визначення мінімуму e у осьовому напрямку.

Після цього знаходиться новий осьовий напрямок, в якому функція змінюється найбільш сильно. Початковий крок по новому напрямку вже можна обрати з урахуванням величини кроку по попередньому напрямку. Це дозволяє автоматично зменшувати початковий крок по мірі наближення до оптимуму, у районі якого спуск по кожній осі проходить на невелику віддаль.

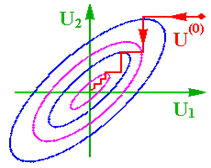Істотною особливістю метода релаксації є залежність часу пошуку від орієнтації системи координат (рис. 5.17 та 5.18).

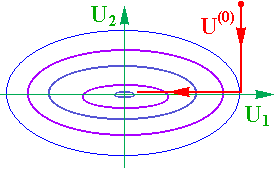
Рис.5.17 Рис.5.18

У першому випадку для досягнення мінімуму цільової функції необхідно тільки два циклу руху уздовж осьових напрямків, в другому число таких циклів зростає надто істотно. При використанні метода релаксації інколи виникають чималі труднощі:

Дата добавления: 2014-11-18