Алгебра логики

Д е л е н и е

Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.

Пример 9. Разделим число 30 на число 6.

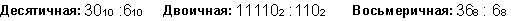
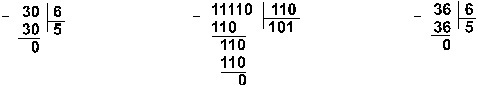
Ответ: 30: 6 = 5₁₀ = 101₂ = 5₈.

Пример 10. Разделим число 5865 на число 115.

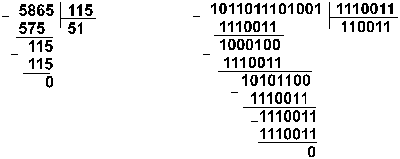
Восьмеричная: 13351₈:163₈

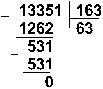
Ответ: 5865: 115 = 51₁₀ = 110011₂ = 63₈.

Проверка. Преобразуем полученные частные к десятичному виду:

110011₂ = 2⁵ + 2⁴ + 2¹ + 2⁰ = 51; 63₈ = 6^. 8¹ + 3^. 8⁰ = 51.

Пример 11. Разделим число 35 на число 14.

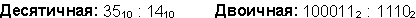
Восьмеричная: 43₈: 16₈

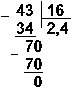
Ответ: 35: 14 = 2,5₁₀ = 10,1₂ = 2,4₈.

Проверка. Преобразуем полученные частные к десятичному виду:

10,1₂ = 2¹ + 2 ^-1 = 2,5;

2,4₈ = 2^. 8⁰ + 4^. 8^-1 = 2,5.

Логика – наука, изучающая законы и формы мышления.

Историческая справка. Этапы развития логики:

I этап – формальная логика. Основатель Аристотель (384-322 гг. до н.э.), ввел основные формы абстрактного мышления.

II. этап – математическая логика. Основатель немецкий ученый и философ Лейбниц (1642-1716), предпринял попытку логических вычислений.

III этап – математическая логика (булева алгебра). Основатель – английский математик Джордж Буль (1815-1864), ввел алфавит, орфографию и грамматику для математической логики.

Первые учения о формах и способах рассуждений возникли в странах Древнего востока (Китай, Иран), но в основе современной логики лежат учения, созданные древнегреческими мыслителями.

Свое понимание окружающего мира человек формирует в форме высказываний, утверждений.

Высказывание – повествовательное предложение, о котором можно сказать, истинно оно или нет.

Высказывание может быть выражено с помощью формальных языков.

Например:

1. Земля – планета солнечной системой. (истинное)

2. 1+6=10 (ложное)

Высказывания бывают простыми и сложными:

Простое высказывание – содержит только одну простую мысль.

Например: Ромб – квадрат.

Сложное высказывание содержит несколько простых мыслей, соединенных между собой с помощью логических операций (и, или, не).

Например: Идет дождь или Светит солнце.

Алгебра высказываний была разработана для того, чтобы можно было определить истинность или ложность составных высказываний, не вникая в их содержание.

Простым высказываниям ставятся в соответствие логические переменные, обозначаемые прописными буквами латинского алфавита.

А= «Два умножить на два равно четыре»=1

В= «4+10=20»=0

Истинному высказыванию соответствует значение логической переменной 1, а ложному – 0.

В алгебре высказываний над высказываниями можно производить определенные логические операции, в результате которых получаются новые, составные высказывания.

Составное высказывание обозначается F(A,B).

Для определения истинности или ложности составного высказывания используют таблицу истинности, в которой перечисляются всевозможные значения входящих логических переменных и соответствующие значения функций.

Количество строк q определяется по формуле q=2ⁿ, где n – количество логических переменных.

Рассмотрим логические операции:

Отрицание (Инверсия) – делает истинное высказывание ложным и, наоборот, ложное – истинным.

Обозначается: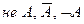

Таблица истинности:

А	не А

Например:

А = {На улице идут снег}

не А = {Неверно, что на улице идет сне}

не А = {На улице не идет снег}

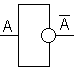– инвекртор.

Логическое умножение (конъюнкция)– истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.

Обозначается: &.

Таблица истинности:

А	В	F

Например:

А={Идет дождь}and{светит солнце}.

В={2+6=8}^{20*2=40}

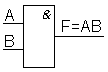– конъюнктор.

Логическое сложение (дизъюнкция) – истинно тогда, когда истинно хотя бы одно из входящих в него высказываний.

Обозначается: +, или, or, Ú.

Таблица истинности

А	В	F

Например:

А={5+9=14}или{10*3=20}

В={Олег блондин}Ú{Олег брюнет}

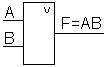– дизъюнктор.

Закрепление материала. Придумайте высказывания о себе. Пять из которых, будут ложными, и пять истинными. Домашнее задание. Угринович стр.122-125.

Дата добавления: 2014-11-18