Логические законы и правила преобразования логических выражений

Законы логики отражают наиболее важные закономерности логического мышления. В алгебре высказываний законы логики записываются в виде формул.

Логические выражения называются равносильными, если их истинностные значения совпадают при любых значениях входящих в них логических переменных.

Приведём соотношения, отражающие эти законы.

1. Закон тождества: Всякое высказывание тождественно самому себе. (вывел Аристотель– основатель логики как научной дисциплины):

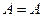
2. Закон непротиворечия: Высказывание не может быть одновременно истинным и ложным (Аристотель)

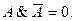
Примеры противоречивых утверждений:

1) «яблоко – спелое» и «яблоко – неспелое»;

2) «треугольник АВС – прямоугольный» и «стороны треугольника равны друг другу».

3. Закон исключительного третьего: Высказывание может быть либо истинным, либо ложным, третьего не дано. (Аристотель):

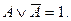
Примеры взаимоисключающих утверждений:

1) «Сегодня будет дождь» или «Сегодня дождя не будет».

2) «Любой треугольник правильный либо в нем есть разные стороны».

4. Закон двойного отрицания: Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание (Аристотель).

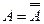
Примеры рассуждений.

1) Неверно, что «Вчера не было дождя». Следовательно, «Вчера был дождь».

2) Неправда, что «это сделал не Саша». Следовательно, «это сделал Саша».

5. Закон общей инверсии (законы де Моргана):

– для логического сложения:

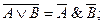
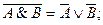
Большое значение, для выполнения преобразований логических выражений имеют законы алгебраических преобразований. Многие из них имеют аналоги в обычной алгебре.

1. Переместительный закон (закон коммутативности):

– для логического сложения:

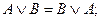
– для логического умножения:

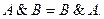
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания. В обычной алгебре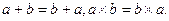

3. Сочетательный закон (закон ассоциативности):

– для логического сложения:

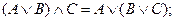
– для логического умножения:

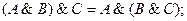
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.

В обычной алгебре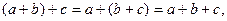

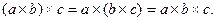
4. Распределительный закон (закон дистрибутивности):

– для логического сложения:

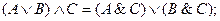
– для логического умножения:

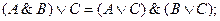
Определяет правило выноса общего высказывания за скобку.

В обычной алгебре справедлив распределительный закон только для сложения:

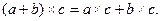
При решении задач могут быть полезны следующие правила:

5.

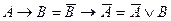
6.

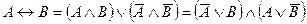
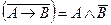
7.	12.	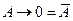17.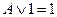
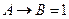
8.	13.	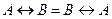18.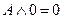
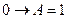
9.	14.	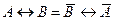19.
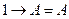
10.	15.	20.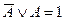
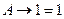
11.	16.	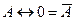21.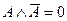

Дата добавления: 2014-11-18