Лекция 22. Расчет динамических характеристик шпиндельных узлов

Показатели динамического качества некоторых станков определяются в основном параметрами шпиндельных узлов. К таким станкам относятся, например, токарные (особенно при обработке в патроне), координатно-расточные (при работе жесткой борштангой), внутришлифовальные, расточные и др. Естественно, что вместо расчета динамических характеристик всего станка в таких случаях можно ограничиться расчетом характеристик только шпиндельного узла.

Расчет характеристик шпинделя можно вести по методике, описанной выше, т. е. рассматривать шпиндель в виде невесомой упругой балки на упругодемпфирующих опорах с некоторым количеством сосредоточенных масс.

Однако для многоопорных шпинделей или шпинделей, имеющих в одной опоре несколько подшипников, при расчете требуется выполнять раскрытие статической неопределимости. Это усложняет расчет.

Среди численных методов расчета статических и динамических характеристик шпиндельных узлов станков как линейных упругих систем получил распространение метод начальных параметров в матричной формулировке (метод переходных матриц). Рассмотрим основные положения этого метода расчета.

Шпиндель станка (рис. 18.7) рассматривают как ступенчатую балку длиной на упругих опорах с вязким демпфированием, пропорциональным скорости колебаний. Балку разбивают на N участков, разграниченных изменением диаметра (геометрического момента инерции), опорой, сосредоточенной массой, внешней сосредоточенной нагрузкой или скачком распределенной нагрузки. Каждый i-й участок имеет постоянные (в пределах участка) распределенную массу m_i и изгибную жесткость EJ_i.

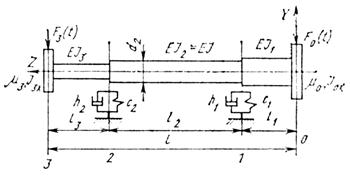
Смонтированные на шпинделе детали (шкивы, зубчатые колеса, патрон) представляют в виде сосредоточенных грузов, расположенных на границах участков и имеющих массу 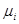и момент инерции J_ix. При составлении расчетной схемы используют общепринятые рекомендации относительно опор шпинделя, представляя их в виде линейно-упругих опор (при радиальном и угловом смещениях) с вязким демпфированием.

Расчет динамических характеристик шпиндельного узла сводится к определению амплитуд установившихся колебаний шпинделя в нулевом сечении (на переднем конце) от гармонических силовых возмущений со стороны процесса резания, привода и т. п.

Рис.18.7.Расчетнаясхема шпиндельного узла станка  

Линейная постановка задачи позволяет использовать принцип суперпозиции и последовательно определять характеристики узла при всех указанных выше воздействиях.

Рассмотрим применение метода начальных параметров для расчета динамических характеристик шпинделя, схема которого показана на

рис. 18.7. Шпиндель разбит на три участка. На концах его расположены сосредоточенные грузы (например, патрон и шкив ременной передачи). В нулевом сечении шпинделя действуют возмущения со стороны процесса резания — сила F₀ (t), в третьем сечении — возмущения от привода F₃ (t)

Обозначив в i-м сечении амплитуду перемещений через Y_i, угол поворота сечения через 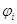; изгибающий момент через M_i и поперечную силу через Q_i можно выразить решение дифференциального уравнения колебаний шпинделя через параметры y_i, 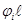, , 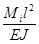напряженного и деформированного состояния на его концах (за EJ — EJ₂ принята жесткость межопорной части шпинделя; — длина шпинделя). Векторы параметров на свободных концах шпинделя (в нулевом и третьем сечениях) без учета внешней нагрузки имеют вид

;

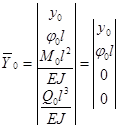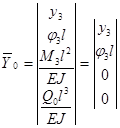
Метод позволяет связать параметры в нулевом сечении шпинделя через переходные матрицы его сечений и участков с параметрами в третьем сечении.

При колебаниях в нулевом сечении действуют сосредоточенная сила и момент инерционных сил патрона, амплитудные значения которых соответственно равны 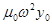и 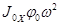- Матрица сосредоточенного груза

,

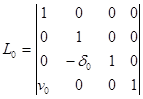Где ; ,

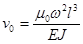преобразует параметры 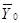при переходе через нулевое сечение. Далее идет первый участок шпинделя с распределенной массой 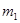и жесткостью EJ₁. Зависимость между параметрами на его концах определяется переходной матрицей участка:

,

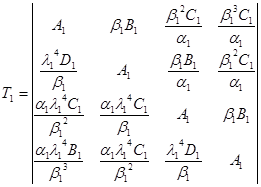Где ; ; ,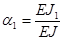

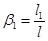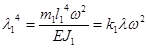а функции A₁,B₁,C₁,D₁ могут быть представлены в виде степенных рядов.

Над опорой 1 перерезывающая сила изменяется скачком на величину реакции опоры (учитываются упругая и диссипативная составляющие реакции). Этот скачок при переходе через опору учитывается умножением вектора параметров на матрицу опоры

,

где 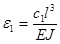; 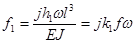( и 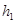) соответственно коэффициенты жесткости и демпфирования опоры; )

Переходя, таким образом, от участка к участку, доходят до левого конца шпинделя, где параметры выражены вектором . В результате получают матричные уравнения (без учета внешней нагрузки)

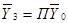, (18.11)

где переходная матрица П для схемы, приведенной на рис. 18.7, равна произведению

,

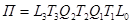где L₀ и L₃ — матрицы сосредоточенных грузов в нулевом и третьем сечениях; Т_1, Т₂ и Т₃ — матрицы 1, 2 и 3-го участков шпинделя с распределенной массой; Q₁ и Q₂ — матрицы линейно-упругих опор шпинделя с вязким демпфированием.

С учетом внешней нагрузки в нулевом и третьем сечениях уравнение (18.11) примет вид

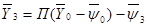, (18.12)

где

; .

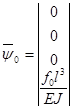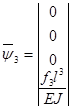Определение переходной матрицы П сводится к перемножению нескольких матриц размером 4X4. Обычно на концах шпинделя два из четырех параметров в матрицах-столбцах 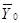и равны нулю, что позволяет существенно рационализировать вычислительную работу. Покажем это на примерах. При вычислении передаточной функции W₀ (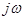) системы по воздействию со стороны процесса резания (при F₃ = 0) уравнение (18.12) в развернутом виде записывают так:

.

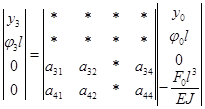Как видим, в матрице П следует из 16 сохранить только шесть элементов, которые расположены на пересечении строк, совпадающих с нулевыми строками вектора , и столбцов, совпадающих с не равными нулю строками вектора (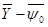) (остальные элементы, не используемые в расчетах, заменены звездочками). В результате можно записать два линейных уравнения относительно искомых параметров 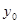и :

;

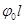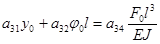, (18.13)

где коэффициенты а являются функциями частоты инерционных, диссипативных, упругих и геометрических параметров шпиндельного узла.

Непосредственно из уравнений (18.13) может быть получено выражение для частотной передаточной функции системы

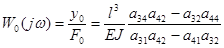. (18.14)

Аналогично определяют и частотную передаточную функцию 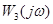системы по воздействию со стороны привода (при F₀ = 0). Опуская промежуточные выкладки, получим

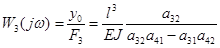. (18.15)

Вычисление элементов переходных матриц-сомножителей и их последующее умножение производится на ЭВМ. Так как некоторые элементы матриц Q₁ и Q₂ упругодемпфирующих опор являются комплексными числами, то переходная матрица-произведение 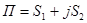также оказывается состоящей из двух матриц S₁ и S₂. Выражение для частотных передаточных функций W₀ (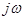) или W₃ (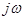) приводят к виду

(18.16)

используя для определения Р₁, Р₂, Р₃ и Р₄ элементы матриц S₁ и S₂.

После разделения действительной и мнимой частей выражения (18.16) получают возможность определения составляющих 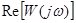и амплитудно-фазовой частотной характеристики динамической системы шпиндельного узла.

Дата добавления: 2014-11-18