Подобие в лопастных насосах

При проектировании и испытаниях насосов широко используется теория подобия. Например, используется геометрически подобные модели, характеристики которых хорошо известны, можем предсказать подобные характеристики вновь проектируемого насоса или, получив характеристики насоса на одном режиме работы, можем получить при помощи расчетов для других режимов работы.

Критерии подобия – безразмерные алгебраические выражения, состоящие из отдельных параметров и характеризующие подобие явлений или машин. Равенство критериев подобия означает подобие явлений или машин.

Явления называются подобными, если процессы в них имеют одинаковую физическую природу, а отношение сходственных величин в сходственные моменты времени одинаковы.

Процесс достижения подобия явлений или машин называется моделированием. Основой моделирования является геометрическое, кинематическое и динамическое подобие.

Геометрическое подобие означает постоянство отношений всех сходственных величин (линейных размеров) у модели и натуры.

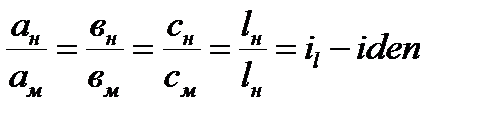(const)

Для геометрически подобных насосов можно записать так:

,

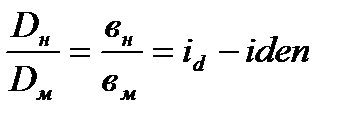где:

а_н, в_н,.с_н, l_н D_н – линейные размеры натурного объекта;

а_м, в_м,.с_м l_м D_м – линейные размеры модельного объекта.

При этом у модели и натуры должно быть постоянство сходственных углов.

Кинематическое подобие означает постоянство всех сходственных скоростей у модели и натуры, а также постоянство углов между векторами этих скоростей.

U_2н, V_2н,.W_2н, V_2uн, V_2mн – окружная, абсолютная, относительная, тангенциальная, меридианная скорости на выходе из колеса натурного насоса;

U_2м, V_2м,.W_2м, V_2uм, V_2mм – окружная, абсолютная, относительная, тангенциальная, меридианная скорости на выходе из колеса модельного насоса.

Динамическое подобие означает постоянство отношений сил инерции к силам тяжести или трения.

Основными критериями подобия являются:

1. критерий Фруда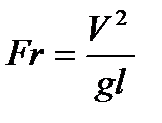

2. критерий Рейнольдса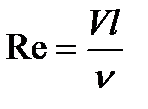

3. критерий Струхаля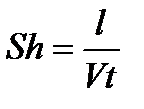

4. критерий Эйлера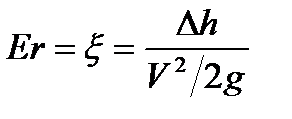

Размеры модели и расход через модель подбирают таким образом, чтобы течение проходило в автомодельной области. При этом отличие в значениях критерия Рейнольдса не будет оказывать существенное влияние на процессы течения жидкости. Течение в насосах напорное, поэтому критерий Фруда не оказывает влияния на процесс течения Равенство критериев Струхаля будет выполнено, если у модели и натуры соблюдается кинематическое подобие. Таким образом, главными факторами моделирования процессов в насосах будут:

1. геометрическое подобие

2. кинематическое подобие

3. критерий Рейнольдца должен быть таким, чтобы течение проходило в автомодельной области.

Основные законы подобия лопастных насосов.

Пусть два насоса геометрически подобны. Подберем режимы их работы (Q,n) так, чтобы режимы течения жидкости в них были кинематически подобны, т.е. мноугольники скоростей у натуры и модели были подобны.

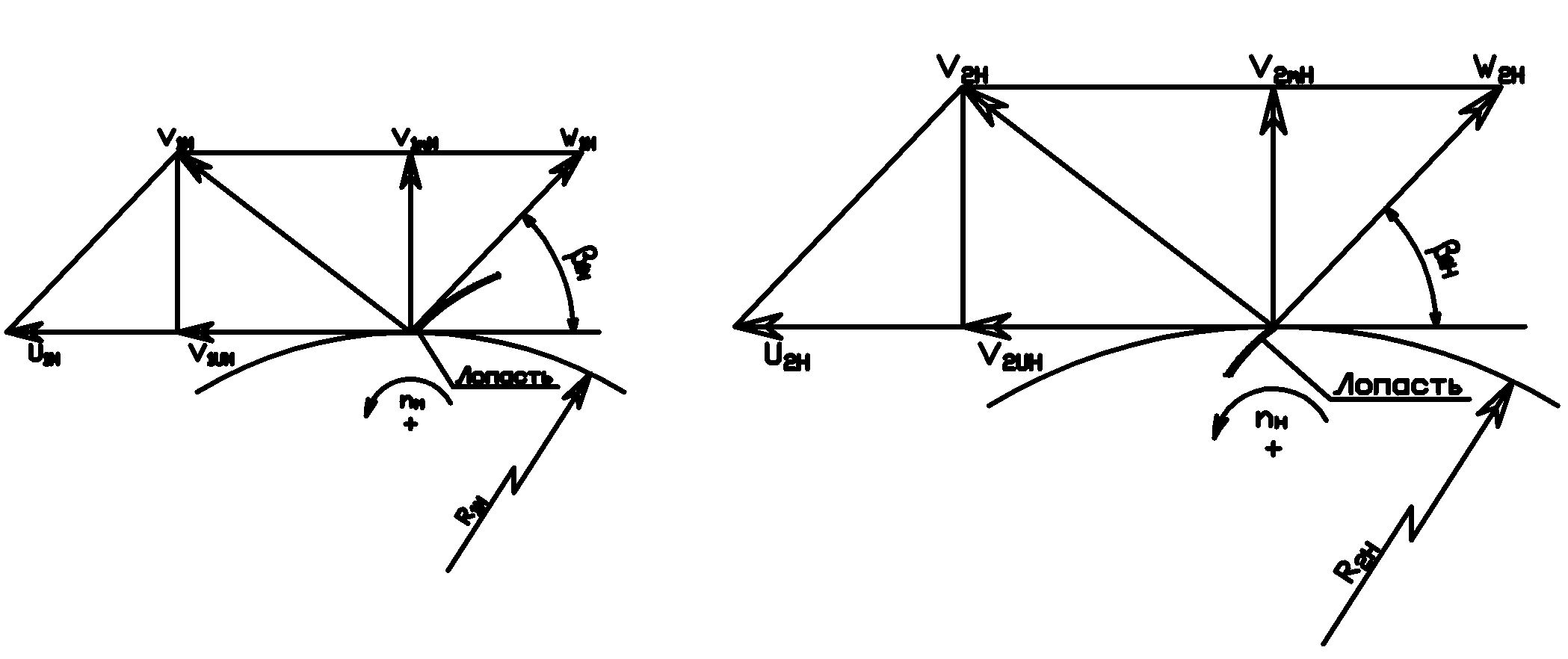
Из подобия мноугольников скоростей натуры и модели имеем:

,

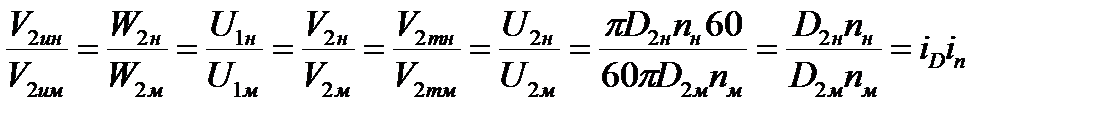где:

D_2н, D_2м – соответственно внешний диаметр колеса у натурного и модельного насоса;

n_н, n_м – соответственно частота вращения у натурного и модельного насоса;

i_D, i_n – соответственно коэффициенты (масштабы) геометрического моделирования и моделирования частоты вращения.

Можно записать:

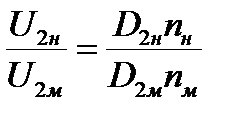
или

,

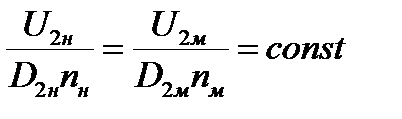аналогично для других скоростей.

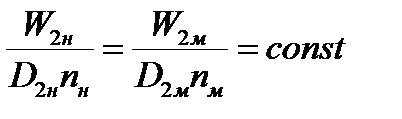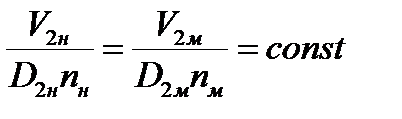, , и.т.д.

Эти выражения будут справедливы для всего множества подобных насосов, поэтому индексы натуры и модели можно не указывать:

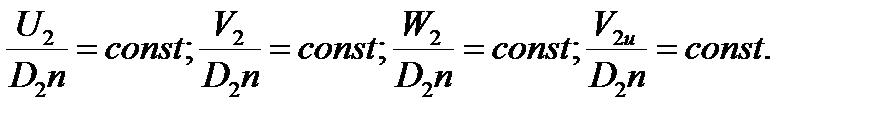
- - 1 закон подобия лопастных

насосов

Возьмем отношение подач этих насосов:

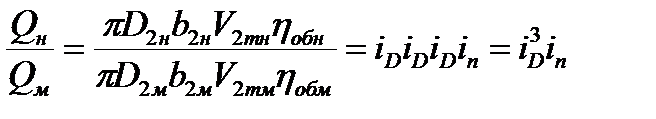
Все зазоры между подвижными и неподвижными частями насоса изменяются пропорционально изменению размеров насоса, соответственно также изменяется

подача и утечки в насосе, поэтому можно принять что объемный КПД насоса

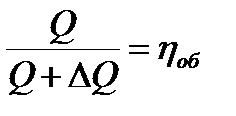
(, ∆Q – утечки) меняются мало, т.е. η_{об н} ≈ η_{об м}.

Таким образом

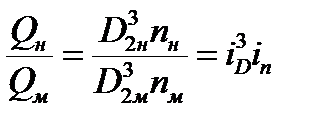или

,

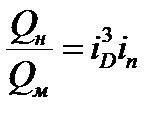так как

,

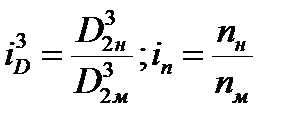то можно записать

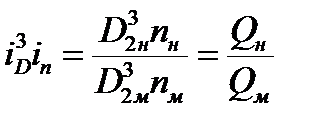
Представим последнее выражение в следующем виде:

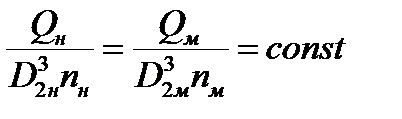
Эти выражения будут справедливо для всего множества подобных насосов, поэтому индексы натуры и модели можно не указывать:

- 2 закон подобия лопастных насосов

Возьмем отношение напоров этих насосов:

Если считать, что для геометрически подобных насосов относительная

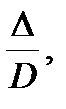шероховатость (, где ∆ - абсолютная шероховатось) у модели и натуры примерно одинакова, тогда можно принять что η_{гн ≈} η_гм.

,

т.к.

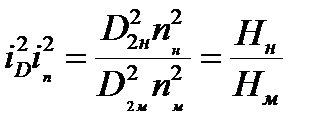
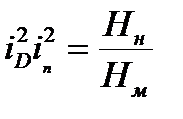
Эти выражения будут справедливо для всего множества подобных насосов, поэтому индексы натуры и модели можно не указывать:

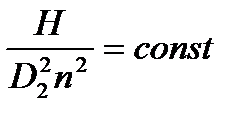
- 3 закон подобия лопастных насосов

Возьмем отношение мощностей этих насосов, учитывая при этом, что:

, ,

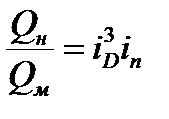Можно принять η_н ≈ η_м

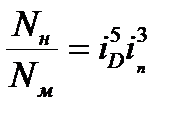
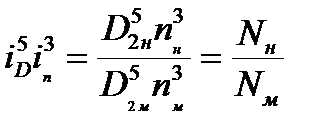
или

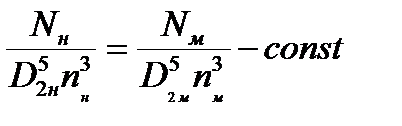
Эти выражения будут справедливо для всего множества подобных насосов, поэтому индексы натуры и модели можно не указывать:

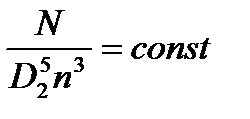
- 4 закон подобия лопастных насосов

Вывод: Для геометрически подобных насосов при кинематически подобных режимах сохраняется постоянство критериев подобия.

Частный случай: если модель и натура один и то же насос, меняется только Q и n, то для кинематически подобных режимов, т.е. D_2н = D_2м:

Так как то:

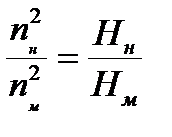
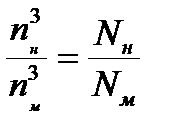
Делая преобразования аналогичные приведенным выше получим:

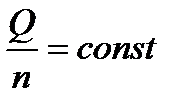
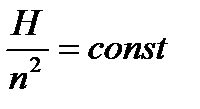
Обозначим:

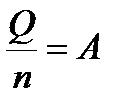
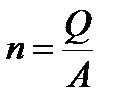
Выразим

Подставим

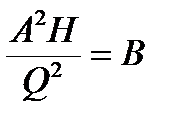
Отсюда

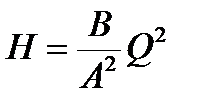
Обозначим

Получим

- это уравнение параболы

Таким образом, для любой постоянной частоты вращениякинематически подобные

режимы расположены на пораболах, проведенных из начала коодинат

После ряда преобразований получим формулы пересчетом характеристик насоса с одной частоты на другую частоту вращения:

, ,

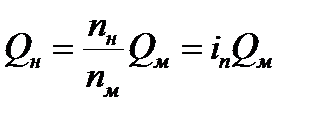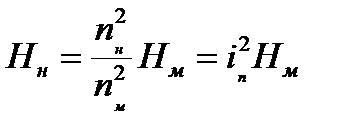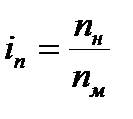
Практическое использование тории подобия:

1. зная опытные характеристики насоса, можно изготовить новый насос (модель) больших или меньших размеров и получить путем пересчета характеристики этого насоса.

2. имея опытные характеристики насоса на одной частоте вращения, можно путем пересчета получить аналогичные характеристики для других частот вращения.

Коэффициент быстроходности насоса

Исходные уравнения (см. раздел подобие лопастных насосов):

;

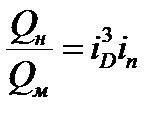Возведем левую и правую часть второго уравнения в степень 3/2

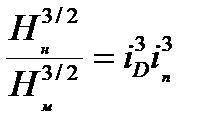
Отсюда:

Подставим 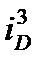в первое уравнение

Выразим

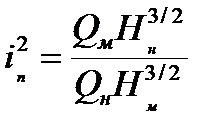
Так как , то

, тогда

Было принято решение считать у модельного насоса H_м=1м., Q_м=0,075м³/с, тогда

1.

Обозначив n_м = n_s получим

- Коффициент быстроходности насоса

n_s - быстроходность насоса это частота вращения воображаемого модельного насоса, у которого H = 1м., Q = 0,075м³/с, геометрически подобного натурному.

Для насосов типа Д - Q = 1/2Q_opt

Для многоступенчатых[насосов – H = H_opt/i_ст, где i_ст – число ступений насоса.

Q_opt, H_opt – соответственно подача (м³/с) и напор (м) насоса для режима максимального КПД.

n_s – можно считать критерием подобия. Он позволяет определять:

- примерную форму рабочего колеса насоса (лопасти);

- примерное отношение D₂/ D_о;

- примерну форму характеристик насоса H, N, η, ∆h =f(Q) при n_s – const.

Классификация насосов по быстроходности.

Форма рабочих колес в зависимости от n_s.

Характеристика сети (трубопровода) и подача насоса.

Характеристика трубопровода выражается следующим уравнением:

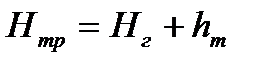, где

Н_г – геодезическая высота подъема;

h_т – потери напора во всасывающей и напорной линии насосной установки.

, где

h_тм – местные потери напора;

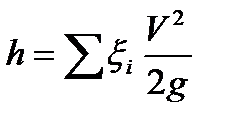, где

x - коэффициент сопротивления.

h_тдл – потери напора по длине.

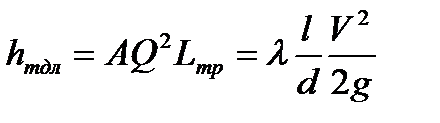, где

А – удельное сопротивление;

l - зависит от числа Re;

l – длина трубопровода.

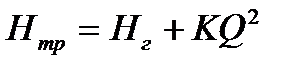
Точка пересечения Н_тр-Q и Н-Q – рабочая точка. Рабочая точка зависит только от характеристики трубопровода и должна лежать в пределах рабочей зоны насоса.

Регулирование подачи лопастных насосов.

Задача – изменять подачу воды потребителю или поддерживать ее постоянной при изменении характеристики трубопроводной сети (Н_г).

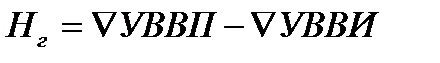
1. Количественный способ – изменение характеристики трубопровода при неизменной характеристике насоса. Прикрывая задвижку на напоре увеличиваем потери в трубопроводе (К – возрастает), как следствие, крутизну характеристики Н_тр-Q, а значит смещаем рабочую точку влево, в область меньших подач.

Пусть подача задана

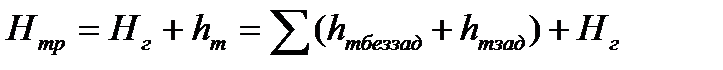
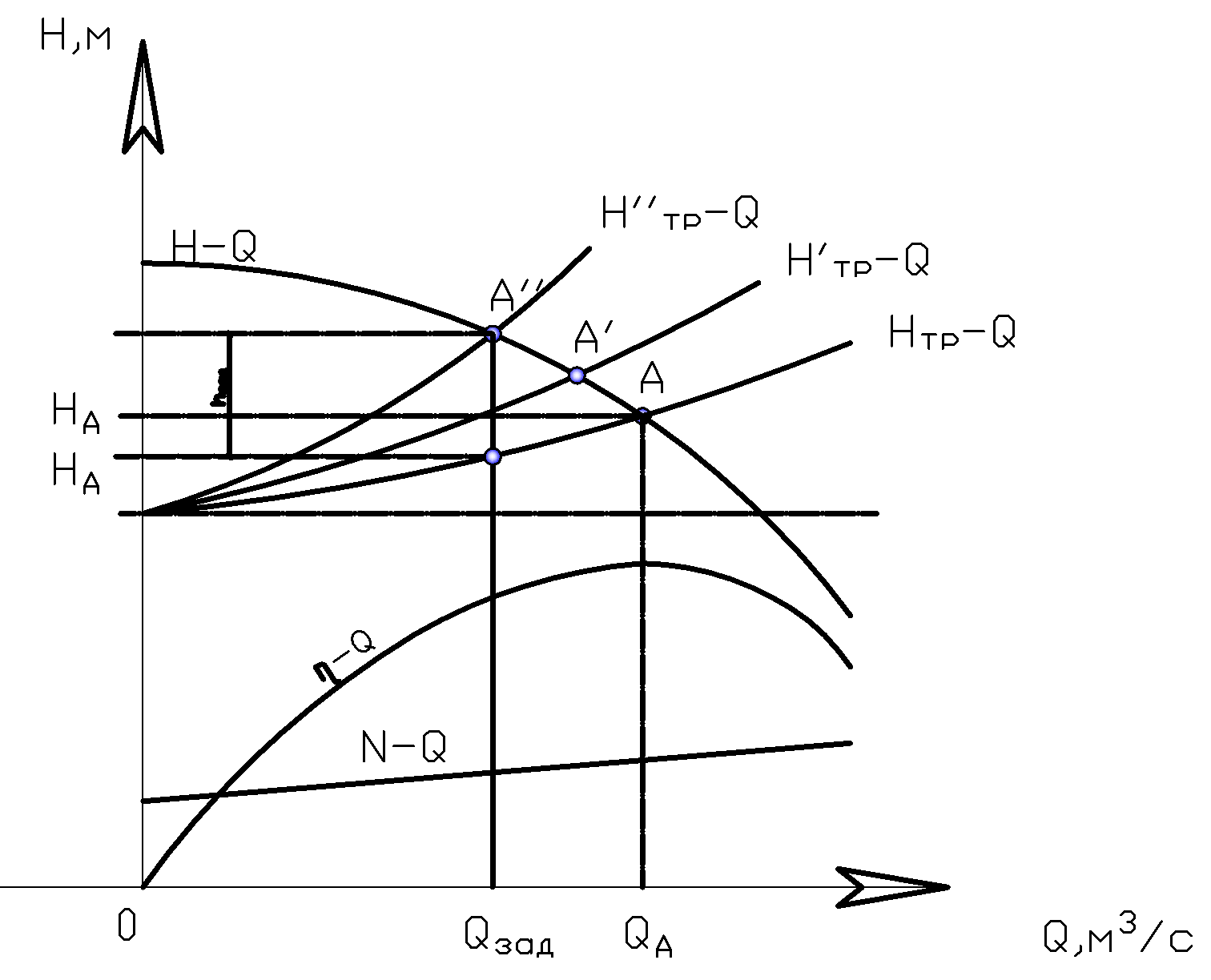
Особенности:

4. применяется только снижения подачи ;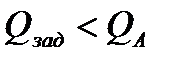

5. экономичность насосной установки снижается, т.к. увеличиваются потери на задвижке.

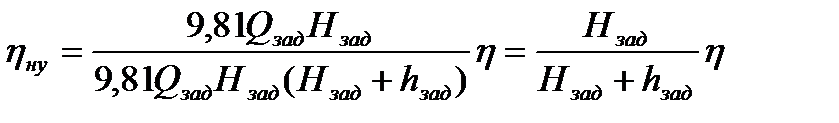
4. наиболее рационально применять этот способ при пологих характеристиках Н_тр – Q и Н – Q, т.к. потери в задвижке будут малы.

5. на практике применяется только на небольших насосных установках.

2. Качественный способ регулирования.

Изменяют характеристику насоса Н – Q при неизменной характеристике сети Н_тр – Q. Характеристика насоса изменяется за счет изменения n. Ее изменяют так, чтобы при новой n насос подавал заданную подачу.

Порядок нахождения неизвестной частоты вращения.

1.

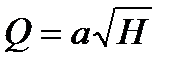
2. N – Q

3. H – Q

4. H_тр – Q

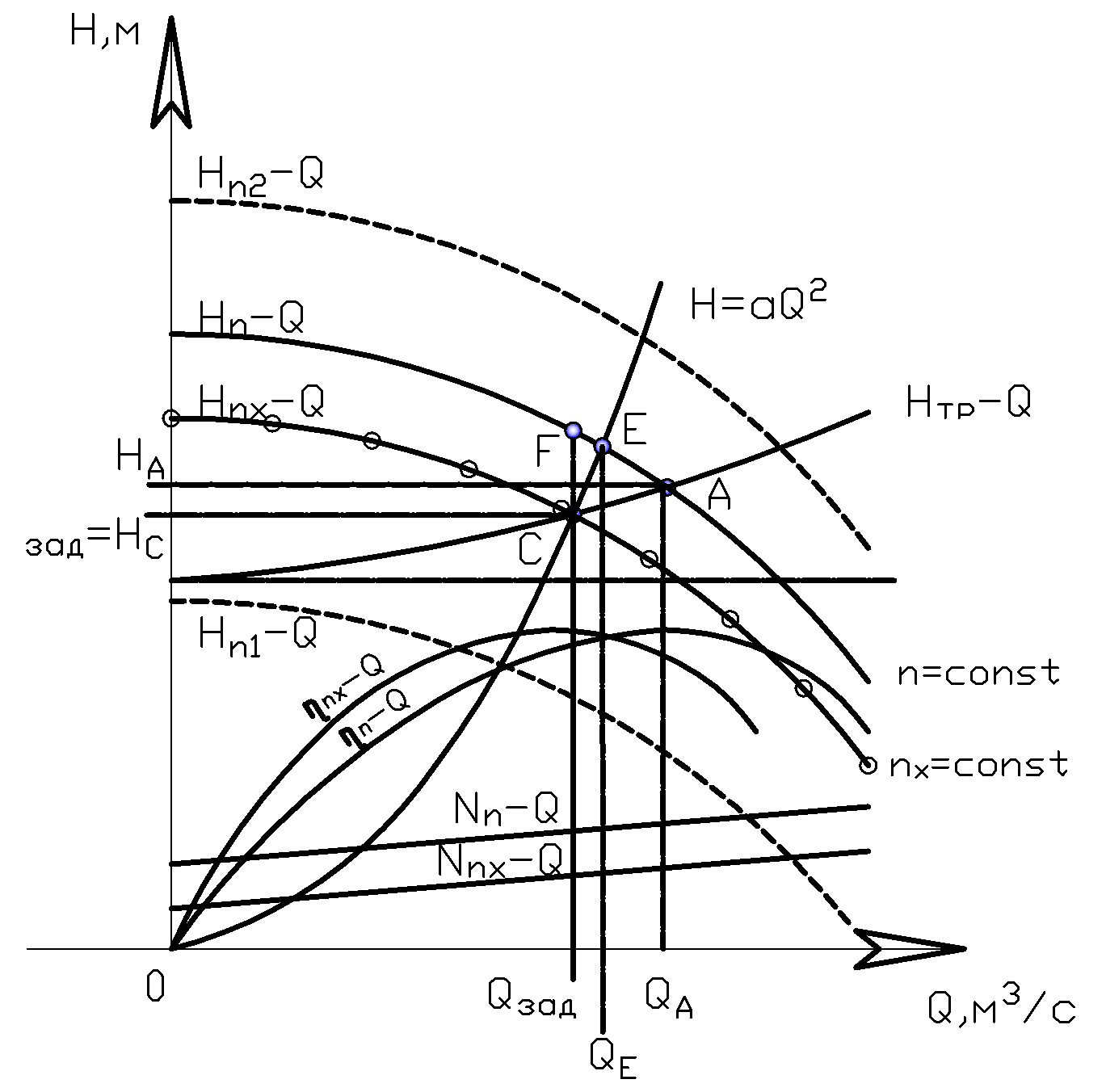
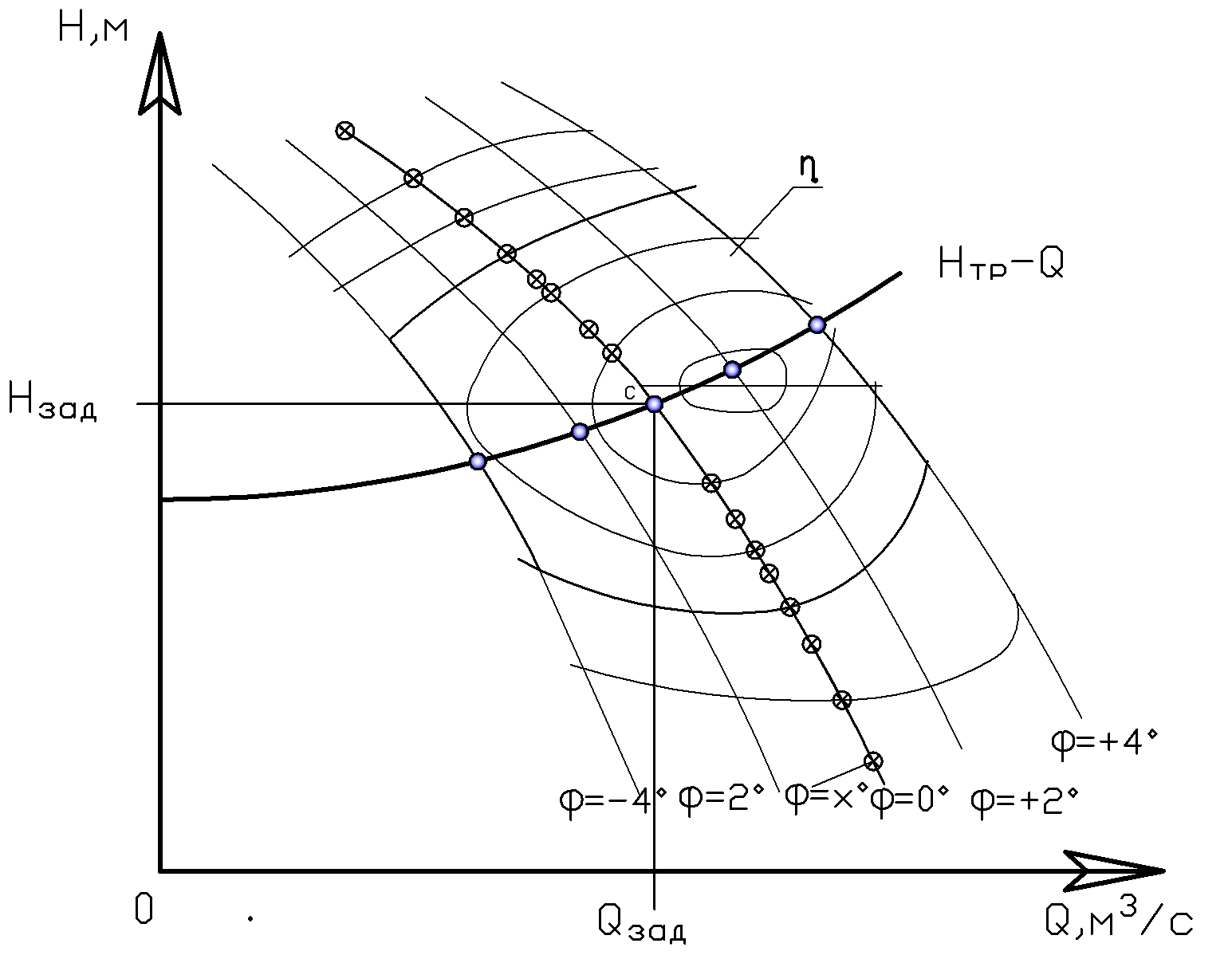
1. строится парабола – кривая подобных режимов. Точка С – заданная точка.

2. находим параметры точки Е – Q_е и Н_е.

3. определяем искомую (новую) частоту вращения по закону динамического подобия:

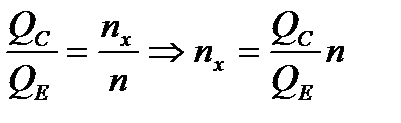. Точки С и Е – подобные, т.к. лежат на кривой подобия.

.

4. задаемся несколькими точками на оси абсцисс на исходной характеристики насоса и по закону динамического подобия пересчитываем характеристики насоса.

КПД насоса при изменении частоты вращения не меняется, но кривая будет другой, т.к. меняется Q.

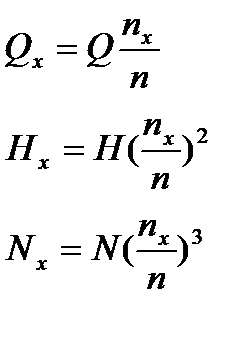
Особенности этого способа регулирования:

1. может использоваться как и для увеличения, так и для уменьшения подачи;

2. не приводит к снижению экономичности, т.к. нет потерь в прикрытой задвижке;

3. необходимо иметь двигатель с регулируемой частотой вращения (двигатель постоянного тока, при двигателе переменного тока необходимы преобразователи частоты тока, что дорого, либо гидромуфту или электромуфту, а также вариатор, но все это дорого).

Регулирование подачи при помощи поворота лопастей рабочего колеса (у осевых насосов).

Изменяя угол установки лопастей, мы меняем характеристики насоса, а значит меняем местоположение рабочей точки.

По существу это качественный способ регулирования (отсутствуют потери в прикрытой задвижке). Угол установки лопастей определяем интерполированием.

Особенности:

- применяется только у осевых и диагональных насосов;

- сложность конструкции привода разворота лопастей.

Параллельная работа нескольких насосов на один трубопровод.

Применяются для увеличения расхода по одному трубопроводу. Потери в двух трубопроводах одинаковы. В точке А давление общее для обоих насосов. Это означает, что на участке от уровня воды до точки А потери равны, а следовательно потери у насосов одинаковы.

Общая характеристика работающих насосов строится путем сложения подач насосов при произвольных, но равных напорах.

Н_1,2 – Q – общая характеристика.

Точки А₁, А₂ – рабочие точки насосов, работающих отдельно на трубопровод.

Точки - рабочие точки насосов, работающих совместно на трубопровод.

Точка А_1,2 – общая рабочая точка.

Q_1,2 – общая подача

При работе этих же насосов каждый на свой трубопровод общая подача составит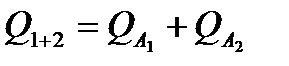

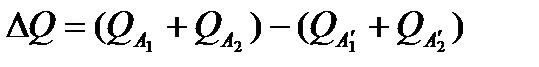- дефицит подачи.

Если подавать воду двумя насосами по двум трубопроводам, то суммарная подача их больше на величину DQ, чем при работе обоих насосов на один и тот же трубопровод.

Дата добавления: 2014-11-20