
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обтекании труб и пучков
|
|
|
|
Расчетные формулы по теплоотдаче при поперечном
ЖИДКОСТИ
ТЕПЛООТДАЧА ПРИ ВЫНУЖДЕННОМ ДВИЖЕНИИ
В следующих формулах (146) — (159) определяющие величины - наружный диаметр трубок (проволоки) и средняя температура жидкости (кроме 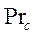 ); скорость потока подсчитывается по самому узкому поперечному сечению канала (пучка);
); скорость потока подсчитывается по самому узкому поперечному сечению канала (пучка); 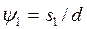 и
и 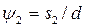 — относительные поперечный и продольный шаги.
— относительные поперечный и продольный шаги.
А. Одиночная труба. Для одиночной круглой трубы средняя теплоотдача при нагревании жидкости определяется следующими формулами
при 
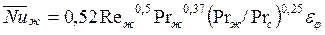 ; (146)
; (146)
при 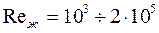
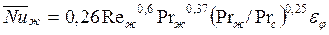 ; (147)
; (147)
при 
 . (148)
. (148)
Для тонкой проволоки и круглой трубы в потоке трансформаторного масла при  имеем
имеем
 . (149)
. (149)
При охлаждении жидкости показатель степени отношения  вместо 0,25 принимается равным 0,2. Для газов поправка
вместо 0,25 принимается равным 0,2. Для газов поправка 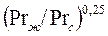 не имеет смысла. Поправка на влияние угла атаки
не имеет смысла. Поправка на влияние угла атаки  при обтекании труб под углом
при обтекании труб под углом 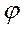 находится по рис. 11.
находится по рис. 11.
Б. Трубные пучки с гладкой поверхностью. Средняя теплоотдача для труб, расположенных в глубинном ряду шахматного пучка (рис. 12):
при  и
и 
 ; (150)
; (150)
при  и
и 
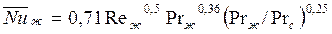 ; (151)
; (151)
при 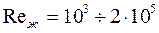 ,
,  ,
, 
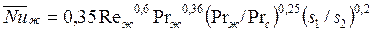 при
при  (152)
(152)
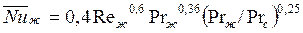 при
при 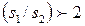 (153)
(153)
при  ,
, 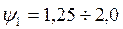 ,
, 
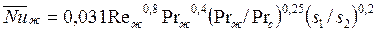 . (154)
. (154)
Для коридорных пучков (рис. 12):
при  и
и 
 ; (155)
; (155)
при 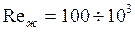 и
и 
 ; (156)
; (156)
при 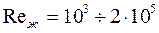 ,
, 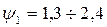 и
и 
 ; (157)
; (157)
при  ,
, 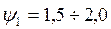 и
и 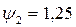
 . (158)
. (158)
При обтекании шахматных и коридорных пучков жидкими металлами
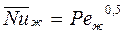 . (159)
. (159)
Формула применяется при  ,
,  ,
,  ,
,  .
.
Средняя теплоотдача всего пучка гладких труб
 , (160) где
, (160) где  — средняя теплоотдача трубы в глубинном ряду пучка при
— средняя теплоотдача трубы в глубинном ряду пучка при  , определяется по формулам (150)—(159);
, определяется по формулам (150)—(159);  — поправка на влияние угла атаки, находится по рис. 13;
— поправка на влияние угла атаки, находится по рис. 13;  — поправка, учитывающая зависимость теплоотдачи от числа z рядов труб в пучке, определяется по рис. 14.
— поправка, учитывающая зависимость теплоотдачи от числа z рядов труб в пучке, определяется по рис. 14.
В. Трубные пучки из оребренных труб. Для пучков из труб с круглыми ребрами коэффициент теплоотдачи с оребренной стороны (рис. 15) определяется формулой
 , (161) где
, (161) где 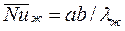 ;
;  ;
; 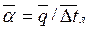 отнесен к полной поверхности оребренных труб.
отнесен к полной поверхности оребренных труб.
Скорость газа  находится по узкому сечению
находится по узкому сечению
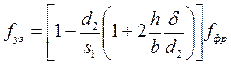 , (162)
, (162)
где  — толщина ребра;
— толщина ребра; 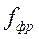 — площадь фронтального сечения теплообменника;
— площадь фронтального сечения теплообменника;  — поперечный шаг труб; h— высота ребра; b— шаг ребер.
— поперечный шаг труб; h— высота ребра; b— шаг ребер.
Неравномерность теплоотдачи по высоте ребра учитывается коэффициентом 
При коридорном расположении оребренных труб в формуле (161) принимается С=0,105, n=0,72. Количество поперечных рядов z в пучке учитывается  : при n=1, 2, 3, 4 и более
: при n=1, 2, 3, 4 и более  =1,6; 1,3; 1,1; 1,0 соответственно. Расположение труб в пучке учитывается
=1,6; 1,3; 1,1; 1,0 соответственно. Расположение труб в пучке учитывается 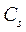 : при
: при  1,4; 1,7; 2 и более коэффициент
1,4; 1,7; 2 и более коэффициент  =0,85; 0,96; 1,0 соответственно (
=0,85; 0,96; 1,0 соответственно ( - продольный шаг труб). Формула (161) справедлива при
- продольный шаг труб). Формула (161) справедлива при 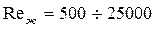 ,
,  ,
,  .
.
При шахматном расположении оребренных труб в формуле (161) принимается С=0,23; n=0,65. Коэффициент
 , (163) где
, (163) где  - диагональный шаг труб в пучке.
- диагональный шаг труб в пучке.
Коэффициент  представлен ниже:
представлен ниже:
z ………… 1 4 6 8 10 16 20
 ………… 0,8 0,95 0,98 0,99 1,0 1,015 1,025
………… 0,8 0,95 0,98 0,99 1,0 1,015 1,025
Формула (161) справедлива при  ,
,  ,
,  ,
, 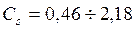 .
.
Свойства потока газа 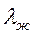 ,
, 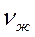 определяются по его средней температуре
определяются по его средней температуре 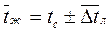 .
.
Коэффициент теплопередачи через ребристую стенку
 , (164) где
, (164) где  — приведенный коэффициент теплоотдачи снаружи оребренной поверхности;
— приведенный коэффициент теплоотдачи снаружи оребренной поверхности; 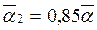 — коэффициент теплоотдачи со стороны оребренной поверхности,
— коэффициент теплоотдачи со стороны оребренной поверхности, 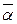 находится по формуле (161);
находится по формуле (161); 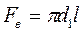 — площадь внутренней поверхности несущей трубки;
— площадь внутренней поверхности несущей трубки;  площадь полной наружной поверхности оребренной трубки вместе с поверхностью ребер;
площадь полной наружной поверхности оребренной трубки вместе с поверхностью ребер;  - коэффициент эффективности круглого ребра постоянной толщины, определяется из графика рис. П.8 Приложения;
- коэффициент эффективности круглого ребра постоянной толщины, определяется из графика рис. П.8 Приложения; 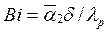 — число Био,
— число Био, 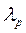 — теплопроводность материала ребра;
— теплопроводность материала ребра;  ,
,  — площади поверхности ребер и стенки трубы в промежутках между ребрами;
— площади поверхности ребер и стенки трубы в промежутках между ребрами;  —толщина стенки;
—толщина стенки;  - теплопроводность материала стенки.
- теплопроводность материала стенки.
Тепловой поток через ребристую стенку при постоянных температурах обеих жидкостей 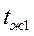 и
и 
 , (165)
, (165)
где  — полная оребренная поверхность теплообмена всего пучка труб.
— полная оребренная поверхность теплообмена всего пучка труб.
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 947; Нарушение авторских прав?; Мы поможем в написании вашей работы!