
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция №14
|
|
|
|
Теплоотдача при движении потока внутри труб (каналов)
ЖИДКОСТИ
ТЕПЛООТДАЧА ПРИ ВЫНУЖДЕННОМ ДВИЖЕНИИ
Лекция №13
На начальном участке круглой трубы происходит формирование гидродинамического и теплового пограничных слоев, т. е. толщина по граничных слоев увеличивается до тех пор, пока они не заполнят все поперечное сечение трубы.
Эти начальные участки называются соответственно гидродинамическим (длина 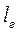 ) и тепловым (длина l т) начальными участками и характеризуются падением теплоотдачи по мере развития пограничных слоев. После начального участка течение жидкости и теплообмен стабилизируются, поле скоростей и теплоотдача становятся одинаковыми для всех поперечных сечений. Следовательно, для длинных труб при
) и тепловым (длина l т) начальными участками и характеризуются падением теплоотдачи по мере развития пограничных слоев. После начального участка течение жидкости и теплообмен стабилизируются, поле скоростей и теплоотдача становятся одинаковыми для всех поперечных сечений. Следовательно, для длинных труб при 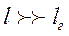 и
и 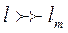 средняя теплоотдача определяется по числу
средняя теплоотдача определяется по числу 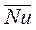 , характеризующему теплоотдачу при полностью стабилизировавшемся потоке. Для коротких труб теплоотдача выше по сравнению с длинными трубами в равных условиях.
, характеризующему теплоотдачу при полностью стабилизировавшемся потоке. Для коротких труб теплоотдача выше по сравнению с длинными трубами в равных условиях.
| Форма поперечного сечения канала | Эквивалентный диаметр | Коэффициент 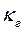
| Коэффициент 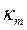
| |
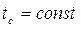
| 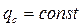
| |||
Круглое сечение, 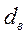 -внутнний диаметр -внутнний диаметр
| 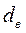
| 0,065 | 0,055 | 0,07 |
Кольцевое сечение, отношение внутреннего диаметра к наружному, 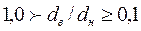
| 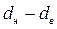
| 0,010—0,015 | 0,05 | 0,06 |
Прямоугольное сечение со сторонами а и b, 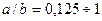
| 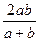
| 0,023—0,075 | — | — |
Длина начальных участков гидродинамической и тепловой стабилизации определяется по формулам
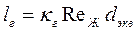 и
и 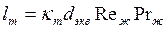 , (120) где
, (120) где 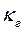 и
и 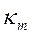 — коэффициенты, зависящие от формы канала (см. таблицу);
— коэффициенты, зависящие от формы канала (см. таблицу); 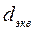 — эквивалентный диаметр сечения канала, определяется по площади f и периметру П поперечного сечения канала:
— эквивалентный диаметр сечения канала, определяется по площади f и периметру П поперечного сечения канала:
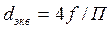 . (121)
. (121)
Следует отметить, что использование 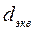 дает удовлетворительные результаты только при развитом турбулентном движении среды в каналах без острых углов.
дает удовлетворительные результаты только при развитом турбулентном движении среды в каналах без острых углов.
А. Ламинарный режим течения в круглых трубах (Rеж<2000) при отсутствии свободной конвекции называется вязкостным, а при наличии свободной конвекции — вязкостно-гравитационным. Переход одного режима в другой определяется величиной 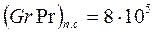 , которая находится по определяющей температуре пограничного слоя
, которая находится по определяющей температуре пограничного слоя 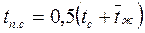 .
.
Для вязкостного режима движения при 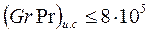 среднее по длине трубы число Нуссельта при
среднее по длине трубы число Нуссельта при 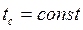
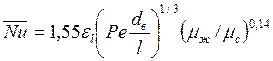 , (122) где l и
, (122) где l и 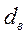 — длина и внутренний диаметр трубы.
— длина и внутренний диаметр трубы.
Формула (122) справедлива при 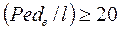 и при отношении коэффициентов динамических вязкостей
и при отношении коэффициентов динамических вязкостей 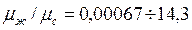 . Множитель
. Множитель 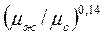 используется только для капельных жидкостей. Определяющий размер — внутренний диаметр трубы. Определяющая температура для Gr, Рr,
используется только для капельных жидкостей. Определяющий размер — внутренний диаметр трубы. Определяющая температура для Gr, Рr,  , Ре,
, Ре, 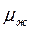 принимается
принимается 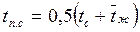 , и в Gr вводится
, и в Gr вводится 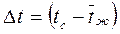 , если температура жидкости мало изменяется по длине. В противном случае определяющей температурой для
, если температура жидкости мало изменяется по длине. В противном случае определяющей температурой для 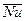 ,
,  ,
, 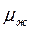 принимают
принимают 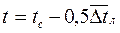 , где среднелогарифмический температурный напор
, где среднелогарифмический температурный напор 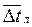 находится по формуле (95) при средней температуре стенки
находится по формуле (95) при средней температуре стенки 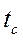 . При этом для Gr и Рr физические свойства жидкости выбираются по
. При этом для Gr и Рr физические свойства жидкости выбираются по 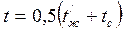 , а
, а 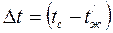 . Поправка
. Поправка 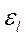 на гидродинамический начальный участок определяется по формуле
на гидродинамический начальный участок определяется по формуле
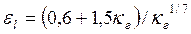 , которая справедлива при
, которая справедлива при 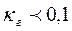 . Если
. Если 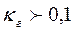 , то
, то 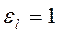 .
.
Для вязкостно-гравитационного режима при  в горизонтальных трубах длиной I справедлива формула
в горизонтальных трубах длиной I справедлива формула
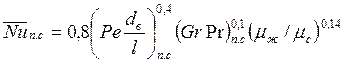 . (123)
. (123)
Формула (123) справедлива при 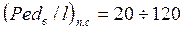 ;
; 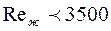 ;
; 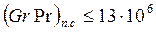 ;
; 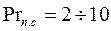 .
.
В вертикальных трубах при совпадении направлений вынужденной и свободной конвекции у стенки средняя теплоотдача определяется формулой
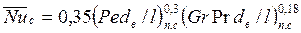 ; (124)
; (124)
здесь  ;
; 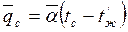 .
.
Формула справедлива при 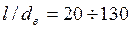 ;
;
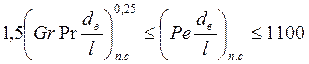 ;
; 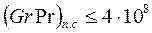 .
.
В вертикальных трубах при противоположных направлениях вынужденной и свободной конвекции у стенки средняя теплоотдача определяется формулой
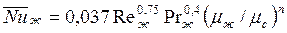 , (125) где n=0,11 при нагревании, n=0,25 при охлаждении жидкости. Формула справедлива при
, (125) где n=0,11 при нагревании, n=0,25 при охлаждении жидкости. Формула справедлива при 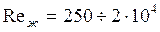 и
и 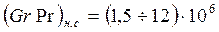 .
.
На участке стабилизированного теплообмена теплоотдача для жидкого металла определяется соотношением
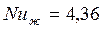 при
при 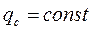 . (126)
. (126)
Б .При турбулентном течении жидкости в прямых трубах и каналах с различной формой поперечного сечения 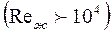 справедлива формула М. А. Михеева
справедлива формула М. А. Михеева
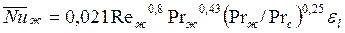 . (127)
. (127)
Для двухатомных газов (например, воздуха) при постоянных физических свойствах можно использовать формулу
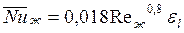 . (128)
. (128)
Коэффициент теплоотдачи 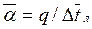 , где
, где 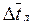 определяется по формуле (95). Определяющий геометрический размер для круглых труб — внутренний диаметр, для некруглых каналов — эквивалентный диаметр
определяется по формуле (95). Определяющий геометрический размер для круглых труб — внутренний диаметр, для некруглых каналов — эквивалентный диаметр 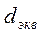 , который находится по формуле (121). Формула (127) справедлива при
, который находится по формуле (121). Формула (127) справедлива при 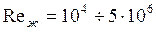 и
и 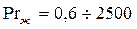 . Коэффициент
. Коэффициент 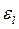 учитывает влияние начального теплового участка: при
учитывает влияние начального теплового участка: при 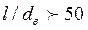
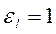 ; при
; при 
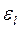 определяется из табл. 9 приложения. Номограмма для расчета по формуле (127) приведена на рис. П.7 Приложения.
определяется из табл. 9 приложения. Номограмма для расчета по формуле (127) приведена на рис. П.7 Приложения.
Для стабилизированной теплоотдачи при переменных физических свойствах жидкости рекомендуется формула (предложена Б. С. Петуховым с сотрудниками)
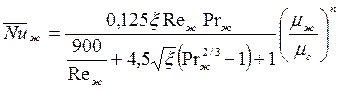 , (129) где n=0,11 при нагревании, n=0,25 при охлаждении жидкости;
, (129) где n=0,11 при нагревании, n=0,25 при охлаждении жидкости; 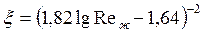 — коэффициент гидравлического сопротивления для гладких труб. Формула справедлива при
— коэффициент гидравлического сопротивления для гладких труб. Формула справедлива при 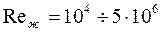 ;
; 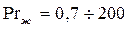 ;
; 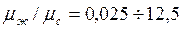 . Определяющий размер — внутренний диаметр трубы.
. Определяющий размер — внутренний диаметр трубы.
Отношение динамических вязкостей 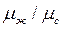 используется только для капельных жидкостей.
используется только для капельных жидкостей.
Теплоотдачу с учетом изменения физических свойств газа при турбинном течении в трубах и каналах рассчитывают по формулам:
при нагревании
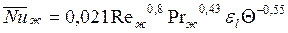 , (130) если
, (130) если 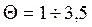 ;
;
при охлаждении
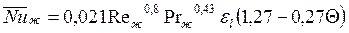 , (131) если
, (131) если 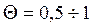 .
.
Температурный фактор
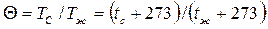 . (132)
. (132)
Определяющий размер — внутренний диаметр трубы (эквивалентный диаметр 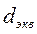 ).
).
При течении чистых жидких металлов в круглой трубе и 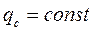 средняя теплоотдача определяется формулой
средняя теплоотдача определяется формулой
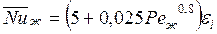 ; (133) при
; (133) при 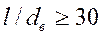
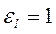 ; при
; при 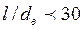
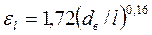 .
.
Формула (133) используется при 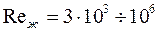 ,
, 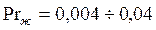 .
.
В кольцевых каналах с наружным 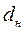 и внутренним
и внутренним 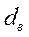 диаметрами для турбулентного стабилизированного течения теплоотдача на внутренней стенке (наружная теплоизолирована) определяется формулой
диаметрами для турбулентного стабилизированного течения теплоотдача на внутренней стенке (наружная теплоизолирована) определяется формулой
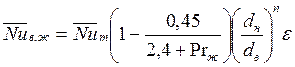 , (134) где
, (134) где 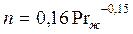 ;
; 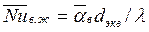 ;
; 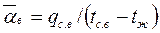 ,
, 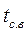 — температура на внутренней поверхности стенки. гу
— температура на внутренней поверхности стенки. гу
Теплоотдача на наружной стенке (внутренняя теплоизолирована) определяется формулой
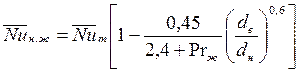 , (135) где
, (135) где 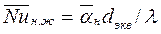 ;
; 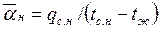 ;
; 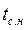 — температура на наружной поверхности стенки.
— температура на наружной поверхности стенки.
В формулах (134) и (135) 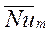 — число Нуссельта, вычисленное по формуле (127) с эквивалентным диаметром
— число Нуссельта, вычисленное по формуле (127) с эквивалентным диаметром 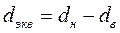 . Поправочный коэффициент
. Поправочный коэффициент 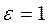 , если
, если 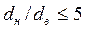 , и
, и 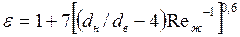 , если
, если 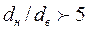 . Формулы (134) и (135) справедливы при
. Формулы (134) и (135) справедливы при 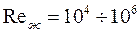 ,
, 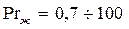 и
и 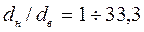 .
.
Для определения длины участка тепловой стабилизации 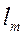 в кольцевой трубе при теплоотдаче на внутренней стенке используется формула
в кольцевой трубе при теплоотдаче на внутренней стенке используется формула
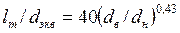 , (136) а при теплоотдаче на наружной стенке — формула
, (136) а при теплоотдаче на наружной стенке — формула
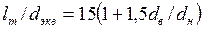 . (137)
. (137)
Если длина кольцевого канала меньше 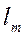 и
и 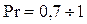 , то коэффициенты теплоотдачи
, то коэффициенты теплоотдачи 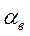 и
и 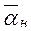 , определенные по (134) и (135), надо умножить на коэффициент
, определенные по (134) и (135), надо умножить на коэффициент 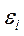 :
: 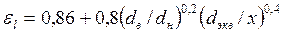 , если теплообмен на внутренней стенке;
, если теплообмен на внутренней стенке;  , если теплообмен на наружной стенке.
, если теплообмен на наружной стенке.
B. При движении потока в изогнутых трубах (змеевиках) со средним диаметром изгиба (витка) D и внутренним диаметром трубы 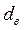 (рис. 9) теплоотдача происходит интенсивней вследствие появления центробежного эффекта. При расчете теплоотдачи определяется число
(рис. 9) теплоотдача происходит интенсивней вследствие появления центробежного эффекта. При расчете теплоотдачи определяется число 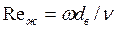 , которое сравнивается с двумя числами Рейнольдса:
, которое сравнивается с двумя числами Рейнольдса: 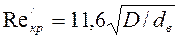 и
и 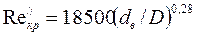 (при
(при 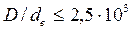 ).
).
Если 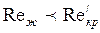 , то расчет теплоотдачи и сопротивления проводится по формулам для ламинарного движения в прямых трубах. Если
, то расчет теплоотдачи и сопротивления проводится по формулам для ламинарного движения в прямых трубах. Если 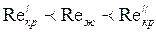 , то используется формула (127) для турбулентного течения в каналах. Если
, то используется формула (127) для турбулентного течения в каналах. Если 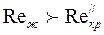 , то коэффициент теплоотдачи определяется по формуле (127) и умножался на
, то коэффициент теплоотдачи определяется по формуле (127) и умножался на 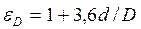 .
.
Г. Для продольно обтекаемых пучков труб, охлаждаемых газами и жидкостями, справедлива формула
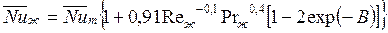 . (138) Здесь
. (138) Здесь 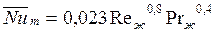 ;
; 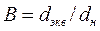 ; для расположения труб в пучке по треугольнику
; для расположения труб в пучке по треугольнику 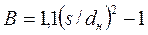 , для расположения труб по квадрату
, для расположения труб по квадрату 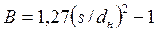 ; s — расстояние между осями труб (шаг);
; s — расстояние между осями труб (шаг); 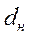 — наружный диаметр трубы;
— наружный диаметр трубы; 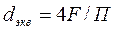 — определяющий геометрический размер.
— определяющий геометрический размер.
Формула справедлива при 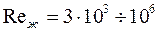 ;
; 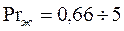 ;
; 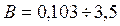 ;
;  .
.
В межтрубном пространстве кожухотрубных теплообменников без поперечных перегородок число Nu определяется по формуле (127) с определяющим размером
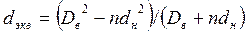 , (139) где
, (139) где 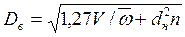 — внутренний диаметр кожуха;
— внутренний диаметр кожуха; 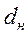 — наружный диаметр труб, м; n —число труб в пучке; V —объемный расход,
— наружный диаметр труб, м; n —число труб в пучке; V —объемный расход, 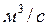 ;
; 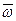 - средняя скорость потока в межтрубном пространстве, отнесена к живому сечению.
- средняя скорость потока в межтрубном пространстве, отнесена к живому сечению.
Если известен шаг s, то для пучков с коридорным (квадратным) расположением труб
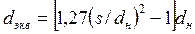 , (140) а для пучков с шахматным (треугольным) расположением
, (140) а для пучков с шахматным (треугольным) расположением
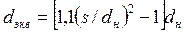 . (141)
. (141)
Для теплообменников с поперечными перегородками в межтрубном пространстве:
при коридорном расположении труб в пучке
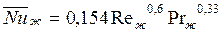 , (142)
, (142)
при шахматном расположении труб в пучке
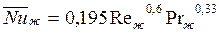 . (143)
. (143)
Определяющий размер 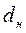 — наружный диаметр трубы, скорость вычисляется по среднему минимальному живому сечению:
— наружный диаметр трубы, скорость вычисляется по среднему минимальному живому сечению:
если перегородки сегментного типа,
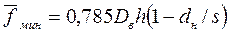 ; (144)
; (144)
если перегородки концентрического типа,
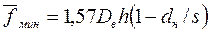 . (145)
. (145)
Здесь h — расстояние между соседними перегородками; шаг обычно принимается 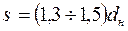 .
.
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 689; Нарушение авторских прав?; Мы поможем в написании вашей работы!