Замедленная коммутация

Прямолинейная коммутация

Прямолинейная коммутация происходит тогда, когда добавочный ток (r_доб) равен нулю.

Ток в коммутируемой секции равен

i=i_a 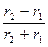, = , (1)

где S₁ - площадь соприкосновения пропорциональная времени оставшегося до конца коммутации - Т_к–t;

S₂ - площадь соприкосновения пропорциональная времени от начала коммутации - t.

Разделим уравнение (1) на r₂

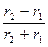I=i_a =i_a , = =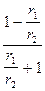

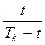
Заменим отношение на .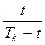

I=i_a , после преобразования получим закон изменения тока прямолинейной коммутации 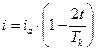, ток в коммутируемой секции. Графически это будет прямая линия.

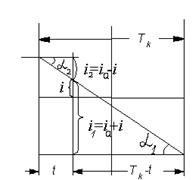На рис. 240 на момент времени t показаны токи i₁, i₂ и i. Эта коммутация самая хорошая, так как плотность тока под щеткой равномерно распределяется под обеими частями щетки.

Рис. 240.

tg a₂= 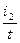º =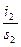

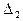
tg a₁=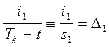

т.к. a₁=a₂, то tg a₁=tg a₂, а, следовательно, D₁=D₂ (D - плотность тока).

Так как период коммутации составляет тысячные доли секунды, то от скорости изменения тока в коммутируемой секции наводится ЭДС самоиндукции 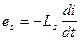. Кроме того, в пазу располагается другая активная сто­рона другой секции, которая коммутирует под другим полюсом. Ток этой секции наведет ЭДС взаимоиндукции в впервой коммутируемой секции 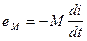. Обе эти ЭДС по природе одинаковы, поэтому объединим их в одну и назовем реактивной ЭДС - e_r.

Кроме того, в коммутируемой секции от внешнего поля наведется ЭДС - e_k. (e_k - ЭДС от внешнего поля или коммутирующая ЭДС). ЭДС e_r и e_k вызовут в секции добавочный ток 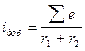, где r₁+r₂ - общее сопротивление под щеткой. Характер тока будет определяться характером суммарного значения ЭДС Se. Конечно, Se тоже меняется, но мы будем брать среднее значение и считать, что Se будет постоянной.

Посмотрим, как будет изменяться добавочный ток i_доб и сопротивление r₁+r₂ за период коммутации. Исходя из соотношения

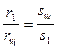, откуда 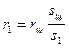. Аналогично, 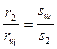, откуда 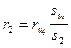. Так как s_щºT_k, а s₂ºt, s₁ºT_k-t, то r₁+r₂=r_щ .

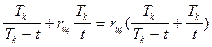При t=0, r₁+r₂=¥, i_доб =0

t=T_k, r₁+r₂=¥, i_доб=0

t=T_k/2, r₁+r₂=4r_щ, i_доб ¹0.

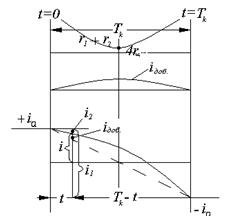На рис.61 представлено изменение суммы сопротивлений r₁+r₂ добавочному току. Видим, что при t=T_k/2 добавочный ток имеет наибольшее значение.

Рис. 241.

Результирующий ток в коммутируемой секции состоит из тока прямолинейной коммутации (пунктирная прямая) и добавочного тока. Так как при замедленной коммутации преобладает реактивная ЭДС, то процесс коммутации замедляется, т.е. ток в секции изменяет направление позже, чем при прямолинейной коммутации 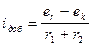. При замедленной коммутации e_r>e_k и добавочный ток i_доб увеличивает ток i₁ и уменьшает ток i₂, рис.242.

i₂

i₁

Рис. 242.

Поэтому равномерное распределение тока под щеткой будет нарушено. Плотность тока на сбегающей части щетки возрастает, и искрение будет наблюдаться на этой части щетки. Замедленная коммутация – это наихудший вид коммутации.

Дата добавления: 2014-11-20