Сведения из теории

Напряжение Ů_х и ток İ_x в точке, удаленной от конца линии на расстояние х для линии без потерь будут

Ů_х= Ů_ecosβx+i İ_e Z_csinβx, (1)

İ_x = İ_e cosβx+i sinβx, (2)

где i— мнимая единица;

х— декартова координата;

Z_c - волновое сопротивление.

Случай 1. R = Z_c

Для случая 1, когда сопротивление нагрузки R равно волновому сопротивлению Z_c, можно написать, что

Ů_е= İ_e Z_c

Тогда получим

Ů_x = Ů_e (cos βx + i sin βx) = Ů_ee^iβx (3)

İ_x = İ_e (cos βx + i sin βx) = İ_ее^βх (4)

Полагая, что напряжение в конце линии меняется по синусоидальному закону, выражения (3) и (4) можно записать так:

Ů_x = Ů_eme^i(ωt+βx)

İ_x = İ_eme^i(ωt+βx)

Отсюда мгновенные значения напряжения u_х и тока i_x можно записать в виде

u_x = U_вmsin(ωt+βx), (5)

i_x = I_вm sin(ωt+βx). (6)

Из этих выражений видно, что амплитудные значения напряжения и тока во всех точках линии одинаковы, а их фазы зависят от места положения точки на линии. Следовательно, в рассматриваемой линии имеет место бегу­щая волна. Коэффициент К_бв характеризует степень приближения режима в линии к режиму бегущей волны и поэтому называется коэффициентом бегущей волны. В процессе распространения волны напряжение и ток совпадают по фазе.

Из уравнений (5) и (6) видно также, что разность в фазах колебания между конечной точкой линии и любой, отстоящей от конца линии на расстоянии х, определяется расстоянием между этими точками и скоростью распространения волны вдоль линии. Это можно показать, вос­пользовавшись, например, уравнением (5):

u_х = U_вm sin ω(t + βx/ ω) = U_вmsin ω(t + x/ V_ф), (7)

где V_ф= ω/t – фазовая скорость распространения волны.

Таким образом, при нагрузке линии на активное сопротивление, равное ее волновому сопротивлению, в линии будут только бегущие волны, и энергия будет иметь чисто активный характер. Этот согласованный режим работы линии является наиболее выгодным режимом работы для передачи активной мощности. Поэтому в линиях передачи применяют специальные меры для получения в них режима бегущей волны.

Входное сопротивление в любой точке линии, нагруженной на активное сопротивление, равное ее волновому сопротивлению, как это видно из уравнений (3) и (4), будет равно волновому сопротивлению линии, т.е. Z_вх = Z_c

Случай 2. R>Z_c

Рассмотрим случай, когда линия без потерь замкнута на активное сопротивление R>Z_c

Получим для этого случая уравнения передачи. Имея в виду, что й_е =I_eR, для точки х можно написать:

Ů_x = İ_eZ_c (R/Z_ccos βx + i sin βx) (8)

İ_x = İ_e (cos βx + i R/Z_csin βx) (9)

Введем обозначение:

R/Z_c = K_бв (K_бв<1), (10)

где К_бв является коэффициентом бегущей волны.

Можно написать

Ů_x = İ_eZ_c (K_бв cos βx + i sin βx) (11)

İ_x = İ_e (cos βx + i K_бв sin βx) (12)

Полагая, что ток в нагрузке изменяется по синусоидальному закону, т. е. İ_е = I_вmе^itω, получим следующие выражения для мгновенных значений напряжения и тока:

u_x=I_вmZ_c K_бв sin(ωt+ βx) +I_вmZ_c (1-K_бв)sin βx sin(ωt+ π/2), (13)

i_x = I_вmK_бв sin(ωt+ βx) +I_вm(1-K_бв)cos βx sin ωt. (14)

Анализ этих выражений показывает, что первые слагаемые аналогичны выражениям (5) и (6) и описывают бегущую волну, а вторые слагаемые аналогичны, для стоячей волны в случае короткозамкнутой линии и отличаются только множителями (1–К_бв). Следовательно, в линии имеются как бегущие, так и стоячие волны; при этом, чем больше R отличается от Z_c (чем больше К_бв отличается от единицы), тем резче выявлены стоячие волны, и наоборот, чем ближе К_бв к единице, тем резче проявляют себя бегущие волны. При К_бв = 1, т. е. при R = Z_c, в линии будут только бегущие волны (режим согласованной нагрузки), при К_бв = 0 - только стоячие волны (режим короткого замыкания). При наложении двух распространяющихся в противоположных направлениях гармонических волн с одинаковыми амплитудами называется стоячей волной.

Распределение амплитуд напряжения и тока зависит от длины линии. Эта зависимость при значении К_бв =0,5 показана на рис. 1. Из рисунка следует, что при βx = 0, π, 2 π и т. д. амплитуды напряжения минимальны и равны U_min=I_emZ_cK_бв.

При βx = π /2, 3π /2 и т. д., наоборот, амплитуды напряжения максимальны и равны U_макс=I_еmZ_c.

Рис. 1. Изменение амплитудных значений

напряжения и тока в линии без потерь при нагрузке R > Z_c

Отношение этих амплитуд равно коэффициенту бегущей волны:

К_бв=U_мин/U_макс. (15)

Аналогичным путем можно получить, что

К_бв= I_макс/I_мин (16)

также равно коэффициенту бегущей волны. В этом случае минимумы амплитуд тока I (узлы тока) будут соответствовать максимумам амплитуд напряжения U (пучности напряжения) и наоборот.

Входное сопротивление линии Z_вx, нагруженной на активное сопротивление, меньшее волнового, можно получить, если взять отношение Ů_х к İ_x.

Производя необходимые преобразования, получим

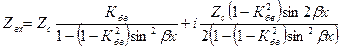(17)

Входное сопротивление имеет активную и реактивную составляющие входного сопротивления от длины линии показана на рис. 2, для которого К_бв =0,5.

Рис. 2. Изменение активной и реактивной составляющих входного сопротивления линии без потерь при нагрузке R > Z_c

Из рисунка 2 видно, что при х = 0, λ/2, λ и т. д. активная составляющая входного сопротивления имеет минимальное значение и равна сопротивлению нагрузки R_мин = R, а реактивная составляющая равна нулю. Следовательно,

Z_вх= R_вх= R_мин=Z_c K_бв= Z_c/ K_cв, (18)

При значениях х = λ/4, 3λ/4 и т. д. входное сопротивление также активно, имеет максимальное значение, но равно

Z_вх= R_вх= R_макс= Z_c²/R= Z_c²/R_мин =Z_c/K_бв= Z_cK_cв, (19)

где К_св — коэффициент стоячей волны.

Во всех других точках линии входное сопротивление имеет комплексный характер. При этом характер реактивности тот же, что и у короткозамкнутой линии.

Случай 3. R < Z_c

В случае R < Z_c аналогичным путем получим следующие выражения для мгновенных значений напряжения и тока:

u_х = U_em К_бв sin(ωt+ βx) + U_em (l - К_бв)cos βx sin ωt, (20)

i_x = (U_em/ Z_c) К_бв sin(ωt+ βx) + (U_em / Z_c)(l - К_бв)sin βx sin ωt (21)

Первые слагаемые этих уравнений описывают бегущую волну, а вторые - стоячую. Следовательно, в линии имеются как бегущие, так и стоячие волны. При К_бв = 1, т. е. при R<Z_c, в линии будут только бегущие волны, при К_бв= 0 – только стоячие волны. Следовательно, К_бв характеризует степень приближения режима в линии к режиму бегущей волны.

Зависимость амплитудных значений напряжения и тока от длины линии при К_бв = 0,5 показана на рис. 3. Из которого следует, что при βx = 0, π, 2 π и т. д.

Амплитуды напряжения максимальны и равны U_MAKC= U_em. При βx = π/2, 3π/2 и т. д., наоборот, амплитуды напряжения минимальны и равны

U_min=U_emK_бв= U_максK_бв (22)

Максимумы и минимумы амплитудных значений тока сдвинуты относительно соответствующих значений напряжения на π /2.

Сравнивая графики (рис. 2, 3), т. е. случаи R < Z_c и R > Z_c, нетрудно видеть, что они сдвинуты относительно друг друга на π/2 (х=λ/4) и что минимуму в одном случае соответствует максимум в другом, и наоборот.

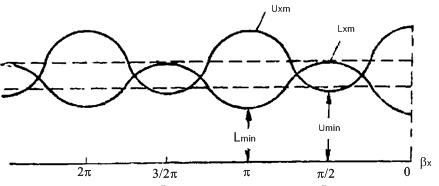
Рис. 3. Изменение амплитудных значений' напряжения и тока в линии без потерь при нагрузке R < Z_c

Важно отметить, что при R < Z_c первый минимум напряжения от конца линии будет отстоять на расстоянии х = λ/2, при R > Z_c — на расстоянии х = λ/4. Это важное свойство может быть использовано для определения ве­личины активного сопротивления, являющегося нагрузкой линии, по расстоянию первого узла напряжения от конца линии и коэффициенту бегущей или стоячей волны.

Зависимость R_вx и Х_вх от длины линии при КБВ – 0,5 показана на рис. 4.

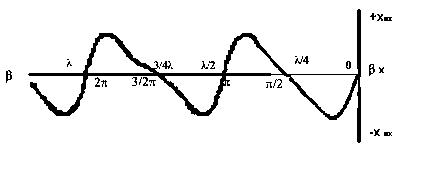
Рис. 4. Изменение активной и реактивной составляющих входного сопротивления линии без потерь при нагрузке R > Z_c

Из рис. 4 видно, что при fix = 0, λ, 2λ и т. д. реактивная составляющая равна нулю, а входное сопротивление чисто активно и равно максимальному значению R = R_makc– λ.

При fix = λ/2 (х = λ/4), 3λ/2 (х = 3λ/4) и т. д. входное сопротивление также активно, но равно минимальному значению.

Во всех других точках входное сопротивление имеет комплексный характер.

Дата добавления: 2014-11-20