
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Андай матрица квадрат матрица деп аталады? 3 страница
|
|
|
|
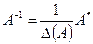
Қандай матрицаның кері матрицасы болады?
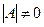 болса
болса
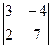 анықтауышын есепте
анықтауышын есепте
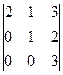 анықтауышын есепте
анықтауышын есепте
 матрицасының рангысының анықтамасы: осы матрицаның нөлге тең емес минорларының ең үлкен ретін айтады
матрицасының рангысының анықтамасы: осы матрицаның нөлге тең емес минорларының ең үлкен ретін айтады
Матрицаның
рангысы өзгермейді, егер:
кез келген екі жолын немесе екі бағанын ауыстырғаннан
Егер бір матрица екінші бір матрицадан элементар (жәй) түрлендіру арқылы алынса, онда ол матрицалар :
эквивалентті деп аталады.
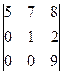 анықтауышын есепте
анықтауышын есепте
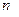 белгісізді
белгісізді 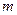 сызықты алгебралық теңдеулер жүйесі үйлесімді, егер:
сызықты алгебралық теңдеулер жүйесі үйлесімді, егер:
жүйенің негізгі матрицасының рангысы мен оның кеңейтілген матрицасының рангысына тең болса
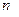 белгісізді
белгісізді 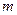 сызықты алгебралық теңдеулер жүйесінің бір ғана шешімі болады, егер:
сызықты алгебралық теңдеулер жүйесінің бір ғана шешімі болады, егер:
жүйенің негізгі матрицасының рангысы оның кеңейтілген матрицасының рангысына тең және ол белгісіздер саны 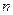 -ге тең, яғни
-ге тең, яғни 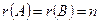
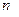 белгісізді
белгісізді 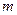 біртекті сызықты алгебралық теңдеулер жүйесі:
біртекті сызықты алгебралық теңдеулер жүйесі:
әруақытта үйлесімді
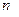 белгісізі бар
белгісізі бар 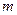 сызықты теңдеулер жүйесі
сызықты теңдеулер жүйесі 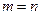 болғанда, мұнда
болғанда, мұнда 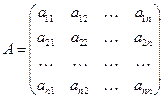
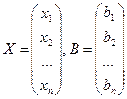 , матрицалық түрде былай беріледі.
, матрицалық түрде былай беріледі.
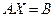
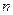 белгісізді
белгісізді 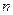 сызықты теңдеулер жүйесінің матрицалық әдіспен шешкендегі матрица - шешімі
сызықты теңдеулер жүйесінің матрицалық әдіспен шешкендегі матрица - шешімі 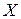 былай табылады:
былай табылады:
A) 
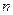 белгісізді
белгісізді 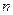 сызықты алгебралық теңдеулер жүйесінің
сызықты алгебралық теңдеулер жүйесінің 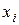 шешімі
шешімі  Крамер формуласы бойынша былай табылады:
Крамер формуласы бойынша былай табылады:
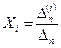
Бір текті 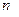 белгісізді
белгісізді 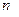 сызықты теңдеулер жүйесінің бір ғана шешімі бар:
сызықты теңдеулер жүйесінің бір ғана шешімі бар:
 , егер
, егер 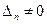
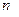 белгісізді
белгісізді 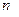 біртекті теңдеулер жүйесінің шексіз көп шешімі болады, егер:
біртекті теңдеулер жүйесінің шексіз көп шешімі болады, егер:

 анықтауышын есептеңіз:
анықтауышын есептеңіз:
-2
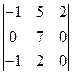 анықтауышын есептеңіз:
анықтауышын есептеңіз:
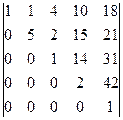 анықтауышын есептеңіз:
анықтауышын есептеңіз:
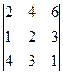 анықтауышын есептеңіз:
анықтауышын есептеңіз:
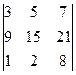 анықтауышын есептеңіз:
анықтауышын есептеңіз:
 анықтауышын есептеңіз:
анықтауышын есептеңіз:
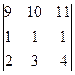 анықтауышының
анықтауышының 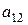 элементінің минорын есептеңіз:
элементінің минорын есептеңіз:
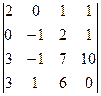 анықтауышының
анықтауышының 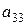 элементінің минорын есептеңіз :
элементінің минорын есептеңіз :
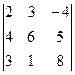 анықтауышының
анықтауышының  элементінің минорын есептеңіз :
элементінің минорын есептеңіз :
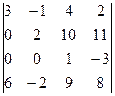 анықтауышының
анықтауышының 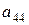 элементінің минорын есептеңіз :
элементінің минорын есептеңіз :
 анықтауышының
анықтауышының  элементінің
элементінің 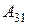 алгебралық толықтауышын есептеңіз:
алгебралық толықтауышын есептеңіз:
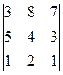 анықтауышының
анықтауышының 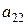 элементінің
элементінің 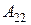 алгебралық толықтауышын
алгебралық толықтауышын
есептеңіз:
-4
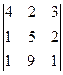 анықтауышының
анықтауышының 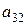 элементінің
элементінің 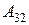 алгебралық толықтауышын
алгебралық толықтауышын
есептеңіз:
-5
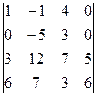 анықтауышының
анықтауышының 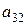 элементінің
элементінің 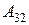 алгебралық толықтауышын есептеңіз:
алгебралық толықтауышын есептеңіз:
-18
Теңдеуді шешіңіз 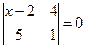
Теңдеуді шешіңіз 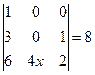
- 2
Теңдеуді шешіңіз 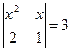
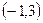
Теңдеуді шешіңіз 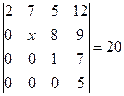
Теңдеуді шешіңіз 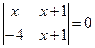
Теңдеуді шешіңіз 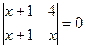

 матрицасын есептеңіз, мұндағы
матрицасын есептеңіз, мұндағы 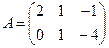 ,
, 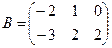
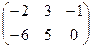
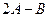 матрицасын табыңыз, мұндағы
матрицасын табыңыз, мұндағы 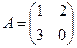 ,
, 
табу мүмкін емес
 , және
, және 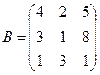 матрицаларының қосындысын табыңыз:
матрицаларының қосындысын табыңыз:
қосу мүмкін емес
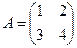 және
және 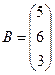 матрицаларының
матрицаларының 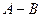 айырымын табыңыз:
айырымын табыңыз:
азайту мүмкін емес
 матрицасын 2-ге көбейтіңіз:
матрицасын 2-ге көбейтіңіз:
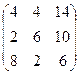
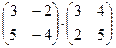 көбейтіндісін есептеңіз:
көбейтіндісін есептеңіз:
 көбейтіндісін есептеңіз:
көбейтіндісін есептеңіз:
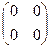
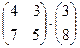 көбейтіндісін есептеңіз:
көбейтіндісін есептеңіз:

 көбейтіндісін есептеңіз:
көбейтіндісін есептеңіз:
көбейту мүмкін емес,
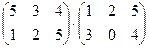 көбейтіндісін есептеңіз:
көбейтіндісін есептеңіз:
көбейту мүмкін емес
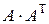 көбейтіндісін есептеңіз, мұндағы
көбейтіндісін есептеңіз, мұндағы 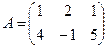 ,
, 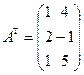 :
:

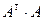 көбейтіндіс ін есептеңіз, мұндағы
көбейтіндіс ін есептеңіз, мұндағы 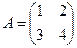 ,
, 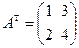 :
:
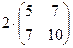
Есептеңіз 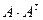

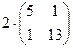
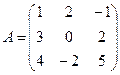 матрицасын бірлік матрицаға көбейтіңіз:
матрицасын бірлік матрицаға көбейтіңіз:
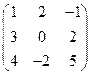
 және
және 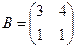 берілгендері бойынша
берілгендері бойынша  көбейтіндісін табыңыз:
көбейтіндісін табыңыз:
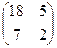
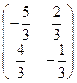
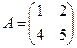 матрицасына кері матрицаны табыңыз:
матрицасына кері матрицаны табыңыз:
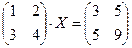 -матрицалық теңдеуді шешіңіз:
-матрицалық теңдеуді шешіңіз:
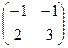
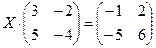 теңдеуін шешіңіз:
теңдеуін шешіңіз:
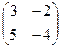
 теңдеуін шешіңіз:
теңдеуін шешіңіз:

 матрицасына кері матрицаны табыңыз:
матрицасына кері матрицаны табыңыз:
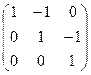
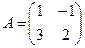 матрицасына кері матрицаны табыңыз:
матрицасына кері матрицаны табыңыз:
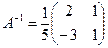
 матрицасына кері матрицаны табыңыз:
матрицасына кері матрицаны табыңыз:
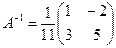
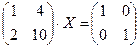 - теңдеуін шешіңіз:
- теңдеуін шешіңіз:

 - теңдеуін шешіңіз:
- теңдеуін шешіңіз:

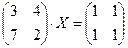 теңдеуін шешіңіз:
теңдеуін шешіңіз: 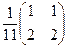
теңдеулер жүйесін шешіңіз:
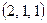
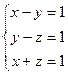 теңдеулер жүйесін шешіңіз:
теңдеулер жүйесін шешіңіз:
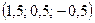
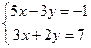 теңдеулер жүйесін шешіңіз:
теңдеулер жүйесін шешіңіз:

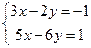 теңдеулер жүйесін шешіңіз:
теңдеулер жүйесін шешіңіз:
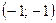
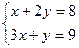 теңдеулер жүйесін шешіңіз:
теңдеулер жүйесін шешіңіз:
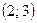
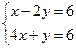 теңдеулер жүйесін шешіңіз:
теңдеулер жүйесін шешіңіз:
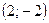
 теңдеулер жүйесін шешіңіз:
теңдеулер жүйесін шешіңіз:
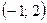
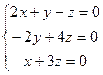 теңдеулер жүйесін шешіңіз:
теңдеулер жүйесін шешіңіз:
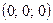
 теңдеулер жүйесін шешіңіз:
теңдеулер жүйесін шешіңіз:
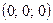
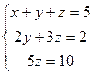 теңдеулер жүйесін шешіңіз:
теңдеулер жүйесін шешіңіз:
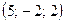
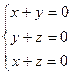 теңдеулер жүйесін шешіңіз:
теңдеулер жүйесін шешіңіз:
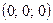
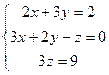 теңдеулер жүйесін шешіңіз:
теңдеулер жүйесін шешіңіз:
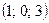
 т
т  еңдеулер жүйесін шешіңіз:
еңдеулер жүйесін шешіңіз:
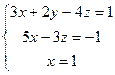 теңдеулер жүйесін шешіңіз:
теңдеулер жүйесін шешіңіз:
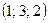
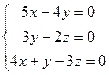 теңдеулер жүйесін шешіңіз:
теңдеулер жүйесін шешіңіз:
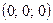
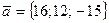 векторының модулін табыңыз
векторының модулін табыңыз
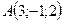 және
және 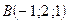 нүктелері берілген.
нүктелері берілген. 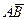 векторының координаталарын табыңыз
векторының координаталарын табыңыз
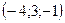
 және
және 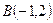 нүктелері берілген.
нүктелері берілген. 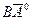 бірлік векторының координаталарын көрсетіңіз
бірлік векторының координаталарын көрсетіңіз
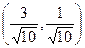
Бір түзуде немесе параллель түзулердің бойында жатқан векторлар қалай аталады?
Коллинеарлы
Бір жазықтықта жатқан векторлар қалай аталады?
Компланарлы
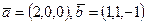 векторлары берілген.
векторлары берілген. 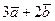 векторының ұзындығын есептеңіз
векторының ұзындығын есептеңіз
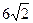
 және
және 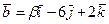 векторлары
векторлары 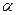 мен
мен 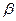 -ның қандай мәндерінде коллинеар болады?
-ның қандай мәндерінде коллинеар болады?
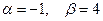
 және
және 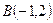 нүктелері берілген.
нүктелері берілген. 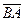 векторының координаталарын табыңыз
векторының координаталарын табыңыз
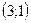
Егер 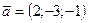 векторының ұшы
векторының ұшы 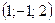 нүктесінде болса, онда осы вектордың басының координаталары неге тең?
нүктесінде болса, онда осы вектордың басының координаталары неге тең?
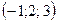
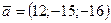 векторының бағыттаушы косинустарын табыңыз
векторының бағыттаушы косинустарын табыңыз
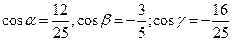
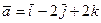 векторының базистік векторларымен жасайтын бұрыштарының косинустарын табыңдар
векторының базистік векторларымен жасайтын бұрыштарының косинустарын табыңдар
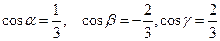
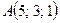 және
және 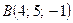 нүктелері берілген.
нүктелері берілген. 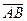 векторының ұзындығын табыңыз
векторының ұзындығын табыңыз
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 887; Нарушение авторских прав?; Мы поможем в написании вашей работы!