Поиск путей в графе

Элементы теории графов.

Решение.

Так как данная матрица содержит две строки и четыре столбца, то она может быть (4,2) кодом. Для проверки умножим каждую строку 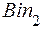на данную матрицу слева. Имеем:

Таким образом,

Поскольку все полученные строки различны, то отображение инъективно, а следовательно, является кодом.

Так как строки (1) и (3) множества отличаются ровно на два бита (), то код не является кодом Хемминга.

Путь в графе называется простым, если ни одна вершина в нем не повторяется (для контура допускается ).

Вершины х и у графа, соединенные дугой, называют смежными.

Говорят, что вершины инцидентны ребру (дуге).

Степень вершины графа – это число ребер, ей инцидентных.

Зафиксируем в графе 2 вершины А и В. Исторически возникли 3 задачи о поиске путей в графе.

Задача 1. Найти любой (или простой, или гамильтонов, или эйлеров) путь (цепь) из А в В.

1. Дан граф (рис.4).

Найти все простые пути из А в В. Показать один из них на рисунке.

Решение. Обозначим все вершины графа буквами. Используя определение простого пути, получим простые пути в данном графе. Перечислим их (рис.5).

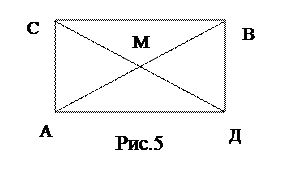
АСВ

АСМВ

АСМДВ

АДВ

АДМВ

АДМСВ

АМВ

АМСВ

АМДВ

Покажем один из этих путей на рис. 6.

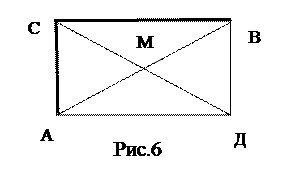
Задача 2. Найти кратчайший путь из А в В в смысле количества ребёр (дуг).

2. Дан граф (рис.7).

а) определить степени вершин А и В.

б) найти кратчайший путь из точки А в точку В (в смысле наименьшего количества ребер).

Дата добавления: 2014-11-20