
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. Пронумеруем вершины графа, выпишем матрицу смежности и ее верхний треугольник (рис
|
|
|
|
Решение.
Пронумеруем вершины графа, выпишем матрицу смежности и ее верхний треугольник (рис. 17).








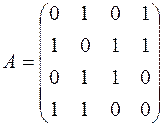 , верхний треугольник, записанный в виде строки, имеет вид 01010111002 = 34810.
, верхний треугольник, записанный в виде строки, имеет вид 01010111002 = 34810.
Легко увидеть, что данная нумерация вершин не является канонической. Действительно, сменим нумерацию вершин (рис. 18).







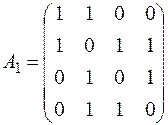 , верхний треугольник, записанный в виде строки, имеет вид 11000110102 = 79410.
, верхний треугольник, записанный в виде строки, имеет вид 11000110102 = 79410.
Можно убедиться, что при всех других способах нумерации вершин получаются числа, меньшие 794. следовательно, последняя нумерация вершин является канонической, а кодом Харари данного графа является число 794.
3. Восстановить и нарисовать граф по числу 501 как по коду Харари. Проверить, действительно ли нумерация вершин каноническая (то есть, является ли это число кодом Харари).
Переведем число 501в двоичную форму, для чего будем последовательно делить его на 2, справа от черты записывая остатки от деления, а слева на следующей строке частные.
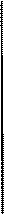 501 1
501 1
250 0
125 1
062 0
031 1
015 1
007 1
003 1
Затем выписываем число, начиная с последнего частного, и далее все остатки снизу вверх: 01111101012. Код Харари должен быть треугольным числом, т.е. иметь длину 1, 3, 6, 10, 15, 21 и т.д., если длина, как в нашем случае, не совпадает ни с одним из этих чисел, то добавляем слева необходимое количество нулей (в данном примере добавлен один ноль слева). Разбиваем число на разряды: 0111-110-10-1, вписываем эти числа в верхний треугольник матрицы, затем восстанавливаем всю матрицу, записывая ее строки по столбцам:

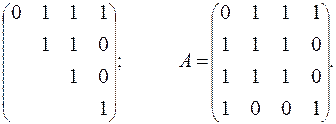
Восстанавливаем по этой матрице граф с четырьмя вершинами (рис. 19):
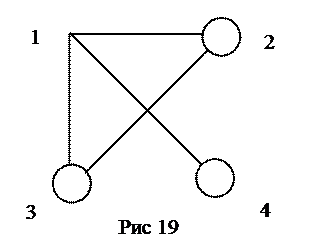

Заметим, что данная нумерация вершин не является канонической. Перенумеруем вершины (рис. 20):
 |
Для получившегося графа матрица смежности






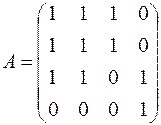 , верхний треугольник, записанный в виде строки, имеет вид 11101100112 = 94710.
, верхний треугольник, записанный в виде строки, имеет вид 11101100112 = 94710.
947 > 501, значит, число 501 не является кодом Харари графа.
3. Найти префиксный код бинарного ордерева (рис.21).
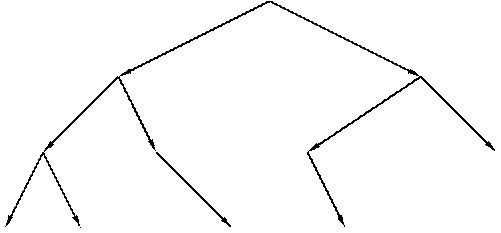
Рис. 21
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 2019; Нарушение авторских прав?; Мы поможем в написании вашей работы!