Задачи о раскраске графа

Решение.

При выполнении данного задания необходимо соблюдать порядок обхода для любой вершины ордерева, в которой мы находимся в тот или иной момент времени.

1. Прямой обход (КЛП – обойти корень, левое поддерево, затем правое поддерево): .

2. Обратный обход (ЛКП – обойти левое поддерево, корень, затем правое поддерево): .

3. Концевой обход (ЛПК – обойти левое поддерево, правое поддерево, затем корень): .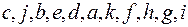

О п р е д е л е н и е. Граф допускает 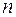-цветную раскраску вершин, если его вершины можно раскрасить 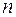красками так, чтобы никакие две смежные вершины не имели бы одинаковый цвет.

Минимальное число 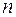, при котором граф 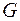допускает 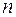-раскраску вершин, называется хроматическим числом графа (обозначается ).

П о с т а н о в к а з а д а ч и. Дан связный граф. Требуется найти значение хроматического числа и соответствующую раскраску вершин.

А л г о р и т м р е ш е н и я.

1. Вычислить степени всех вершин, положить .

2. Расположить вершины по убыванию их степеней и первую из неокрашенных вершин окрасить в цвет .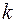

3. Просмотреть вершины в порядке убывания степеней и окрасить в цвет № 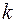все вершины, которые несмежны с вершинами, уже окрашенными в цвет № .

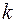4. Если все вершины уже окрашены, то 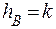. Если нет, то 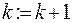и переходим к шагу 2.

О п р е д е л е н и е. Правильная раскраска рёбер графа – это раскраска рёбер графа некоторым количеством цветов так, чтобы никакие два инцидентных ребра графа не были окрашены в одинаковые цвета.

Минимальное число цветов необходимое для правильной раскраски рёбер графа называется хроматическим индексом графа (обозначается ).

Дата добавления: 2014-11-20