Расчетно-графическая работа

ЗАДАНИЕ 1

Решить систему линейных алгебраических уравнений тремя способами: 1) методом Гаусса; 2) по формулам Крамера; 3) матричным способом.

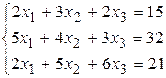
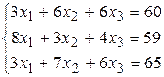
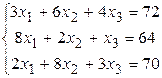
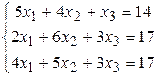
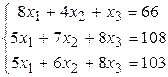
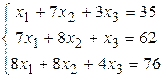
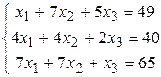
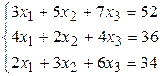
ЗАДАНИЕ 2

Дано: угол между векторами и равен Значения коэффициентов l, m, n, k, f и модули векторов и приведены в табл.

Определите:1)длины диагоналей параллелограмма, построенного на векторах 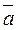и ;2)угол между диагоналями;3)площадь параллелограмма.

Вариант	p	q	l	m	n	k	f
Вариант	p	q	l	m	n	k	f

ЗАДАНИЕ 3

Даны точки А и В. Из точки А выходит луч, направленный по вектору . Найти координаты вектора , который пересекает луч, перпендикулярен ему и равен .

Вари-ант	А	В		Вари-ант	А	В
	(-3;4;2)	(1;12;3)		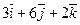	(5;1;-3)	(9;8;1)
	(1;2;-4)	(4;6;8)		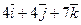	(1;2;-1)	(-9;-9;1)
	(-6;5;3)	(-5;7;5)			(5;-3;2)	(8;3;0)
	(2;2;-1)	(8;-4;6)			(-4;9;-7)	(4;-7;4)
	(4;-1;2)	(10;5;9)			(2;2;5)	(1;4;3)
	(-1;-9;2)	(0;9;8)			(8;3;3)	(4;-5;4)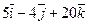
	(-7;-6;3)	(8;4;9)			(-6;7;9)	(6;-2;1)
	(-2;-1;5)	(4;-3;8)			(7;-5;-3)	(-8;1;7)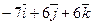
	(3;-1;4)	(5;1;5)			(-8;2;5)	(6;4;0)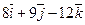
	(1;-1;3)	(5;0;11)			(1;-7;-9)	(2;5;3)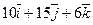
	(3;-1;0)	(9;-3;9)			(3;3;1)	(9;-3;8)
	(-4;1;1)	(3;5;5)			(2;9;6)	(8;-9;5)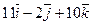
	(-5;0;2)	(1;-6;9)			(5;-1;2)	(6;-5;-6)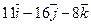
	(-7;5;5)	(5;1;2)			(-7;2;1)	(-9;5;7)
	(1;8;3)	(9;-8;-8)		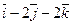	(3;2;5)	(-1;6;-2)

ЗАДАНИЕ 4

Даны координаты вершин пирамиды А₁, А₂, А₃, А_4. Построить пирамиду.

Найти: 1) длину ребра А₁А₂;

2) угол между ребрами А₁А₂ и А₁А₄;

3) угол между ребром А₁А₄ и гранью А₁А₂А₃;

4) площадь грани А₁А₂А₃;

5) объем пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости грани А₁А₂А₃;

8) уравнение высоты, опущенной из вершины А₄ на грань

А₁А₂А₃.

Вариант	А1	А2	А3	А4
	(2; 3; 2)	(10; 7; 3)	(6; 6; 3)	(8; 9; 5)
	(3; 5; 2)	(1; 7; 5)	(5; 6; 8)	(1; 6; 4)
	(6; 1; 4)	(3;-3; 8)	(5;-5; 8)	(8; 3; 3)
	(2; 5; 4)	(5; 3; 6)	(8; 3; 5)	(8; 2; 10)
	(3; 4; 3)	(7;-4; 4)	(6; 0; 4)	(9; 10; 6)
	(1; 2; 3)	(3; 4; 6)	(-3; 1; 6)	(3; 3; 5)
	(3; 5; 1)	(0; 1; 5)	(1; 0; 5)	(7; 9; -1)
	(5;-2; 4)	(7; 1; 6)	(7; 4; 5)	(8; 4; 10)
	(1; 2; 1)	(9;-2; 2)	(-3; 5; 0)	(7; 8;-2)
	(4; 1; 3)	(2; 3; 6)	(5;-3; 6)	(3; 3; 5)
	(3;-1; 2)	(7; 2; 6)	(9; 0; 6)	(5; 1; 3)
	(3; 5; 4)	(1; 8; 6)	(-1; 2; 6)	(9;-1; 1)
	(1; 1; 2)	(-3;9; 3)	(-2; 5; 3)	(7; 7; -1)
	(1; 4; 3)	(-1; 6; 6)	(6; -4; 0)	(2; 2; 1)
	(2; 4; 1)	(6; 7; 5)	(7; 6; 5)	(6; 8; 3)
	(1; 2; 2)	(3; 5; 4)	(5;-1; 4)	(7; 8; 5)
	(2;-2; 1)	(10; 2; 2)	(6; 1; 2)	(8; 4; 4)
	(3; 4;-1)	(1; 6; 2)	(5; 5; 5)	(1; 5; 1)
	(2; 5; 3)	(-1; 1; 7)	(1; -1; 7)	(4; 7; 2)
	(1; 4; 2)	(4; 2; 4)	(7; 2; 3)	(7; 1; 8)
	(3; 1; 4)	(7; -7; 5;)	(6; -3; 5)	(9; 7; 7)
	(2; 4; 3)	(4; 6; 6)	(-2; 3; 6)	(4; 5; 5)
	(5;-2;-1)	(2; -6; 3)	(3; -7; 3)	(9; 2; -3)
	(5; 2; 1)	(7; 5; 3)	(7; 8; 2)	(8; 8; 7)
	(2;-1; 7)	(10;-5; 8)	(-2; 2; 6)	(8; 5; 4)
	(4; 7; 8)	(2; 9; 11)	(5; 3; 11)	(3; 9; 10)
	(2; 1; 3)	(6; 4; 7)	(8; 2; 7)	(4; 3; 4)
	(1; 5; 2)	(-1; 8; 4)	(-3; 2; 4)	(7; -1;-1)
	(6; 1; 4)	(2; 9; 5)	(3; 5; 5)	(12; 7; 1)
	(6; 5; 1)	(4; 7; 4)	(11; -3; -2)	(7; 3;-1)

ЗАДАНИЕ 5

1. Написать уравнение эллипса, проходящего через точку пересечения гиперболы х² – у² = 2 с прямой х + у – 2 = 0, если известно, что фокусы эллипса совпадают с фокусами гиперболы.

2. Составить уравнение гиперболы, имеющей общие фокусы с эллипсом 24х² + 49у² = 1176 при условии, что ее эксцентриситет e = 1,25.

3. Написать уравнение окружности такой, чтобы ее диаметром оказался отрезок прямой х + у – 4 = 0, заключенный между осями координат.

4. Большая ось эллипса втрое больше его малой оси. Составить каноническое уравнение этого эллипса, если он проходит через точку М(3;Ö3).

5. Дана гипербола х² – у² = 8. Составить уравнение эллипса, проходящего через точку М(4;6) и имеющего фокусы, которые совпадают с фокусами данной гиперболы.

6. Найти точки пересечения параболы у² = 8х с эллипсом, у которого правый фокус совпадает с фокусом этой параболы, большая полуось равна 4 и фокусы лежат на оси Ох.

7. Фокусы гиперболы лежат в точках F₁(Ö7;0) и F₂(-Ö7;0). Гипербола проходит через точку А(2;0). Найти уравнения ее асимптот.

8. Найти параметр р параболы у² = 2рх, если известно, что эта парабола проходит через точки пересечения прямой у = х с окружностью х² + у² – 6х = 0.

9. Найти точки пересечения параболы у² = х с прямой, проходящей через фокус этой параболы параллельно ее директрисе.

10. Через правый фокус гиперболы 4х² – 5у² = 20 проведены прямые, параллельные ее асимптотам. Определить точки пересечения этих прямых с гиперболой.

11. Написать уравнение окружности, чтобы ее центр совпадал с фокусом параболы у² = 8х и чтобы окружность прошла через начало координат.

12. Оси гиперболы совпадают с осями координат. Гипербола проходит через точки пересечения параболы х² = 2у с прямой х – 2у + 6 = 0. Составить уравнение этой гиперболы.

13. Эллипс проходит через точку пересечения прямой 3х + 2у = 7 с параболой у² = 4х (взять точку с меньшей абсциссой). Оси эллипса совпадают с осями координат. Составить уравнение этого эллипса, если его эксцентриситет равен 0,6.

14. Эксцентриситет гиперболы в 2 раза больше углового коэффициента ее асимптоты. Гипербола проходит через точку М(3;-1), ее действительная ось лежит на оси Ох, а центр в начале координат. Найти точки пересечения этой гиперболы с окружностью х² + у² = 10.

15. Написать уравнение параболы, вершина которой находится в начале координат, а осью симметрии является ось Ох, если известно, что расстояние от ее фокуса до центра окружности х² + у² – 10х – 8у+ + 25 = 0 равно 5.

16. Составить каноническое уравнение эллипса, правая вершина которого совпадает с правым фокусом гиперболы 8х² – у² = 8. Эллипс проходит через точки пересечения параболы у² = 12х с данной гиперболой.

17. Вычислить расстояние от фокуса гиперболы 4х² – 5у² = 20 до ее асимптот. Найти эксцентриситет этой гиперболы.

18. Найти точки пересечения параболы у² = х с окружностью, которая проходит через начало координат, имеет центр на оси Ох и радиус, равный 5.

19. Составить уравнение эллипса, если его фокусы совпадают с фокусами гиперболы 4х² – 5у² = 20, а эксцентриситет эллипса равен 0,6.

20. Окружность имеет центр в левой вершине гиперболы х² – 4у² = =16 и радиус, равный вещественной полуоси этой гиперболы. Найти точки пересечения этой окружности с асимптотами данной гиперболы.

21. Составить уравнение гиперболы, имеющей эксцентриситет e= 1,5, если известно, что ее фокусы совпадают с фокусами эллипса 2х² + +5у² = 30.

22. Составить уравнение окружности, диаметром которой служит отрезок прямой х + у – 4 = 0, вырезанный параболой у² = 2х.

23. Найти расстояние от фокуса параболы 8у = х² до прямой 3х + +4у + 2 = 0.

24. Написать уравнение окружности, проходящей через точки А(3;0) и В(-1;2), если известно, что ее центр лежит на прямой х – у + 2 = 0.

25. Вычислить расстояние от центра окружности х² + у² = 10х до асимптот гиперболы х² – 4у² = 20.

26. Составить каноническое уравнение эллипса, сумма полуосей которого равна 8 и расстояние между фокусами равно 8.

27. В эллипс 24х² + 49у² = 1176 вписан прямоугольник, две противоположные стороны которого проходят через фокусы. Вычислить площадь этого прямоугольника.

28. Составить уравнение окружности, проходящей через точки А(5;0) и В((1;4), если центр ее лежит на прямой х + у = 3.

29. Написать каноническое уравнение эллипса, у которого эксцентриситет равен 0,8, а большая полуось больше малой полуоси на 2 единицы.

30. Найти каноническое уравнение гиперболы, проходящей через точку М(Ö40;2) и имеющей асимптоты 3у = ±х.

ЗАДАЧА 6

Изобразить на чертеже области, определяемые системой неравенств.

Вариант 1

.

Вариант 2

.

Вариант 3

.

Вариант 4

.

Вариант 5

.

Вариант 6

.

Вариант 7

.

Вариант 8

.

Вариант 9

.

Вариант 10

.

Вариант 11

.

Вариант 12

.

Вариант 13

.

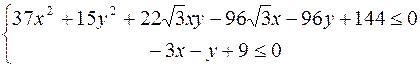Вариант 14

.

Вариант 15

.

Вариант 16

.

Вариант 17

.

Вариант 18

.

Вариант 19

.

Вариант 20

.

Вариант 21

.

Вариант 22

.

Вариант 23

.

Вариант 24

.

Вариант 25

.

Вариант 26

.

Вариант 27

.

Вариант 28

.

Вариант 29

.

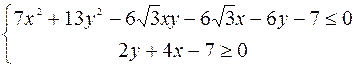Вариант 30

.

ЗАДАНИЕ 7

Привести к каноническому виду уравнение поверхности второго порядка с помощью теории квадратичных форм. Сделать чертеж поверхности в канонической системе координат.

1. х²+4ху+у²+z²=0.

2. х²+4ху+у²+2z²-6=0.

3. х²+4ху+у²-2z²=0.

4. х²+4ху+у²-3z²+12=0.

5. 2х²-6ху+2у²+z²=0.

6. 2х²-6ху+2у²+2z²-25=0.

7. 3х²+4ху+3у²+2z²-50=0.

8. 3х²+4ху+3у²-2z²=0.

9. 3х²+4ху+3у²-z²-100=0.

10. 2хz-3y²=0.

11. х²+4ху+у²-4z²-12=0.

12. 2ху-3z²=0.

13. х²+4хz+5у²+z²=0.

14. 3x²-2yz=0.

15. х²+6хz+5у²+z²-15=0.

16. 2х²+4у²+2z²+2xz-12=0.

17. 2х²-3у²+2z²+2xz=0.

18. 2х²-3у²+2z²-2xz-12=0.

19. 2х²-3у²+2z²-6xz+36=0.

20. 2х²+2у²+2z²+2yz-1=0.

21. 2х²-2у²-2yz -2z²+1=0.

22. 2х²-2у²-6yz- 2z²-1=0.

23. х²-у²-yz-z²=0.

24. х²-3у²-2yz-3z²-1=0.

25. х²+3у²+2yz+3z²+1=0.

26. 3х²-3у²-2yz-3z²=0.

27. 2х²-3у²-2yz-3z²-1=0.

28. х²+2у²+6yz+2z²+10=0.

29. 3х²+2у²-6yz+2z²-10=0.

30. х²+у²-6yz+z²=0.

Дата добавления: 2014-11-20