Вопросы к экзамену по дисциплине

ПРИМЕР ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ

ПРИМЕР ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ

ПО ТЕМЕ «ВЕКТОРНАЯ АЛГЕБРА»

1. Даны точки А (4;4;9), B (1;9;-1), C (3;7;4) и D (4;7;6).

Вычислить:

а) объем тетраэдра ABCD;

б) площадь грани ABC;

в) угол между вектором 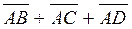и высотой тетраэдра, опущенной из вершины А;

г) проекцию вектора на вектор ;

д) координаты вектора в базисе 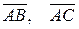и .

2. Найти площадь и угол между диагоналями параллелограмма, построенного на векторах 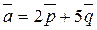и , если и угол между векторами и равен 45^о.

ПО ТЕМЕ «АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»

1. Даны точки А (-2;-5), B (4;4) и C (8;-3). Пусть C ₁ – точка, симметричная точке C относительно прямой АВ. Написать уравнение прямой, проходящей через точку C ₁ и составляющей угол 30^о с осью Ох.

2. Составить уравнение геометрического места точек, сумма квадратов расстояний которых до точек А (-4;0) и В(4;0) равна 40.

3. Написать уравнение прямой, проходящей через правый фокус эллипса 9х² +25у²=225 и точку А(-1;-3).

4. Написать уравнение плоскости, проходящей через прямую параллельно прямой .

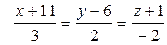«АЛГЕБРА И ГЕОМЕТРИЯ»

1. Определители. Вычисление определителей порядка n ≤ 3. Свойства определителей.

2. Миноры. Алгебраические дополнения. Теорема Лапласа.

3. Матрицы. Основные операции над матрицами.

4. Обратная матрица. Алгоритм вычисления.

5. Ранг матрицы. Вычисление ранга матрицы с помощью элементарных преобразований.

6. Линейная зависимость и независимость строк (столбцов) матрицы. Теорема Кронекера–Капелли.

7. Системы линейных алгебраических уравнений. Формулы Крамера.

8. Системы линейных алгебраических уравнений. Решение с помощью обратной матрицы.

9. Системы линейных алгебраических уравнений. Метод Гаусса.

10. Векторы и простейшие действия над ними.

11. Базис в пространстве, на плоскости и на прямой. Компонента (составляющая) вектора по (вдоль) оси. Проекция вектора на ось. Направляющие косинусы вектора. Теоремы о векторах.

12. Системы координат: декартова, декартова прямоугольная, полярная, цилиндрическая, сферическая.

13. Скалярное произведение векторов. Угол между векторами. Условие коллинеарности векторов.

14. Ориентация тройки векторов. Векторное произведение векторов. Свойства векторного произведения. Выражение векторного произведения через координаты сомножителей.

15. Смешанное произведение векторов. Свойства смешанного произведения. Выражение смешанного произведения через координаты сомножителей.

16. n – мерный вектор и векторное пространство.

17. Линейные преобразования. Действия над линейными преобразованиями.

18. Собственные значения и собственные векторы линейного преобразования.

19. Евклидово пространство. Ортогональные преобразования.

20. Квадратичные формы. Приведение к каноническому виду.

21. Алгебраическая линия на плоскости. Понятие об инвариантах. Параметрические уравнения линий.

22. Прямая на плоскости: параметрические уравнения, каноническое уравнение, уравнение с угловым коэффициентом.

23. Прямая на плоскости: общее уравнение, уравнение в отрезках, векторное уравнение.

24. Прямая на плоскости: уравнение прямой, проходящей через две точки; уравнение прямой, проходящей через данную точку в данном направлении; угол между прямыми; условия параллельности и перпендикулярности прямых.

25. Окружность и эллипс.

26. Гипербола.

27. Парабола.

28. Общее уравнение линии второго порядка и его инварианты. Классификация линий второго порядка и определение параметров канонических уравнений.

29. Общее уравнение линии второго порядка. Определение положения канонической системы координат.

30. Плоскость: общее уравнение, параметрические уравнения, векторное уравнение, уравнение в отрезках.

31. Уравнение плоскости, проходящей через три точки. Расстояние от точки до плоскости. Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей.

32. Прямая в пространстве: параметрические уравнения, каноническое уравнение, общее уравнение.

33. Угол между двумя прямыми. Расстояние от точки до прямой. Кратчайшее расстояние между двумя прямыми.

34. Параметрические уравнения поверхностей. Конусы. Уравнения, не содержащие одной из координат.

35. Поверхности вращения. Алгебраическая поверхность.

36. Поверхности второго порядка. Эллипсоиды. Гиперболоиды.

37. Поверхности второго порядка. Эллиптический параболоид. Гиперболический параболоид.

38. Приведение к каноническому виду уравнения поверхности второго порядка с помощью теории квадратических форм.

Дата добавления: 2014-11-20