Запись логической функции с помощью базовых операций

Каждому набору переменных соответствует один терм и только один вида такой, что он будет равен 1 для рассматриваемой комбинации и 0 для всех остальных комбинаций.

Например, комбинация переменных 011 дает терм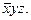

Если записать сумму всех термов, соответствующих комбинациям, на которых функция равна 1, то получим функцию, удовлетворяющую таблице соответствия (таблице истинности), т. е. определим эту функцию.

Данный метод записи функции в форме суммы произведений называется “ канонической суммой ”.

Можно было бы найти такой же терм в форме 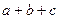, равный 0 для одной единственной комбинации и 1 для всех остальных комбинаций. Тогда функция будет записана в форме произведения подобных термов, и будет называться “ каноническим произведением ”.

Пример. Проиллюстрируем эти методы записи логической функции на примере получения логической формулы функции, представленной нижеследующей таблицей:

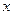
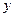
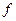
В соответствии с первым методом рассматриваем только строки таблицы, в которых функция равна 1. Это будут вторая и третья строки функции 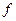. Логические формулы, соответствующие каждой из этих единиц, будут иметь вид 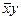и 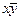. Беря их логическую сумму, получим

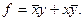
Согласно второму методу, рассматриваем строки, в которых функция равна нулю. Это будут первая и последняя строки функции 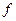. Логические формулы, соответствующие этим строкам, будут иметь вид 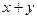и . Беря их логическое произведение, получим

При записи функции выбирают тот метод, для которого меньше соответствующих символов (единиц или нулей).

После представления логической функции в форме канонической суммы или в форме канонического произведения приступают к ее упрощению – минимизации.

Дата добавления: 2014-11-20