Критерий «восходящих» и «нисходящих» серий

Этапы реализации метода:

· Последовательно сравниваются каждое следующее значение e_t+1 с предыдущим и ставится знак «+» или «-»:

e_t+1 > e_t – «+»

e_t+1 < e_t – «-»

e_t+1 = e_t – учитывается только одно наблюдение (другие опускаются).

· Определяется kmax(n) – длина наибольшей серии.

· Определяется V(n) – общее число серий.

· Выдвигается и проверяется гипотеза H0: о случайности выборки и подтверждается, если выполняются следующие неравенства (a = 0,05):

; (2.38)

где:

k₀(n) – определяется следующим образом:

N	k0(n)
n £ 26
26 < n £ 153
153 < n £ 1170

Если хотя бы одно из неравенств не выполняется, то гипотеза о случайном характере отклонений уровней временного ряда от тренда отвергается.

Пример. Произведем оценку случайности отклонений эмпирических значений числа зарегистрированных разбоев от теоретических, полученных по уравнениям линейного тренда и параболы второго порядка.

В качестве примера рассмотрим отклонения от линейного тренда.

Расчет параметров линейного тренда был произведен ранее и получено уравнение тренда:

.

Определим отклонения эмпирических значений признака от теоретических, полученных по уравнению тренда.

Последовательно сравним каждое следующее значение ε_t с предыдущим:

· если , то ставится «+»;

· если 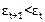ставится «–».

Результат отразим в таблице.

Таблица 2.20

Расчетная таблица критерия «восходящих» и «нисходящих»
серий (по отклонениям от линейного тренда)

Год	yt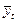
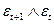
	16,5	21,93	-5,43
	18,5	24,25	-5,75	-
	30,4	26,57	3,83	+
	34,2	28,89	5,31	+
	37,9	31,21	6,69	+
	37,7	33,53	4,17	-
	34,6	35,85	-1,25	-
	34,3	38,17	-3,87	-
	38,5	40,49	-1,99	+
	41,1	42,81	-1,71	+

Выдвигается гипотеза H₀ : о случайности отклонений в ряду динамики.

Для проверки выдвинутой гипотезы определим:

· длину наибольшей серии ;

· число серий V(n)=4;

· при n<26 K₀(n)=5.

Гипотеза не отвергается, если справедлива следующая система неравенств:

.

Оба неравенства выполняются, следовательно гипотеза о случайности отклонений уровней ряда динамики числа зарегистрированных разбоев от линейного тренда не отвергается.

В качестве примера рассмотрим оценку случайности отклонений эмпирических значений числа зарегистрированных разбоев от теоретических, полученных по уравнению параболы второго порядка .

Расчет параметров параболы был произведен ранее и получено уравнение тренда .

Последовательно сравним каждое следующее значение ε _t с предыдущим:

· если ε_t+1 > ε _t, то ставится «+»;

· если ε_t+1 < ε _t, ставится «–». Результат отразим в таблице 2.21.

Таблица 2.21

Расчетная таблица критерия «восходящих» и «нисходящих»
серий (по отклонениям от параболы второго порядка)

Год	yt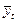
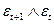
	16,5	16,65	-0,15
	18,5	22,49	-3,99	–
	30,4	27,45	2,95	+
	34,2	31,53	2,67	–
	37,9	34,73	3,17	+
	37,7	37,05	0,65	–
	34,6	38,49	-3,89	–
	34,3	39,05	-4,75	–
	38,5	38,73	-0,23	+
	41,1	37,53	3,57	+

Выдвигается гипотеза H₀: о случайности отклонений эмпирических значений числа зарегистрированных разбоев от теоретических, полученных по уравнению второго порядка.

Для проверки выдвинутой гипотезы определим:

· длину наибольшей серии ;

· число серий V(n)=6;

· при n<=26 K₀(n)=5.

Гипотеза не отвергается, если справедлива следующая система неравенств.

.

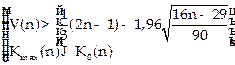
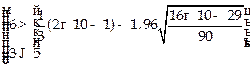
Оба неравенства выполняются, гипотеза о случайности отклонений уровней ряда динамики от параболы второго порядка не отвергается.

Критерий восходящих и нисходящих серий показал случайность отклонений уровней временного ряда от тренда в виде прямой и в виде параболы.

Дата добавления: 2014-12-08