Принадлежность элементов списку

Списки

Список - довольно широко используемая структура данных в области числового программирования. Список -это упорядоченная последовательность элементов, которая может иметь произвольную длину. Признак упорядоченный указывает на то, что порядок элементов в последовательности является существенным. Элементами списка могут быть любые термы – константы, переменные, структуры, которые включают, конечно, и другие списки. Указанные свойства очень полезны в ситуации, когда мы не в состоянии заранее предсказать, насколько большим должен быть список и какую информацию он будет содержать. Более того, списки позволяют представить практически любой тип структуры, который может потребоваться при символьных вычислениях. Списки широко используются для представления деревьев синтаксического разбора, грамматик, карт городов, программ для ЭВМ и математических объектов, таких как графы, формулы и функции. Существует язык программирования – Лисп, в котором единственными доступными структурами данных являются константа и список. Однако в Прологе список – это просто один из частных видов структуры.

Списки могут быть представлены как специального вида дерево. Список – это любой пустой список, не содержащий ни одного элемента, либо структура, имеющая две компоненты: голову и хвост списка. Конец списка обычно представляют как хвост, который является пустым списком. Пустой список записывают как [] – открывающая квадратная скобка, за которой следует закрывающая квадратная скобка. Голова и хвост списка являются компонентами функтора, обозначаемого точкой '.'. Так, список, состоящий из одного элемента ' а ' есть .(а, []), а его представление в виде дерева имеет вид

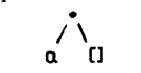
Аналогично список, состоящий из атомов a, b и с, мог бы быть записан как .(а,.(b,.(с,[]))), что изображается следующим образом:

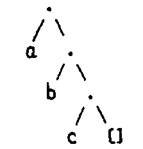
Иногда функтор точка ('.') определяется как оператор, так что допустимо для Пролога два последних списка записать как а.[] и а.(b.(с.[]))). Второй список можно было бы записать просто как а.b.с.[], так как функтор точка – правоассоциативный оператор. Списки являются упорядоченными последовательностями элементов, так что список а.b отличается от списка b.а.

Некоторые любят записывать древовидные диаграммы списков в виде дерева, «растущего» слева направо, ветви которого направлены вниз. Приведенный выше список, представленный диаграммой в виде такой «виноградной лозы» выглядит так:

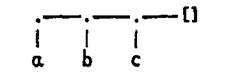
В этой диаграмме компонента функтора '.', соответствующая голове списка, «свисает» вниз, а компонента, соответствующая хвосту списка, «растет» вправо. Конец списка четко выделен тем, что последняя компонента – хвост списка – является пустым списком. Главное преимущество использования диаграммы для представления списка заключается в том, что она может быть записана справа налево на листе бумаги.

«Виноградная» диаграмма может оказаться удобной для записи списков на бумаге, когда нам необходимо видеть структуру списка, но в программах на Прологе для записи списков такие диаграммы не используются. Так как запись сложных списков с помощью функтора '.' часто оказывается неудобной, то в Прологе предусмотрена другая синтаксическая форма, которая может быть использована для записи списков в программе. Это так называемая скобочная форма записи списка. Она представляет собой заключенную в квадратные скобки последовательность элементов списка, разделенных запятыми. Например, упоминавшиеся выше списки могут быть записаны в скобочной форме в виде [а] и [а, b, с]. Списки могут содержать другие списки или переменные. Например, в Прологе допустимы следующие списки:

[]

[конкретный, человек, [любит, ловить, рыбу]]

[а, V1, b, [X, Y]]

Переменные, входящие в списки, ничем не отличаются от переменных в любой другой структуре. Они в любой момент могут быть конкретизированы, так что умелое использование переменных может обеспечить образование «пустых мест» в списке, которые впоследствии могут быть заполнены данными.

Чтобы продемонстрировать структуру списков, содержащих в качестве элементов другие списки, приведем «виноградную» диаграмму для последнего из рассмотренных списков:

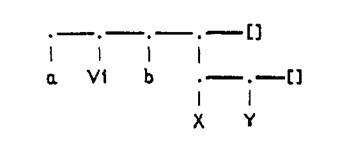
Из приведенной диаграммы ясно видно, что каждый ее горизонтальный уровень является списком, состоящим из некоторого числа элементов. Верхний уровень на приведенной диаграмме представляет список, содержащий четыре элемента, один из которых сам является списком. Второй уровень, содержащий два элемента, представляет четвертый элемент списка верхнего уровня. Работа со списками основана на расщеплении их наголову и хвост списка. Голова списка – это первый аргумент функтора '.', который используется для конструирования списка. Хвост списка – это второй аргумент функтора '.'. В случае когда для записи списка используется скобочная форма записи, головой списка является первый его элемент. Хвост списка представляет список, состоящий из всех элементов исходного списка, за исключением первого его элемента. Следующие примеры демонстрируют расщепление списков на голову и хвост:

Список	Голова	Хвост
[а, b, с]	а	[b, с]
[а,]	а	[]
[]
[[эта, кошка], сидела]	[эта, кошка]	[сидела]
[эта, [кошка, сидела]]	эта	[кошка, сидела]]
[эта, [кошка, села], на пол]	эта	[кошка, села], на пол]
[X+Y, х + y]	X + Y	[x + y]

Заметим, что пустой список не имеет ни головы, ни хвоста. В последнем примере оператор ± используется как функтор для структур +(Х, Y) и +(х,у).

Так как операция расщепления списка на голову и хвост очень широко используется, то в Прологе введена специальная форма для представления списка с головой X и хвостом Y. Это записывается как [X|Y], где для разделения X и Y используется вертикальная черта. При конкретизации структуры подобного вида X сопоставляется с головой списка, a Y – с хвостом списка, как это показано в следующем примере:

p([1, 2, 3]).

p([эта, кошка, сидела, [на, этой, подстилке]]).

?- p([X|Y]).

X = 1 Y=[2,3] ;

X=эта Y=[кошка, сидела, [на, этой, подстилке]]

?- p([_,_,_,[_|X]]).

X=[этой, подстилке]

Ниже приведено еще несколько примеров с использованием различных синтаксических возможностей записи списков, показывающих, каким образом производится сопоставление списков. В этих примерах делается попытка сопоставить два заданных списка, конкретизируя переменные, если это возможно.

Список 1	Список 2	Конкретизация
[X, Y, Z]	[джону,нравится,рыба]	X=джону Y= нравится Z = рыба
[кошка]	[X| Y]	X= кошка
[X, Y | Z]	[мэри,нравится,вино]	X = мэри Y = нравится Z = [вино]
[[этот, Y]|Z]	[[X, заяц], [находится, здесь]]	X = этот Y = заяц Z = [[находится_ здесь]]
[X, Y|Z, W]	(синтаксически некорректная конструкция списка)
[золотистый | T]	[золотистый, норфолк]	T= [норфолк]
[лошадь, X]	[белая, лошадь]	(сопоставление невозможно)
[белая | Q]	[P | лошадь]	P = белая Q = лошадь

Как видно из последнего примера, используя скобочную форму записи списков, можно создавать структуры, похожие на списки, но не заканчивающиеся пустым списком. Одна из таких структур, [белая|лошадь], обозначает структуру, головой которой является белая, а хвостом – лошадь. Константа лошадь не является ни списком, ни пустым списком, и, как мы увидим далее, обработка таких структур требует большой осторожности, когда они используются в качестве хвоста списка.

Существует еще одна область применения списков – это представление строк литер. Иногда возникает необходимость в использовании строк литер для печати или ввода текста. Если строка литер заключена в двойные кавычки, то эта строка представляется как список кодов, соответствующих литерам строки. Для кодировки литер используется код ASCII, который обсуждался в разд. 2.2. Например, строка "system" преобразуется в Прологе в следующий список: [115, 121, 115, 116, 101, 109].

Предположим, что имеется некоторый список, в котором X обозначает его голову, a Y – хвост списка. Напомним, что такой список мы можем записать так: [X|Y]. Этот список мог бы содержать, например, клички тех лошадей потомков жеребца Coriander, которые все выиграли скачки в Великобритании в 1927 году:

[curragh_tip, music_star, park_mill, portland]

Теперь предположим, что мы хотим определить, содержится ли некоторая кличка в указанном списке. В Прологе это можно сделать, определив, совпадает ли данная кличка с головой списка.

Если совпадает, то наш список завершается успехом. Если нет, то мы проверяем, есть ли кличка в хвосте исходного списка. Это значит, что снова проверяется голова, но уже хвоста списка. Затем проверяется голова очередного хвоста списка. Если мы доходим до конца списка, который будет пустым списком, то наш поиск завершается неудачей: указанной клички в исходном списке нет.

Для того чтобы записать все это на Прологе, сначала надо установить, что между объектом и списком, в который этот объект может входить, существует отношение. Это отношение, называемое отношением принадлежности, представляет достаточно распространенное в повседневной жизни понятие. Так, мы говорим о людях, являющихся членами клубов, и о других тому подобных вещах. Для записи этого отношения мы будем использовать предикат принадлежит: целевое утверждение принадлежит(X, Y) является истинным («выполняется»), если терм, связанный с X, является элементом списка, связанного с Y. Имеются два условия, которые надо проверить для определения истинности предиката. Первое условие говорит, что X будет элементом списка Y, если X совпадает с головой списка Y. На Прологе этот факт записывается следующим образом:

принадлежит(X,[X |_]).

Эта запись констатирует, что X является элементом списка, который имеет X в качестве головы. Заметим, что мы использовали анонимную переменную '_' для обозначения хвоста списка. Это сделано потому, что мы никак не используем хвост списка в этом частном факте. Заметим, что данное правило могло бы быть записано и по-другому:

принадлежит(X,[Y|_]:- X = Y.

К этому моменту вы должны уже понимать, почему можно использовать X сразу в двух местах в первой, более короткой, версии этого правила.

Второе, и последнее, правило говорит о том, что X принадлежит списку при условии, что он входит в хвост этого списка, обозначаемый через Y. И нет лучшего пути, чем использовать тот же самый предикат принадлежит для того, чтобы определить, принадлежит ли X хвосту списка! В этом и состоит суть рекурсии. На Прологе это выглядит так:

принадлежит(X,[_ |Y]):- принадлежит(X,Y).

и констатирует, что X является элементом списка, если X является элементом хвоста этого списка. Заметим, что мы использовали анонимную переменную '_', так как нас не интересует имя переменной, обозначающей голову списка. Два этих правила в совокупности определяют предикат для отношения принадлежности и указывают Прологу, каким образом просматривать список от начала до конца при поиске некоторого элемента в списке. Наиболее важный момент, о котором следует помнить, встретившись с рекурсивно определенным предикатом, заключается в том, что прежде всего надо найти граничные условия и способ использования рекурсии.

Для предиката принадлежит в действительности имеются два типа граничных условий. Либо объект, который мы ищем, содержится в списке, либо он не содержится в нем. Первое граничное условие для предиката принадлежит распознается первым утверждением, которое приведет к прекращению поиска в списке, если первый аргумент предиката принадлежит совпадает с головой списка, соответствующего второму аргументу. Второе граничное условие встречается, когда второй аргумент предиката принадлежит является пустым списком.

Как мы можем убедиться в том, что граничные условия будут когда-либо удовлетворены? Для этого необходимо обратить внимание на то, как используется рекурсия во втором правиле для предиката принадлежит. Заметим, что каждый раз, когда при поиске соответствия для целевого предиката принадлежит происходит рекурсивное обращение к тому же предикату, новая цель формируется для более короткого списка. Хвост списка всегда является более коротким списком, чем исходный список. Очевидно, что рано или поздно произойдет одно из двух событий: либо произойдет сопоставление с первым правилом для принадлежит, либо в качестве второго аргумента принадлежит будет задан список длины 0, т. е. пустой список. Как только возникнет одна из этих ситуаций, прекратится рекуррентное порождение целей для предиката принадлежит. Первое граничное условие распознается фактом, который не вызывает порождения новых подцелей. Второе граничное условие не распознается ни одним из утверждений для принадлежит, так что процесс поиска сопоставимого элемента списка для целевого утверждения принадлежит закончится неудачей. Это демонстрирует следующий пример на Прологе:

принадлежит(Х, [X | _]).

принадлежит(Х,[_|Y]):- принадлежит (X,Y).

?- принадлежит(d,[a,b,с,d,e,f,g]).

да

?- принадлежит(2,[3,a,4,f]).

нет

Предположим, мы введем вопрос

?- принадлежит(clugatе,[curraugh_tiр,music_star,раrk_mill, ortland]).

Так как clygate не сопоставимо с curragh_tip, то происходит сопоставление со вторым правилом для принадлежит. Переменная Y получает значение [music_star, park_mill, portland], и порождается следующая цель: определить, принадлежит ли clygate этому списку. Опять происходит сопоставление со вторым правилом, и снова выделяется хвост списка. Текущей целью становится принадлежит (clugate,[park_mill,portland]) Этот процесс рекурсивно повторяется до тех пор, пока мы не доберемся до цели, у которой X есть clygate, a Y есть [portland]. Происходит еще одно сопоставление со вторым правилом, и теперь Y конкретизируется хвостом списка [portland], который является пустым списком. Следующей целью становится принадлежит(clygate,[]). Ни одно из правил в базе данных не сопоставимо с этой целью, так что цель оказывается ложной и ответ на вопрос будет отрицательным.

Важно помнить, что каждый раз, когда при согласовании принадлежит с базой данных выбирается второе утверждение этого предиката, Пролог рассматривает рекурсивное обращение к предикату принадлежит как попытку найти соответствие для некоторой новой его «копии». Это предотвращает путаницу переменных, соответствующих одному употреблению утверждения, с переменными, соответствующими другому употреблению этого же утверждения.

Предикат отношения принадлежности настолько полезен, что мы еще неоднократно будем использовать его в оставшейся части этой книги. Предикат принадлежит важен еще и потому, что он представляет практически наименьший полезный пример рекурсивного предиката – определение предиката принадлежит содержит утверждения, которые могут быть проверены с помощью только того же самого предиката принадлежит. Рекурсивные определения часто встречаются в программах на Прологе, и они полностью равноправны с другими определениями. Однако надо быть осторожным, чтобы не допускать «закольцованные» определения, как, например, следующее:

родитель(X,Y):- ребенок(Y,X).

ребенок(A,B):- родитель(B,A).

В этом примере, чтобы согласовать с базой данных целевое утверждение родитель, необходимо согласовать подцель ребенок. Однако определение для ребенок приведет к появлению единственной подцели – родитель. Вы должны понимать, почему вопрос, содержащий в качестве целей родитель или ребенок, приводит к циклу, находясь в котором Пролог не сможет найти какие-либо новые факты, и этот цикл никогда не завершится.

Одна важная проблема, на которую следует обращать внимание в рекурсивных определениях, - это левосторонняя рекурсия. Она возникает в случае, когда правило порождает подцель, по существу эквивалентную исходной цели, которая явилась причиной использования этого правила. Так, если бы мы определили предикат

человек(X):- человек(Y), мать(Х,Y).

человек(адам).

и ввели вопрос

?- человек(X).

то Пролог сначала использовал бы правило и рекурсивно породил подцель человек (Y). Попытка найти соответствие этой цели вновь привела бы к выбору первого правила и породила бы еще одну новую эквивалентную подцель. И так далее, до тех пор, пока не исчерпались бы вычислительные ресурсы. Конечно, если бы была возможность использовать механизм возврата, то был бы найден сообщенный в определении факт об Адаме и началось бы порождение решений^[7]. Ошибка заключается в том, что для того, чтобы начался возврат, Пролог должен потерпеть неудачу при проверке первого утверждения. В данном же случае поиск решения оказывается неопределенно длинным, и нет никакой возможности завершить этот поиск с успехом либо с неудачей. Из всего сказанного выше можно извлечь следующую мораль:

Не следует предполагать, что только потому, что вы предоставили все относящиеся к делу факты и правила, Пролог всегда найдет их. Создавая программу на Прологе, вы все время должны представлять, каким образом Пролог осуществляет поиск в базе данных и какие переменные будут конкретизированы, когда будет использовано одно из ваших правил.

Для приведенного примера имеется простой способ устранения ошибки – поместить факт перед правилом, а не после него. В действительности существует хороший эвристический принцип: помещать, где это возможно, факты перед правилами. Иногда при размещении правил в некотором конкретном порядке может возникнуть ситуация, когда они будут правильно работать для целей одного вида и не будут работать для целей другого вида. Рассмотрим следующее определение предиката список (X), при котором предикат список является истинным, если X – список, последний элемент которого имеет в качестве хвоста пустой список:

список([A|B]):- список(B).

список([]).

Если мы используем эти правила для получения ответов на вопросы, подобные следующим:

?- список ([a,b,c,d]).

?- список([]).

?- список(f(1,2,3))

то данное определение будет работать хорошо. Но если мы сделаем запрос

?- список(X).

то программа зациклится. Предикат, аналогичный предикату список, но неподверженный зацикливанию, задается следующими двумя фактами:

обобщенный_список([]).

обобщенный_список([_ |_]).

В этом варианте просто проверяется начало списка, а не тот факт, что последний хвост списка является пустым списком ([]). Последнее определение не является таким же строгим тестом правильности списка, как определение предиката список, но оно не приведет к зацикливанию, если аргументом является переменная.

3.4. Пример: преобразование предложений

Рассмотрим программу на Прологе, которая в ответ на введенное с терминала предложение (на английском языке) печатает другое предложение, представляющее преобразованное исходное предложение. Эта программа для «ответов» программисту могла бы поддерживать следующий диалог:

Вы: you are a computer (Вы - ЭВМ)

Пролог: i am not a computer (Я – не ЭВМ)

Вы: do you speak french (Вы говорите по-французски?)

Пролог: no i speak german (Нет, я говорю по-немецки)

Хотя этот диалог может показаться натянутой, но все же осмысленной беседой, очень легко написать программу, выполняющую свою «часть» диалога. Для этого достаточно просто последовательно выполнять следующие действия:

1. Ввести предложение, набранное пользователем на терминале.

2. Заменить каждое вхождение слова you на слово i.

3. Аналогичным образом заменить are на am not.

4. Заменить french на german.

5. Заменить do на nо.

Если применить данную схему преобразования к надлежащим образом подобранным предложениям, подобным использованным в приведенном выше диалоге, то получим осмысленные преобразованные предложения. Однако эта схема применима не ко всем предложениям. Например;

Вы: i do like you (я действительно люблю вас)

Пролог: i no like i (я не люблю себя)

Но если простая программа уже написана, то впоследствии ее можно модифицировать так, чтобы она справлялась и с предложениями, подобными приведенному.

Программа на Прологе, преобразующая одно предложение английского языка в другое, может быть реализована следующим образом. Прежде всего необходимо осознать, что имеется отношение между исходным предложением и преобразованным. В связи с этим нам следует определить предикат, называемый преобразовать. Преобразовать(Х, Y) означает, что предложение X может быть преобразовано в предложение Y. Предложения X и Y удобно представлять в виде списков атомов, обозначающих слова, так что предложения могут быть записаны следующим образом: [this,is,a, sentence] (это некоторое предложение). Определив предикат преобразовать, мы могли бы обращаться к Прологу с вопросами вида

?- преобразовать([dо,you,know,french],X). (Знаете ли вы французский)

на что Пролог отвечал бы

X=[no,i,know,german] (нет, я знаю немецкий).

Не следует обращать внимание на то, что вводимое и печатаемое в ответ предложения представлены в такой неестественной форме и не похожи на обычные предложения. В последующих главах мы обсудим способы ввода и вывода структур в виде, удобном для чтения. В данный момент нас интересуют лишь способы преобразования одного списка в другой.

Так как аргументами предиката преобразовать являются списки, то прежде всего следует рассмотреть, что произойдет, если исходный список пустой. В этом случае мы скажем, что пустой список преобразуется в пустой список:

преобразовать([], [])

Или, иначе: это факт, что преобразование пустого списка дает пустой список. Если причины для того, чтобы рассматривать пустой список, здесь не очевидны, то последующее изложение прояснит их. Далее нам следует разобраться в том, что основные действия предиката преобразовать заключаются в следующем:

1. Заменить голову входного списка соответствующим словом и поместить это слово в выходной список в качестве головы.

2. Преобразовать хвост входного списка и сделать его хвостом выходного списка.

3. Если мы достигли конца входного списка, то к выходному списку больше ничего добавлять не надо, и мы можем завершить выходной список пустым списком [].

Переводя это на язык, более близкий к Прологу, можно сказать:

Преобразование списка с головой H и хвостом T дает список с головой X и хвостом Y, если замена слова H дает слово X, а преобразование списка T дает список Y.

Теперь следует сказать, что значит «заменить» одно слово на другое. Это может быть сделано при наличии в базе данных фактов вида заменить(Х, Y), означающих, что слово X может быть заменено словом Y. В конце базы данных следует поместить факт-«ловушку», так как если слово не заменяется другим словом, то его следует заменить самим собой. Если сейчас не совсем понятно назначение «ловушки», то позднее, когда мы объясним, как работает программа, это должно стать ясным.

Роль такого факта-ловушки выполняет факт заменить(Х,Х), который обозначает, что слово X заменяется самим собой. Ниже приведена база данных, обеспечивающая указанные выше замены слов:

заменить(уоu,i).

заменить(аrе, [am,not]).

заменить(french,german).

заменить(dо,nо)

заменить(Х,Х). /* это факт-ловушка */

Заметим, что фраза «am not» представлена как список, так что она входит в факт как один аргумент.

Теперь можно перевести приведенный выше текст на псевдо-Прологе в настоящую программу на Прологе, помня, что запись [А|В] обозначает список, имеющий голову А и хвост В. Мы получаем нечто подобное следующему:

преобразовать([],[]).

преобразовать([Н|T],[X|Y]):-заменить(Н, X), преобразовать(Т,Y).

Первое утверждение в приведенной процедуре проверяет, является ли аргумент пустым списком. Оно же проверяет окончание списка. Как? Рассмотрим это на примере:

?- преобразовать([уоu,are,a,computer],Z).

Этот вопрос был бы сопоставлен с основным правилом для преобразовать, при этом переменная Н получила бы значение you, а переменная Т – значение [are,a,computer]. Затем была бы рассмотрена подцель заменить (you,Х), найден подходящий факт и переменная X стала бы равной i. Так как X является головой выходного списка (в целевом утверждении преобразовать), то первое слово в выходном списке есть i. Далее, поиск соответствия для подцели преобразовать ([are, a, computer], Y) привел бы к использованию того же правила. Слово are в соответствии с имеющейся базой данных заменяется на список [am,not], и генерируется другая подцель с предикатом преобразовать – преобразовать([а,computer], Y). Ищется факт заменить(а,X), но так как в базе данных нет факта заменить, первый аргумент которого равен а, то будет найден факт-ловушка, расположенный в конце базы данных, заменяющий ' а ' на ' а '. Правило преобразовать вызывается еще раз с computer в качестве головы входного списка и пустым списком [] в качестве хвоста входного списка. Как и ранее, заменить(computer, X) сопоставляется с фактом-ловушкой. Наконец, преобразовать вызывается с пустым списком на месте первого аргумента, и происходит сопоставление с первым утверждением предиката преобразовать. Результатом является пустой список, который заканчивает преобразованное предложение (напомним, что список заканчивается пустым хвостом). В заключение Пролог отвечает на вопрос, печатая

Z = [i,[am,not], a, computer]

Отметим, что фраза [am,not] появляется в списке точно в таком же виде, как она была в него вставлена.

Теперь должны быть ясны причины появления в базе данных факта преобразовать ([],[]) и факта-ловушки заменить (Х,Х). Факты, подобные этим, часто включаются в программу, когда требуется проверить выполнение граничных условий. Из приведенного выше объяснения должно быть ясно, что выход на граничные условия происходит в случае, когда входной список становится пустым и когда оказываются просмотренными все факты для предиката заменить. В обоих случаях выхода на граничные условия необходимо выполнить определенные действия. В случае когда входной список становится пустым, необходимо завершить выходной список (вставив пустой список в его конец). Если просмотрены все факты для предиката заменить, но при этом не обнаружен факт, содержащий данное слово, то это слово должно остаться неизменным (путем замены его самим собой).

3.5. Пример: упорядочение по алфавиту

Как мы видели в гл. 2, в Прологе существуют предикаты для сравнения целых чисел. В приложениях, имеющих дело со словами, например работа со словарями, полезно иметь предикат для сравнения слов в соответствии с алфавитным порядком.

Рассмотрим предикат, который мы назовем меньше. Если предикат меньше(Х, Y) используется в качестве целевого утверждения, то он истинен (т. е. согласуется с базой данных), если X и Y обозначают атомы и X по алфавиту предшествует Y. Так, предикат меньше(арбуз, букварь) истинен, а меньше(ветер,автомобиль) ложен. Точно так же должен быть ложен и предикат меньше(картина,картина). Сравнивая два слова, мы сравниваем их последовательно, буква за буквой и при сравнении каждой буквы определяем, какое из следующих условий имеет место:

1. Достигнут конец первого слова, но не достигнут конец второго слова. Это имеет место, например, в случае меньше(пар, паровоз). При возникновении такой ситуации предикат меньше должен считаться истинным (т. е. согласованным с базой данных).

2. Очередная литера в первом слове предшествует в алфавите соответствующей литере во втором слове. Например, меньше (слово,слон). Буква ' в ' в слове слово предшествует в алфавите букве ' н ' в слове слон. В этом случае предикат меньше истинен.

3. Литера в первом слове совпадает с соответствующей литерой во втором слове. В этом случае следует использовать предикат меньше для сравнения оставшихся литер в обоих словах. Например, если дано меньше(облако,одеяло), то, так как оба аргумента начинаются с буквы ' о ', необходимо взять в качестве следующей цели меньше(блако,деяло).

4. Одновременно достигнут конец первого и второго слов, как, например, в случае меньше(яблоко,яблоко). При возникновении такого условия предикат меньше должен быть ложным, так как оба слова являются одинаковыми.

5. Обработаны все литеры второго слова, но еще остались литеры в первом слове, как, например, в случае меньше(алфавитный,алфавит). В такой ситуации предикат меньше должен быть ложным.

После того как сформулированы перечисленные выше условия, задача перевода их на Пролог является довольно простой. Будем представлять слова в виде списков литер (целых чисел из некоторого диапазона). Для этого необходим способ преобразования атома в список литер. Эту функцию выполняет встроенный предикат Пролога name(имя). Целевое утверждение name(X, Y) согласуется с базой данных, когда атом, являющийся значением X, состоит из литер, коды которых образуют список, являющийся значением Y (используются коды ASCII). Отсылаем читателя к гл. 2, если он забыл, что такое коды ASCII. Если один из аргументов не определен, то Пролог предпримет попытку конкретизировать его, создавая соответствующую структуру. Поэтому можно использовать предикат name для преобразования слова в список литер. Например, зная, что код ASCII для 'а' есть 97, код для 'l' – 108 и код для 'p' – 112, можно задавать следующие вопросы:

?- name (Х,[97,108,112])

Х=аlр

?- name (alp,X)

X=[97,108,112]

Первым утверждением в определении предиката меньше является следующее правило:

меньше(Х, Y):- name(X,L),name(Y,M), меньше_l(L,M)

Это правило сначала преобразует слова в списки, используя предикат name, и затем с помощью предиката меньше_1 (будет определен ниже) сравнивает списки на соответствие алфавиту. Определение предиката меньше_1 состоит из утверждений, реализующих приведенный выше набор условий. Первое условие является истинным, когда первый аргумент есть пустой список, а второй аргумент – это произвольный непустой список:

меньше_1([], [_|_]).

Второе условие записывается следующим образом:

меньше_1([X|_],[Y|_]):- X‹Y

Напомним, что аргументами предиката меньше_1 являются списки чисел, так что разрешается сравнивать элементы этих списков, используя предикат '‹'. Третье условие записывается следующим образом:

меньше_1([А|Х],[В|Y]:- А=В, меньше_1(Х,Y).

Наконец, два последних условия описывают ситуации, когда предикат ложен, т. е. не согласуется с базой данных, так что если мы не предусмотрим никаких соответствующих им фактов или правил, то при используемом механизме поиска в базе данных доказательство согласованности любого целевого утверждения, для которого эти условия справедливы, закончится неудачей. Собирая все правила вместе, получим

меньше(Х,Y):- name(X,L), name(Y,M), меньше _1(L,M).

меньше_1([], [_|_]).

меньше_1([X|_],[Y|_]):- Х‹Y.

меньше_1([P|Q], [R|S]):- P = R, меньше_1(Q,S).

Заметим, что третье правило для меньше_1 можно было бы записать более естественно так:

меньше_1([H|Q], [H|S]):- меньше_l(Q,S).

Упражнение 3.1. Подумайте, какое еще утверждение необходимо добавить к этому определению так, чтобы предикат был истинен и в том случае, когда два слова совпадают. В результате получится предикат, проверяющий, меньше или равен первый аргумент второму по алфавиту. Указание: обратите внимание на условие (4), приведенное выше, и вставьте утверждение, обрабатывающее это условие.

Упражнение 3.2. Почему в первом утверждении для предиката меньше_1 в качестве второго аргумента использован список [_|_]? Почему недостаточно использовать список [.]?

Дата добавления: 2014-12-08