Установление соответствия

Рассмотрение целевых утверждений при использовании механизма возврата

Успешное доказательство конъюнкции целевых утверждений

Общая схема согласования целевых утверждений

Для ответа на вопрос, поступивший от программиста, Пролог выполняет решение некоторой задачи. Вопрос содержит конъюнкцию целевых утверждений, которые необходимо попытаться доказать, т. е. проверить на согласованность с базой данных. Для доказательства целевых утверждений Пролог использует известные утверждения. Факт может привести к немедленному доказательству (согласованию) целевого утверждения, в то время как правило может только свести данную задачу к конъюнкции предикатов-подцелей. Однако использование некоторого утверждения возможно только, когда оно «подходит» к рассматриваемому целевому утверждению, т. е. соответствует ему (сопоставимо с ним). Если целевое утверждение не доказано, возбуждается процесс возврата. Процесс возврата заключается в пересмотре проделанной работы и попытках передоказать (вновь согласовать) целевые утверждения путем поиска альтернативных путей доказательства. Более того, если программист неудовлетворен ответом на свой вопрос, он может сам инициировать процесс возврата, нажав на клавиатуре клавишу ';', после того как Пролог информирует его о найденном решении. В данном разделе будут представлены диаграммы, показывающие, как Пролог пытается доказать и передоказать целевые утверждения.

Пролог пытается согласовать с базой данных входящие в конъюнкцию целевые утверждения в том порядке, в каком они написаны (слева направо), где бы они ни появились – в теле правила или в вопросе. Это означает, что Пролог не будет проверять некоторое утверждение, пока не будет доказан его сосед слева. А сосед справа будет рассматриваться только после доказательства данного целевого утверждения. Рассмотрим следующую простую программу о семейных связях:

родители (С,M,F):- мать(С,М), отец(C,F).

мать(джон,анна).

мать(мэри,анна).

отец(мэри,фред). отец(джон,фред).

Давайте рассмотрим последовательность событий, позволяющую дать ответ на вопрос:

?-женщина(мэри), родители(мэри,М,Р), родители(джон,М,Р).

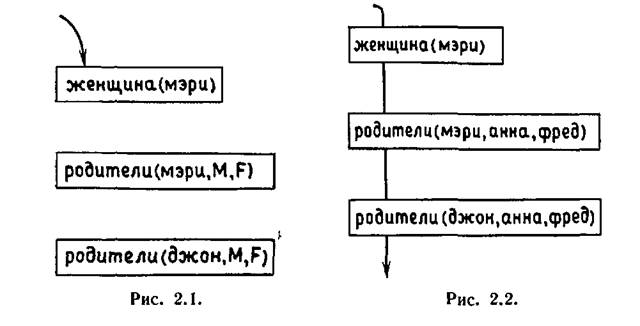
Данный вопрос позволяет определить, является ли мэри сестрой джона. Для того чтобы дать ответ Прологу, необходимо согласовать с базой данных последовательность подцелей, приведенных на рис. 2.1.

Представим целевые утверждения в виде прямоугольников, распределенных по странице. Стрелка, начинающаяся в верхней части страницы, указывает, какие целевые утверждения уже согласованы. Прямоугольники, через которые стрелка уже прошла, соответствуют согласованным целевым утверждениям. Прямоугольники, лежащие ниже острия стрелки, соответствуют целевым утверждениям, которые Пролог еще не рассматривал. При выполнении программы стрелка движется вверх и вниз по странице в соответствии с переходом Пролога от одного целевого утверждения к другому. Будем называть ее цепочкой доказательств. В данном примере стрелка начинается в верхней части страницы, как показано выше. По мере согласования трех целевых утверждений она будет удлиняться вниз, проходя через соответствующие прямоугольники. Конечная ситуация представлена на рис. 2.2. Отметим, что в ходе доказательства согласованности целевых утверждений с базой данных были найдены значения для переменных М и F.

Такая диаграмма иллюстрирует общую структуру происходящего, но она не показывает, как доказывались эти три целевых утверждения. Для того чтобы показать это, поместим внутрь прямоугольников больше информации. Давайте посмотрим, как доказывалось второе целевое утверждение. Доказательство согласованности целевого утверждения с базой данных включает в себя поиск в базе данных соответствующих (сопоставимых) утверждений, пометку этого места базы данных и затем доказательств возникших подцелей. Этот процесс для второго целевого утверждения можно проиллюстрировать, включив в прямоугольник родители индикацию выбранного утверждения и возникшие подцели. Выбранное утверждение обозначается числом в скобках, в данном случае (1). Это число указывает номер выбранного утверждения в наборе утверждений с соответствующим предикатом. Таким образом, число 1 означает, что было выбрано первое утверждение с данным предикатом. Эта информация достаточна для отметки места в базе данных. Подцели заключены в маленькие прямоугольники, помещенные в прямоугольник данного целевого утверждения. В момент, когда выбрано утверждение родители, ситуация выглядит так, как показано на рис. 2.3.

Рис. 2.3.

Стрелка вошла в прямоугольник родители и прошла через скобки, указывая, что выбрано некоторое утверждение. Данное утверждение создало две подцели – мать и отец. В данный момент для получения ответа на вопрос необходимо, чтобы стрелка прошла через два маленьких прямоугольника, вышла из прямоугольника родители и затем прошла через второй прямоугольник родители. Когда стрелка проходит через маленькие прямоугольники, необходимо выполнить те же самые шаги: выбор соответствующего утверждения и доказательство порождаемых им подцелей. В данном примере для каждого из этих двух целевых утверждений в базе данных находится соответствующий факт, и их согласованность с базой данных доказывается. На рис. 2.4 приведено более детальное изображение ситуации в момент получения ответа на вопрос.

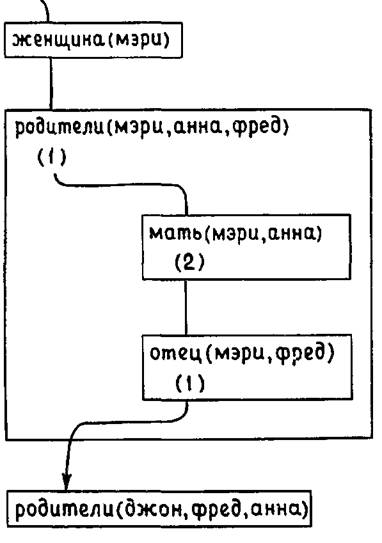
Рис. 2.4.

Отметим, что для полноты картины нам необходимо было бы показать, как доказываются целевые утверждения женщина(мэри) и родители(джон,анна,фред). Однако столь подробная диаграмма не поместилась бы на одной странице.

Данный пример иллюстрирует общую схему рассмотрения целевых утверждений, объединенных в конъюнкцию, для случая, когда все цели согласуются с базой данных. Стрелка перемещается вниз по странице, по очереди проходя через прямоугольники. Когда стрелка входит в какой-либо прямоугольник, выбирается некоторое утверждение и отмечается его позиция. Если данное утверждение сопоставимо с целью и является фактом, стрелка может покинуть прямоугольник (такая ситуация имела место для целевых утверждений мать и отец). Если же утверждение сопоставимо с целью, но является правилом, создаются прямоугольники для подцелей, и стрелка должна пройти через них, прежде чем она сможет покинуть первоначальный прямоугольник.

Когда целевое утверждение недоказуемо (проверены все возможные утверждения или пользователь нажал клавишу ';'), «цепочка доказательств» проходит назад тот путь, по которому она пришла в данную точку. Она возвращается в покинутые перед этим прямоугольники для того, чтобы попытаться передоказать (вновь согласовать) соответствующие целевые утверждения. Когда стрелка возвращается в то место, где было выбрано какое-то утверждение (это событие изображается числом в скобках), Пролог пытается найти альтернативное утверждение, соответствующее данной цели. Сначала делаются неопределенными все переменные, которые были конкретизированы в ходе доказательства данного целевого утверждения. Затем возобновляется поиск в базе данных, начиная с того места, где был оставлен маркер. Если будет найдено другое утверждение, соответствующее целевому, Пролог помечает это место, и дальше события развиваются, как было описано выше в разд. 2.6.1. Отметим, что рассмотрение любых целевых утверждений, находящихся «ниже» данного (даже если они были пройдены в ходе рассмотрения предыдущей альтернативы), всегда начинается с самого начала. Пролог пытается доказать их без учета положения маркера (т. е. это не передоказательство). Если не удается найти другое подходящее утверждение, данное целевое утверждение считается недоказуемым и стрелка продолжает возвращаться назад до следующего маркера. В нашем примере, если целевое утверждение родители(джон,анна,фред) недоказуемо, стрелка уйдет назад из прямоугольника родители(джон,анна,фред) и войдет в прямоугольник родители (мэри,анна,фред) снизу для того, чтобы попытаться передоказать данное целевое утверждение (см. рис. 2.5).

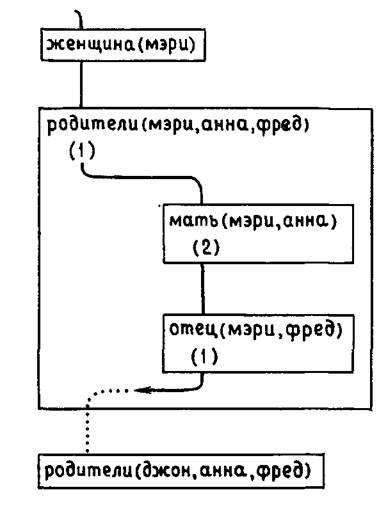
Рис. 2.5.

Отступая дальше, стрелка достигнет места, где было выбрано утверждение, соответствующее целевому утверждению отец. В первую очередь освобождаются все переменные, которые были конкретизированы в результате использования данного утверждения. Это означает, что переменная F вновь становится неконкретизированной. Затем Пролог просматривает базу данных, начиная с утверждения, следующего за первым утверждением с предикатом отец (здесь находится маркер), пытаясь найти альтернативное утверждение. Если предположить, что мэри имеет только одного отца, то этот процесс успехом не завершится. Поэтому стрелка продолжит отступление. Она покинет прямоугольник отец(мэри, F) (это целевое утверждение недоказуемо) и вернется в прямоугольник мать(мэри,анна) (для того, чтобы попытаться передоказать данное целевое утверждение) (см. рис. 2.6).

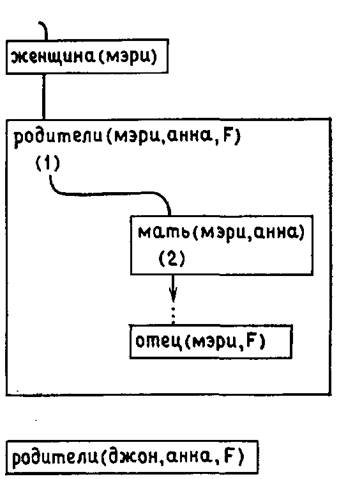
Рис. 2.6.

Отступление стрелки будет продолжаться до успешного доказательства соответствующего целевого утверждения.

Эти примеры иллюстрируют общую схему повторного рассмотрения целевых утверждений в процессе возврата. Когда некоторое целевое утверждение недоказуемо, стрелка возвращается из соответствующего прямоугольника в прямоугольник с предшествующим целевым утверждением. Стрелка отступает до тех пор, пока не встретится маркер. Все переменные, которые были конкретизированы в результате предыдущего выбора сопоставимого утверждения, становятся неконкретизированными. Затем Пролог возобновляет поиск в базе данных сопоставимого утверждения, начиная с маркера. Если сопоставимое утверждение будет найдено, новое место помечается маркером, создаются прямоугольники для целевых подутверждений и стрелка опять начинает движение вниз. В противном случае стрелка продолжает отступать вверх в поисках другого маркера.

Правила, определяющие, подходит ли некоторое утверждение для согласования с целевым утверждением, выглядят следующим образом. Отметим, что при выборе утверждения все переменные сначала неконкретизированы.

• Неконкретизированная переменная соответствует любому объекту. Этот объект становится значением переменной.

• Целое число или атом соответствуют только самим себе.

• Между структурами можно установить соответствие, только если они имеют одинаковый функтор, одинаковое число параметров и соответствующие параметры соответствуют друг другу.

Особым случаем является установление соответствия между двумя неконкретизированными переменными. В этом случае мы говорим, что переменные сцеплены. Две сцепленные переменные обладают следующим свойством: как только одна из них принимает конкретное значение, то же самое конкретное значение принимает и другая.

Если читатель заметил сходство между установлением соответствия и приравниванием аргументов (разд. 2.4), то он совершенно прав. Дело в том, что предикат '=' пытается сделать свои аргументы равными путем установления соответствия между ними.

Попытаемся применить на практике наши знания об операторах, арифметических действиях и установлении соответствия. Предположим, что в базе данных находятся следующие факты:

сумма(5).

сумма(З).

сумма(X+Y).

Рассмотрим вопрос:

?- сумма(2+3).

Какой из вышеприведенных фактов будет соответствовать данному запросу? Если вы думаете, что таковым будет первый факт, вам следует вернуться назад и еще раз прочесть разделы о структурах и операторах. В вопросе аргументом структуры сумма является структура с функтором + и компонентами 2 и 3. На самом деле указанной цели соответствует третий факт, при этом переменные X и Y принимают конкретные значения 2 и 3.

С другой стороны, если программист действительно хочет вычислить сумму, ему следовало бы воспользоваться предикатом is. Он должен был бы написать

?- X is 2+3.

или (в качестве развлечения) он мог бы определить предикат сложить, связывающий два целых числа и их сумму:

сложить (X, Y, Z):- Z is X+Y.

В этом определении X и Y должны быть конкретизированы, а Z неконкретизирована.

ГЛАВА 3. ИСПОЛЬЗОВАНИЕ СТРУКТУР ДАННЫХ

Оксфордский толковый словарь английского языка определяет слово «рекурсия» следующим образом:

РЕКУРСИЯ. [Теперь употребляется редко, устаревшее.] Обратное движение, возвращение.

Это определение загадочно и, по-видимому, устаревшее. В настоящее время рекурсия является очень популярным и мощным средством в области нечислового программирования. Она используется в двух случаях: для описания структур, имеющих другие структуры в качестве компонент, и для описания программ, выполнению которых предшествует выполнение их собственной копии. Иногда начинающие программисты относятся к рекурсии с подозрением, не понимая, как это можно определить некоторое отношение через само себя? В Прологе рекурсия – это нормальный и естественный способ представления структур данных и программ. Мы надеемся, что тема этой главы – рекурсия – обретает ясность удобным и ненавязчивым образом.

Дата добавления: 2014-12-08