Сортировка с помощью дерева

Сортировка

Сортировка

Сортировка

| 44 | 18 | 06 | 42 | 94 | 55 | 12 |~67"

| 06 | 18 | 12 | 42 | 44 | 55 || 94 |~б7

XXAKKKK7

| 06 | 12 I 18 | 42 | 44 | 55 | 67 | эЦ

Рис. 3.5. Пример сортировки Шелла

Приводимая программа не ориентирована на некую определенную последовательность расстояний. Все t расстояний обозначаются соответственно hi, hi,..., h_t, для них выполняются условия:

h_t=\;

h_i+i < h_t.

Каждая /ьсортировка программируется как сортировка с помощью прямого включения.

Анализ алгоритма. При анализе алгоритма возникают очень сложные математические задачи, многие из которых ещё не решены [3, 9]. В частности, не известно, какие расстояния дают наилучшие результаты. Однако выявлен удивительный факт, что они не должны быть множителями друг другу. Дональд Кнут рекомендует такую последовательность [9]:

1 3 7 15 31 где

h_k_x=2h_k+ l;

h_t= 1 и r=[log₂«]-l. В этом случае затраты на сортировку п элементов пропорциональны п '.

Метод сортировки с помощью прямого выбора основан на повторяющихся поисках наименьшего ключа среди п элементов, затем среди п-\ элементов и так далее. Улучшить сортировку можно в том случае, если получать от каждого прохода больше информации, чем просто идентификация единственного элемента [1,3,9,10,13]. Например, с помощью п/2 сравнений можно определить наименьший ключ из каждой пары элементов; при помощи следующих п1А сравнений можно выбрать наименьший из каждой пары уже выбранных наименьших ключей; наконец, при помощи п-\ сравнения можно построить дерево выбора и определить корень как наименьший ключ (рис. 3.6).

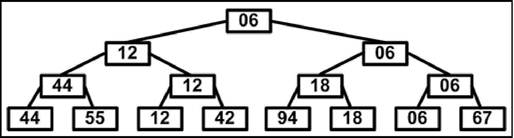
Рис. 3.6. Повторяющиеся наборы среди двух ключей

На втором шаге спускаемся по пути, указанному наименьшим ключом и исключаем его, последовательно заменяя на «дыру», либо на элемент, находящийся на противоположной ветви промежуточного узла (рис. 3.7).

Элемент, оказавшийся в корне дерева, вновь имеет наименьший ключ и может быть исключен. После п шагов дерево становится пустым, и процесс сортировки заканчивается. Каждый из п шагов требует logw сравнений. Поэтому вся сортировка требует n-\og2ⁿ операций, не считая п шагов на построение дерева. Это значительное улучшение по сравнению с прямым методом выбора, который

требует п шагов, но и даже по сравнению с сортировкой Шелла, которая требует п ' шага.

щ [н] QU и и и □ и

ЗАПОЛНЕНИЕ «ДЫРОК»

Дата добавления: 2014-11-29