Пирамидальная сортировка

ВЫБОР НАИМЕНЬШЕГО КЛЮЧА

Рис. 3.7

Наша очередная задача — найти способы эффективной организации информации, обрабатываемой на каждом шаге.

Во-первых, желательно избавиться от необходимости в «дырах»; во-вторых, нужно найти способ представить дерево из п элементов в виде массива.

Метод пирамидальной сортировки, изобретенный Д. Уилльямсом, является улучшением традиционных сортировок с помощью дерева [1, 3, 9, 10, 13]. Пирамидой называется двоичное дерево такое, что

a[i] <a[2*i]; a[f\<a[2*i+ 1]. Отсюда следует, что а[\] — минимальный элемент пирамиды.

Сначала расположим исходный массив в пирамиде, а затем пересортируем элементы. Это и есть общая идея пирамидной сортировки (рис. 3.8).

		а[1]
< а[4]	2] ч а[51		а < а[6]	[3] \ а[7]

Рис. 3.8

Выполнение алгоритма разбивается на два этапа.

I этап. Построение пирамиды. Определяем правую часть дерева, начиная с п/2 + 1 (нижний уровень дерева). Берем элемент левее этой части массива и просеиваем его сквозь пирамиду по пути, где находятся меньшие его элементы, которые одновременно поднимаются вверх; из двух возможных путей выбираете путь через меньший элемент.

Массив для сортировки:

24, 3, 15, 20, 52, 6.

Расположим элементы в виде исходной пирамиды; номер элемента правой части (6/2 + 1) = 4. Просеиваемый элемент имеет номер 3 (рис. 3.9).

3' У	N		У

Рис. 3.9

Результат просеивания элемента 15 через пирамиду показан ниже (рис. 3.10).

		3f		У

Рис. 3.10 155

Следующий просеиваемый элемент 31; затем — 24 (рис. 3.11).

	24*
	^ \		гГ
		f X	N		/

Рис. 3.11

Разумеется, полученный массив еще не упорядочен. Однако, процедура просеивания является основой для пирамидальной сортировки. В итоге просеивания наименьший элемент оказывается на вершине пирамиды. Оформим функцию просеивания элемента с индексом left сквозь часть пирамиды left+\,..., right.

II этап. Сортировка на построенной пирамиде. Берем последний элемент массива в качестве текущего. Меняем первый элемент массива (верхний элемент пирамиды, он наименьший) и текущий местами. Текущий элемент (он теперь первый) просеиваем сквозь п-\ элементную пирамиду. Затем берем предпоследний элемент и т.д.

1. Исходной является построенная ранее пирамида. Меняем местами элементы 6 и 24: элемент 6 встал на место (рис. 3.12).

Просеиваем элемент 24 сквозь пирамиду, не трогая элемента 6. В итоге просеивания на вершине окажется 15 — наименьший элемент из оставшейся части массива.

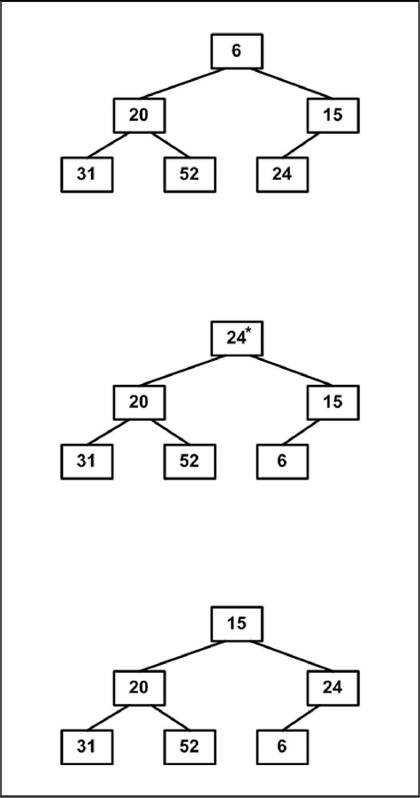
Рис. 3.12

2. Теперь уже два элемента на месте. Продолжим процесс (рис. 3

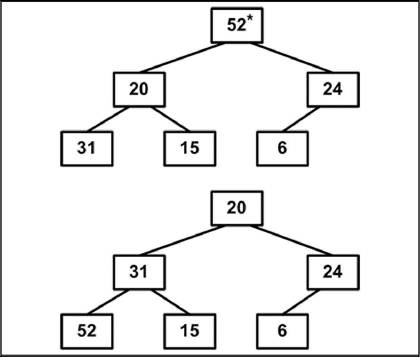
Рис. 3.13

Рис. 3.14

3. Продолжим процесс. В итоге массив будет отсортирован по убыванию (рис. 3.14).

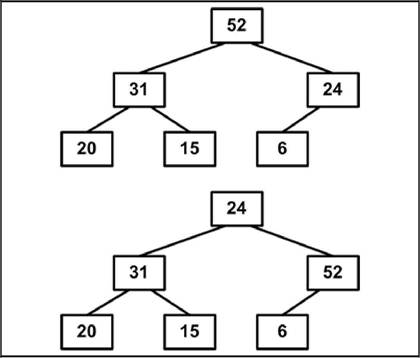
Алгоритм пирамидальной сортировки

void heapSort(int numbers[], int array_size)

{

int i, temp;

for (i = (array_size / 2)-l; i >= 0; i--) siftDown(numbers, i, array_size);

for (i = array_size-l; i >= 1; i--)

{

temp = numbers[0];

numbers[0] = numbers[i];

numbers[i] = temp;

siftDown(numbers, 0, i-1); } }

void siftDown(int numbers[], int root, int bottom)

{

int done, maxChild, temp;

done = 0;

while ((root*2 <= bottom) && (!done))

{

if (root*2 == bottom)

maxChild = root * 2; else if (numbers[root * 2] > numbers[root * 2 + 1\

maxChild = root * 2; else

maxChild = root * 2 + 1;

if (numbers[root] < numbers[maxChild])

{

temp = numbers[root];

numbers[root] = numbers[maxChild];

numbers[maxChild] = temp;

root = maxChild;

} else

done = 1; }

Анализ алгоритма [3]. Несмотря на некоторую внешнюю сложность, пирамидальная сортировка является одной из самых эффективных. Алгоритм сортировки эффективен для больших п. В худшем случае требуется и-log п шагов, сдвигающих элементы. Среднее число перемещений примерно равно (п/2) -log n, и отклонения от этого значения относительно невелики.

Дата добавления: 2014-11-29