ВВЕДЕНИЕ. Цель работы: определение чувствительности термопары и ее градуировка

ГРАДУИРОВКА ТЕРМОЭЛЕМЕНТА И ОПРЕДЕЛЕНИЕ ЕГО ЧУВСТВИТЕЛЬНОСТИ

РАБОТА № 9

Цель работы: определение чувствительности термопары и ее градуировка.

Приборы и принадлежности: термопара константан-медь, гальванометр, чувствительностью порядка 10 мкА/ дел, два латунных сосуда, два термометра, две пробирки с маслом, электроплитка, резисторы.

В замкнутой цепи, состоящей из двух различных проводников (называемой термопарой), возникает электрический ток, если спаи этих проводников имеют разную температуру. Возникновение электрического тока означает, что в цепи возникает электродвижущая сила. Она называется термоэлектродвижущей силой, или сокращенно термоэдс. Закон, связывающий термоэдс с температурами Т₁ и Т₂ спаев термопары, имеет вид:

Å= f(T₂) — f(T₁) (1).

Это явление, открытое в 1821 г., называется явлением Зеебека. В случае линейной зависимости f(T) = f₀ + aT, получаем:

Å = a(T₂ — T₁) (2).

Опыт показывает, что линейное представление возможно только для небольших интервалов температур и далеко не для всех пар металлов.

Существует и обратный термоэлектрический эффект, открытый в 1884 году Ж.Пельтье. При прохождении тока по термопаре возникает разность температур спаев.

Рассмотрим теорию эффекта Зеебека в металлах. Пусть два металла А и В приведены в со­прикосновение друг с другом, причем температура обоих металлов Т=0К. Как известно, в металлах при Т=0К электроны заполняют состояния в зоне проводимости, начиная с со­стояния с нулевой энергией, вплоть до состояний с максимальной энергией, называемой энергией Ферми, которую будем обозначать буквой Е_F. Энергия Ферми зависит от рода металла (в первую очередь энергия Ферми определяется плотностью числа электронов), по­этому Е_FA ¹ Е_FB. Допустим для определенности, что Е_FA < Е_FB, это означает, что в металле В плотность числа электронов выше, чем в металле А. Тогда, если металлы А и В соприкасаются друг с другом то электроны из металла В начнут переходить в металл А на незаполненные уровни зоны проводимости, иными словами возникнет диффузия электронов из В, где их много, в А, где их мало. Поскольку металл В теряет электроны, то он будет приобретать положительный заряд, т.е. потенциал его будет расти, а потенциальная энергия электронов в нем ej_B- понижаться, т.к. заряд электронов e - отрицателен. Металл А будет заряжаться отрицательно из-за притока электронов, а потенциальная энергия электронов в нем ej_А по­вышаться. Итак, полная энергия электронов в металле А будет возрастать, а в металле В - понижаться. Ток в контакте прекратится, когда полная энергия электронов на верхних уровнях зон в обоих металлах станет одинаковой. Это произойдет в том случае, когда:

Е_FA + ej_А = Е_FB +ej_B (3).

Как доказывается в статистической физике, равенство (3) справедливо и при Т¹ 0К. Условие (3) есть условие термодинамического равновесия тела, помещенного в электрическое поле. Как видим, в состоянии равновесия между двумя металлами существует разность потенциалов j_A - j_B = (E_FB-E_FA)/e. Для объяснения явления Зеебека следует иметь в виду два факта:

1. Энергия Ферми Е_F зависит от температуры Т:

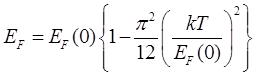(4).

где E_F (0) - значение энергии Ферми при Т=0К.

2. Согласно закону Ома для неоднородного участка цепи разность потенциалов на концах разомкнутой цепи

j₂ —j₁ = E,

где E - эдс, действующая в данном участке. Следовательно, эдс в цепи можно определить, измеряя разность потенциалов на концах разомкнутой цепи.

Рассмотрим теперь термоэлемент, т.е. цепь, образованную двумя различными проводниками А и В. Температуры спаев Т₁ и Т₂ будем считать различными. Чтобы определить эдс в этой цепи, ее надо разорвать и определить разность потенциалов между получившимися концами цепи. Эдс, т.е. разность потенциалов между концами цепи равна разности скачков потенциала в спаях 1 и 2. На основании (3) находим:

e(j₂ – j₁)_конт = [E_FB(T₂) – E_FA(T₂)] – [ E_FB(T₁) – E_FA(T₁)] (5).

Результат, содержащийся в (5) дает не всю термоэдс, а лишь ее часть, так называемую контактную тэдс поскольку она обу­словлена явлениями в контактах двух металлов. С помощью (4) нетрудно убедиться, что при малых разностях температур спаев термоэдс оказывается пропорциональной первой степени разности температур спаев, т.е.

E _конт=a_конт(T₂ – T₁),

где коэффициент a_конт , вообще говоря, зависит от температуры.

Вторая причина возникновения термоэдс состоит в следующем. Представим себе однородный проводящий стержень, концы которого поддерживаются при разных температурах. Поскольку энергия электронов, а, стало быть, и их скорость растут с увеличением температуры, то на горячем конце стержня ско­рость электронов будет выше, чем на холодном конце. Поэтому возникает поток электронов от горячего конца к холодному (это явление носит название термодиффузии), в результате чего горячий конец из-за оттока электронов начнет заряжаться положительно, а холодный из-за притока электронов - отрицательно. Следовательно, в стержне возникнет электрическое поле, направленное от горячего (положительно заряженного) конца стержня к холодному (отрицательно заряженному). Электрическое поле будет замедлять электроны, движущиеся от горячего конца к холодному, и ускорять электроны, движущиеся в обратном направлении. Поэтому рано или поздно потоки горячих и холодных электронов сравняются и заряды на концах стержня изменяться больше не будут. Таким образом, в неравномерно нагретом проводнике в отсутствии электрического тока будет существовать электрическое поле. Поскольку поле возникает благодаря неравномерному нагреву, то ясно, что напряженность поля Е будет функцией градиента температуры, или в случае стержня, функцией dT/dx (ось OХ направлена вдоль оси стержня от горячего конца к холодному):

E=f(dT/dx).

Обычно в проводниках градиенты температуры невелики, поэтому функцию можно разложить в ряд по степеням малого параметра dT/dx:

(6).

В равномерно нагретом (T = const) стержне, очевидно, нет никакого поля, и следовательно, E₀=0. Поскольку вектор Е направлен от горячего конца стержня к холодному, т.е. в сторону убывания температуры, то a<0, поэтому коэффициент при dT/dx можно обозначить через -a (коэффициент a, вообще говоря, зависит от температуры), и тогда

E= — adT/dx.

Вводя потенциал электрического поля j: E= —dj/dx, получаем

dj = a dT.

Для разности потенциалов на концах термоэлемента (см. рис. 1), т.е. его эдс имеем:

E =

Окончательно:

E =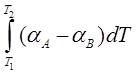

Воспользовавшись теоремой о среднем, получим:

E _дифф = (7).

Общая термоэдс в термопаре будет равна:

E = E _дифф + E _конт =(a_дифф +a_конт)(T₂-T₁)= a(T₂-T₁) (8),

где a - удельная термоэдс.

Учитывая, что a зависит от температуры, нельзя ожидать линейной зависимости термоэдс от разности температур спаев T₂-T₁. Тем не менее, для некоторых интервалов температур можно подобрать такие термопары, которые дают сравнительно хорошую линейную зависимость термоэдс от температуры в диапазоне от O⁰С до 800⁰ С, если один из спаев поддерживать при температуре 0⁰С.

Дата добавления: 2014-11-29