ЗАКОН «ТРЕХ ВТОРЫХ»

Выведем соотношение между током и анодным напряжением предполагая что:

1. сила тока в лампе не зависит от времени,

2. катод и анод являются параллельными плоскостями,

3. скорость электронов, выходящих из катода равна нулю,

4. напряженность электрического поля на поверхности катода равна нулю из-за наличия облака электронов у поверхности катода.

Напряженность электрического поля E и объемная плотность зарядов r, создаваемых электронами, связаны теоремой Гаусса:

div E = 4pr.

Вводя потенциал электрического поля j, и учитывая, что E = – grad j, получим для потенциала уравнение Пуассона:

Dj= – 4pr (1).

Здесь, как обычно, символом Dj обозначена сумма вторых частных производных от j по координатам:

Dj = .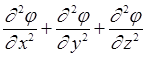

В нашем случае, когда катод и анод представляют собой параллельные плоскости, потенциал изменяется лишь в направлении, перпендикулярном этим плоскостям. Выбрав систему координат с осью OX перпендикулярной катоду, получим, что в (1) производные по y и z обращаются в нуль и (1) приобретает более простой вид:

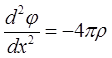(2).

Выберем направление оси OX от катода к аноду, а начало координат на катоде. Пусть расстояние между катодом и анодом равно d. В качестве граничных условий для j примем:

j(0)=0 (условие на катоде) и

j(d)=U_a (условие на аноде).

Кроме того, поскольку напряженность поля на катоде мы приняли равной нулю, то на катоде, т.е. при x=0, dj/dx=0.

Плотность тока связана со скоростью зарядов и их плотностью известным соотношением:

j =r v. (3).

Согласно уравнению непрерывности

,

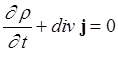и поскольку мы считаем, что ток в лампе не зависит от времени, то и плотность заряда r также будет постоянной. Следовательно, div j =0 и, поскольку все величины в нашем случае зависят лишь от одной координаты x, получаем, что dj/dx=0, т.е. плотность тока не зависит от координат:

j=const (4).

Скорость электронов можно определить из закона сохранения энергии:

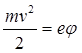(5).

Здесь мы учли, что начальная скорость электронов равна нулю и потенциал на катоде выбран также нулевым. Кроме того, через e мы обозначили абсолютную величину заряда электрона.

Выразив плотность r через j и v из (3), а v через j из (5), получим вместо (2) уравнение:

.

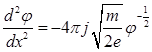Умножив обе стороны уравнения на dj/dx и проинтегрировав по dx, получим:

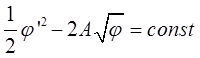(6).

Здесь через A мы обозначили постоянную, равную 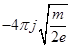. Эта константа положительна, т.к. электроны летят от катода к аноду, т.е. в положительном направлении, а ток течет навстречу движению электронов, следовательно, j<0 и A>0.

Константа в правой части уравнения (6), в силу нулевых граничных условий для j, равна нулю. Тогда из (6) мы получим:

.

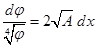Интегрируя это уравнение с учетом значения постоянной A и условий для j при x=0 и x=d, получим:

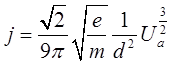(7).

Это и есть закон трех вторых. Мы получили его для случая плоских анода и катода. В случае цилиндрической геометрии электродов подход к решению задачи тот же, но вычисления оказываются значительно сложнее. И в этом случае плотность тока оказывается пропорциональной напряжению в степени три вторых. Мы не будем проводить расчеты для цилиндрической геометрии, и ограничимся рассмотренным плоским случаем.

ПРИЛОЖЕНИЕ 2

Дата добавления: 2014-11-29