Вывод формулы Ричардсона – Дэшмана

Для вывода формулы Ричардсона-Дэшмана найдем количество электронов, вылетающих из катода в единицу времени. Необходимо при этом учитывать, что в металле распределение электронов по энергиям подчиняется закону Ферми-Дирака:

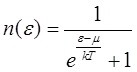(1),

где n(e) есть среднее число электронов с энергией e, m – энергия Ферми. Как видно из (1) при температуре Т=0 все состояния с e<m заняты (n(e)=1), а с e>m – пусты (n(e)=0). Таким образом, m представляет собой максимальную энергию, которой могут обладать электроны в металле при нулевой температуре. В большинстве металлов энергия Ферми имеет порядок 1 эВ[13]. Если T>0, то электроны могут обладать энергиями, превышающими энергию Ферми, однако, как видно из (1), энергия этих электронов отличается от m лишь на величину порядка kT. Поскольку обычно T составляет величину не превышающую 2500К–3000К, то kT<<m. Число же электронов с энергиями, заметно превышающими m, ничтожно мало. Все это иллюстрируется рис. 1, где пунктирной линией изображена функция распределения Ферми-Дирака при T=0, а сплошной – при T>0.

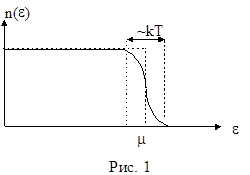
Тот факт, что электроны не могут самопроизвольно выйти из металла, означает, что они удерживаются в нем некоторыми силами. Это можно трактовать так, что электроны металла находятся в потенциальной яме, высота стенок которой достаточно велика для того, чтобы электроны не могли выскочить из нее. Все это можно схематически изобразить в виде графика зависимости потенциальной энергии электрона от его координат. Этот график изображен на рис. 2, где координата х отсчитывается в направлении, перпендикулярном поверхности металла. Металлу соответствуют отрицательные x, вакууму - положительные.

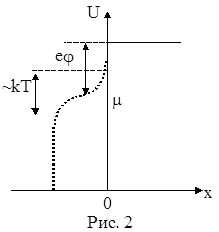
Поскольку наибольшая кинетическая энергия электронов при Т=0 равна энергии Ферми m, то работа, которую необходимо совершить для удаления электрона из металла, равна разности между высотой потенциального барьера и энергией Ферми. Эта величина носит название работы выхода. Ее записывают как e×j, где e‑ величина заряда электрона, а j тогда имеет размерность потенциала. Потенциал j для большинства металлов составляет величину от вольта до нескольких вольт. Здесь же на графике изображена функция распределения Ферми-Дирака, показывающая, как изменяется число электронов с ростом их энергии.

С ростом температуры возрастает количество электронов с высокими энергиями. Те электроны, энергия которых превышает энергию Ферми на величину большую работы выхода, могут выйти из металла. Это и есть термоэлектронная эмиссия.

Таким образом, для нахождения тока термоэлектронной эмиссии необходимо найти поток электронов с достаточно большими энергиями в направлении поверхности металла. Поскольку силы, удерживающие электроны в металле, направлены перпендикулярно его поверхности, то для нахождения тока эмиссии следует найти количество электронов, у которых скорость в направлении поверхности металла v_x такова, что:

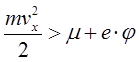(2).

Проекции скорости частицы на направление, параллельное поверхности металла v_x и v_y, могут быть при этом любыми.

Движение электронов в металле подчиняется законам квантовой механики, согласно которым всякая частица обладает также и волновыми свойствами. Длина волны l (волна Де Бройля), которой обладает частица, равна, как известно:

l=2p‚/p,

где p - импульс частицы, ‚- постоянная Планка. Поскольку электроны в металле находятся в стационарном состоянии, то это означает, что длины волн электронов могут иметь лишь некоторые определенные значения. Все это приводит к тому, что в единице объема количество электронов с заданным значением импульса p оказывается равным:

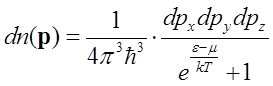(3).

Здесь dp_x, dp_y, dp_z – значения интервалов, в пределах которых заданы значения проекций импульса. Энергия электрона e= 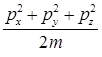, где m – его масса.

Если (3) проинтегрировать при T=0 по dp_x, dp_y, dp_z в пределах от –¥ до +¥, то мы получим соотношение между концентрацией электронов в металле n и энергией Ферми m:

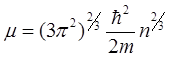(4).

При T>0 значение m мало отличается от (4).

Найдем теперь плотность тока термоэлектронной эмиссии. Для этого запишем количество электронов, имеющих проекции импульса p_x, p_y, p_z и достигающих площадки площади dS на поверхности металла за некоторое малое время dt:

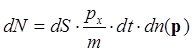(5).

Для нахождения тока необходимо умножить dN на заряд электрона e. Как уже было отмечено, выходят за пределы поверхности металла лишь те электроны, у которых 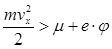, или p_x>p₀, где:

p₀= .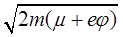

Интегрируя (5) по dp_x в пределах от p₀ до бесконечности, а по dp_y и dp_z от минус до плюс бесконечности, получим плотность тока эмиссии:

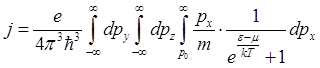(6).

Вычисление (6) нетрудно произвести в случае, когда ej>>kT, что обычно имеет место в реальных условиях работы катода. В этом случае показатель экспоненты оказывается большим и единицей по сравнению с экспонентой можно пренебречь. Тогда интеграл превращается в значительно более простой:

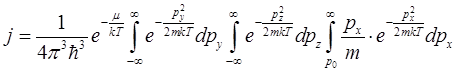(7).

Интегрирование по dp_x выполняется элементарно, если сделать замену переменных , после чего получаем:

.

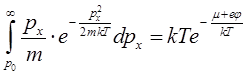Интегралы по dp_y и dp_z одинаковы и представляют собой известный интеграл Пуассона:

,

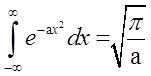в котором a =1/2mkT.

Таким образом, находим плотность тока эмиссии:

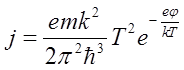(8).

Полученный результат (8) представляет собой известную формулу Ричардсона – Дэшмана, в которой множитель, стоящий перед T² имеет величину 120,4 ампер/см²×град², что заметно больше тех величин, которые обычно наблюдаются в экспериментах с термоэлектронной эмиссией с поверхности чистых металлов. Это расхождение объясняется тем, что часть электронов отражается от поверхности металла. В соответствии с этим необходимо умножить плотность тока в (8) на множитель 1-r, где r - коэффициент отражения электронов от поверхности металла. Что касается вычислений значения коэффициента r, то никаких надежных способов такого вычисления нет, поскольку результат определяется индивидуальными свойствами поверхности. Итак, с учетом возможного отражения электронов от поверхности металла получаем:

.

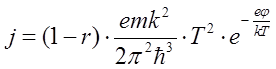ЛИТЕРАТУРА

1. И.В. Савельев. Курс общей физики. Т.3. М. Наука, 1978 и др. издания.

2. И.Е. Иродов. Квантовая физика. М. Физматлит, 2001.

3. И.Е. Иродов. Физика макросистем. М. Физматлит, 2001.

4. Д.В. Сивухин. Общий курс физики, т.т. 4 и 5. М. Наука, 1980.

[1] В качестве приемника излучения используется термопара, один из спаев которой зачернен. Этот зачерненный спай, поглощая падающее на него излучение, нагревается. Подобного рода устройства называются болометрами.

[2] Здесь испускательная способность относится уже к интервалу длин волн dl.

[3] Здесь и дальше все величины, относящиеся к АЧТ, будем помечать звездочкой.

[4] Где С₁=2phc²=3,74×10^-16 Вт/м²,

[5] Оптические пирометры проградуированы по абсолютно черному телу и на шкале нанесены значения яркостных температур.

[6] Строго говоря, в формулу (4) входит приведенная масса электрона:

m=m_e M/(m_e +M),

где М - масса ядра атома водорода, т.е. масса протона, а m_e - масса электрона.

[7] Это является прямым следствием теоремы Гаусса

[8] Более подробно о тонкой структуре см. Приложение

[9] Правила (8) справедливы для переходов между состояниями с различным электрическим дипольным моментом атома, но возможны переходы с изменением магнитного момента или квадрупольных электрических моментов атома. Эти переходы имеют малую вероятность, и в них правила отбора отличаются от (8).

[10] Напомним, что по определению DN

[11] Строго говоря, числоN_эф, выбирается так, чтобы равенство (2) давало правильное число электронов при подстановке энергии дна зоны Е_с вместо энергии Е.

[12] Фактически рост напряжения и в этом случае будет приводить к очень медленному росту тока из катода. Этот, так наз. эффект Шоттки, объясняется понижением работы выхода электронов из катода с ростом внешнего поля.

[13] Напомним, что тепловой энергией равной 1 эВ частицы обладают при температуре 11640 К.

Дата добавления: 2014-11-29