
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Высшая математика
|
|
|
|
Двойные и тройные интегралы
Контрольные задания для студентов – заочников
второго курса всех специальностей
Контрольная работа № 5
Н. Новгород
1999 г.
I ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ
I.I. ДВОЙНОЙ ИНТЕГРАЛ
I. Определение двойного интеграла
Пусть даны: 1) область Д на плоскости х, у;
2) функция двух переменных Z = f (х,у).
Выполним следующее вычисление:
1) разобьем область Д на произвольное число частей произвольных размеров и формы;
2) в каждой части выберем произвольную точку;
3) в каждой из этих точек вычислим значение данной функции;
4) умножим каждое их этих значений на площадь соответствующей части;
5) все такие произведения сложим.
Получившееся число называется ИНТЕГРАЛЬНОЙ СУММОЙ функции f (х,у) в области Д.
Он обозначается
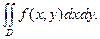
2. Вычисление двойного интеграла
Пусть область Д. ограничена снизу графиком функции у=у1(х), а сверху графиком функции у=у2(х).
Для вычисления двойного интеграла
1) спроектируем область Д. на ось х;
Проекцией будет некоторый промежуток [а,в] на этой оси:
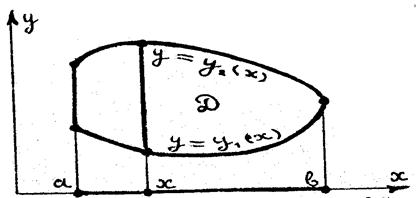
2) зафиксируем на промежутке [а,в] произвольную точку х и приведем через нее вертикальную прямую. Будем передвигаться по ней в направлении возрастания у: при этом f будет функцией Толькой одной переменной у.
Вычислим интеграл этой функции вдоль участка вертикальной прямой, расположенного в области Д.,
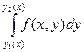 ;
;
3) величина этого интеграла зависит от того, какое взято х, т.е. является функцией от х. Найдем ее интеграл по промежутку а ≤ х ≤ в. Можно доказать, что получившееся число равно искомому двойному интегралу
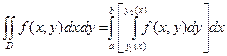
3. Моменты инерции пластинки
Пусть дана однородная материальная пластинка Д.. Поверхностную плоскость (массу, приходящуюся на единицу площади) обозначим ρ.
Найдем J0 - момент инерции пластинки относительно начала координат:
1) разобьем пластинку Д. на какое-либо число n достаточно мелких частей произвольной формы. Их площади обозначим ∆ Sк (к=1,2,…, n);
2) найдем массы отдельных частей ρ · ∆Sк;
3) в каждой части выберем произвольную точку (хк, ук);
4) приближенно найдем момент инерции каждой части, считая ее массу сосредоточенной в точке (хк, ук)
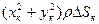 ;
;
5) момент инерции всей пластинки будет
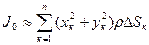 ;
;
6) это равенство тем точнее, чем мельче отдельные части. Следовательно, точное равенство получим, перейдя к пределу при стремлении размеров отдельных частей к нулю, а их числа к бесконечности
 :
:
7) здесь под знаком предела стоит интегральная сумма функции 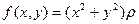 в области Д.. Следовательно, сам предел есть интеграл этой функции по области Д.
в области Д.. Следовательно, сам предел есть интеграл этой функции по области Д.
 .
.
Рассуждение, с помощью которого получена эта формула, типично. Сходным образом, как двойные интегралы, вычисляются и многие другие физические величины, связанные с пластинкой. В частности, так получаются формулы для моментов инерции относительно осей и для площади пластинки, приведенные ниже.
Моменты инерции пластинки Д. относительно начала координат J0, оси абсцисс Jх, оси ординат Jу равны (поверхностная плотность ρ, как постоянная вынесена за знак интеграла)
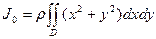 ;
;  ;
; 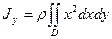 .
.
4. Площадь
Площадь S пластинки Д равна
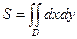 .
.
1.2. ТРОЙНОЙ ИНТЕГРАЛ
5. Определение тройного интеграла
Пусть даны:
1) область W в трехмерном пространстве х, у, z;
2) функция трех переменных u = f(x,y,z);
Выполним следующее вычисление:
1) разобьем область W на произвольное число частей произвольных размеров и формы;
2) в каждой части выберем произвольную точку;
3) в каждой из этих точек вычислим значение данной функции;
4) умножим каждое их этих значений на объем соответствующей части;
5) все такие произведения сложим.
Получившееся число называется ИНТЕГРАЛЬНОЙ СУММОЙ функции f(x,y,z) в области W.
Предел интегрально суммы, когда размеры всех частей стремятся к нулю, а их число к бесконечности, называется ТРОЙНЫМ ИНТЕГРАЛОМ функции f(x,y,z) по области W.
Он обозначается 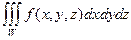 .
.
6. Вычисление тройного интеграла
Пусть область W ограничена снизу графиком функции z=z1(x,y), а сверху графиком функции z=z2(x,y).
Для вычисления тройного интеграла
1) спроектируем область W на плоскость х, у. Проекцией будет некоторая область Д на этой плоскости;

2) зафиксируем в области Д. произвольную точку (х, у) и проведем через нее вертикальную прямую. Будем передвигаться по ней в направлении возрастания z; при этом f будет функцией только одной переменной z. Вычислим интеграл этой функции вдоль участка вертикальной прямой, расположенного в области W.
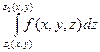 ;
;
3) величина этого интеграла зависит от того, какая взята точка (х,у), т.е. является функцией двух переменных х и у. Найдем ее интеграл по области Д. Можно доказать, что получившееся число равно искомому тройному интегралу
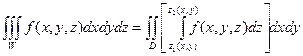
7. Моменты инерции тела
Подобно тому, как физические величины, связанные с пластинкой, вычисляются как двойные интегралы, те же величины, связанные с пространственным телом, вычисляются как тройные интегралы.
Например, вывод формулы для момента инерции J0 тела относительно начала координат делается точно также, как и соответствующей формулы для пластинки (пункт 3) с заменой площадей частичных областей на объемы.
Моменты инерции однородного тела W относительно начала координат J0, оси абсцисс Jх, оси ординат Jy и оси аппликат Jz равны
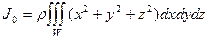 ,
, 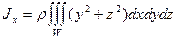
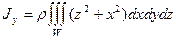 ,
, 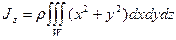
Здесь ρ - объемная плотность.
8. Объем
Объем V тела W равен
V = 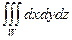
1.3. ТЕОРИЯ ПОЛЯ
9. Поток. Определение
Если в каждой точке (х, у, z) некоторой пространственной области задан вектор, то говорят, что в этой области задано векторное поле. Например, поле скоростей текущей жидкости, поле векторов напряженности электрического заряда.
Пусть заданы:
1) векторное поле 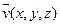 ;
;
2) кусок 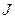 некоторой поверхности;
некоторой поверхности;
3) направление вектора единичной нормали 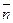 к куску
к куску 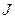 (направление нормали можно задать двумя способами. Например, если
(направление нормали можно задать двумя способами. Например, если 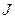 - часть сферы, то нормаль может смотреть стрелкой в центр сферы, а может - в противоположном направлении).
- часть сферы, то нормаль может смотреть стрелкой в центр сферы, а может - в противоположном направлении).
Выполним следующее вычисление:
1) разобьем кусок 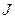 на произвольное число N частей произвольных размеров и формы;
на произвольное число N частей произвольных размеров и формы;
2) в каждой части выберем произвольную точку (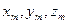 );
); 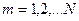 ;
;
3) для каждой из этих точек найдем соответствующий вектор поля 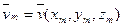 и вектор единичной нормали
и вектор единичной нормали 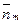 ;
;
4) вычислим скалярные произведения 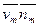 ;
;
5) умножим каждое из этих произведений на площадь ∆Sm соответствующей частичной области. Получатся числа  ;
;
6) сложив все эти числа, получим сумму  ;
;
Предел этой суммы, когда размеры частичных областей стремятся к нулю, а их число к бесконечности называется ПОТОКОМ векторного поля 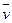 через кусок поверхности J в направлении нормали
через кусок поверхности J в направлении нормали 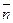 .
.
Он обозначается 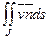 .
.
10. Гидромеханический смысл потока
Если 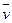 - поле скоростей текущей несжимаемой жидкости, то поток есть выраженное в единицах объема количество жидкости, протекающей в единицу времени через кусок поверхности J в направлении нормали
- поле скоростей текущей несжимаемой жидкости, то поток есть выраженное в единицах объема количество жидкости, протекающей в единицу времени через кусок поверхности J в направлении нормали 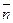 . При этом количество жидкости, протекающее через те части куска J, где угол между векторами
. При этом количество жидкости, протекающее через те части куска J, где угол между векторами 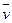 и
и 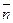 острый, берется со знаком плюс, а через части, где этот угол тупой, - со знаком минус.
острый, берется со знаком плюс, а через части, где этот угол тупой, - со знаком минус.
11. Вычисление потока
Пусть кусок J есть некоторая часть графика функции 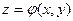 . Тогда вычисление потока сводится к вычислению двойного интеграла по формуле
. Тогда вычисление потока сводится к вычислению двойного интеграла по формуле
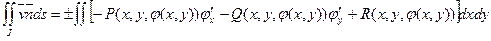 ,
,
где Д есть проекция куска J на плоскость х, у. Знак плюс перед двойным интегралом берется тогда, когда нормаль 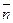 направлена вверх, минус - когда вниз.
направлена вверх, минус - когда вниз.
12. Дивергенция
ДИВЕРГЕНЦИЕЙ векторного поля 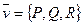 называется скалярная величина, обозначаемая
называется скалярная величина, обозначаемая 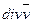 и равна
и равна 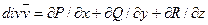 .
.
Гидромеханический смысл дивергенции:
Пусть 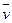 есть поле скоростей текущей сжимаемой жидкости. Кроме того, что такая жидкость движется, она сжимается или растягивается. Если в какой-то точке дивергенция отрицательна, то вблизи этой точки имеет место объемное сжатие, если положительна - растяжение. Абсолютная величина дивергенции служит мерой растяжения - сжатия жидкости вблизи этой точки.
есть поле скоростей текущей сжимаемой жидкости. Кроме того, что такая жидкость движется, она сжимается или растягивается. Если в какой-то точке дивергенция отрицательна, то вблизи этой точки имеет место объемное сжатие, если положительна - растяжение. Абсолютная величина дивергенции служит мерой растяжения - сжатия жидкости вблизи этой точки.
13. Формула Остроградсткого
Нормаль к замкнутой поверхности может быть «внешней», если она направлена изнутри вовне, или «внутренней», если она направлена внутрь области, ограниченной поверхностью.
Поток поля 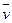 через замкнутую поверхность
через замкнутую поверхность 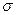 в направлении внешней нормали
в направлении внешней нормали 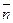 можно вычислить по формуле Остроградского
можно вычислить по формуле Остроградского
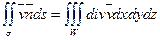 .
.
где W - область, ограниченная поверхность 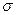 .
.
14. Линейный интеграл. Определение
Дугу (кусок линии), на которой выбрано одно из двух возможных направлений, назовем направленной. Будем ее обозначать двумя буквами: первая - начало дуги, вторая - конец. Так что, если говорим о дуге АВ, то это означает, что на ней выбрано направление от А к В.
Пусть задано векторное поле
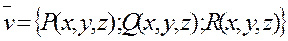 и направленная дуга АВ.
и направленная дуга АВ.
Выполним следующее вычисление:
1) разобьем дугу на произвольное число N частей произвольной длины:
2) вместе с каждой частичной дугой рассмотрим вектор
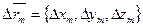 ;
; 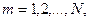
Начало которого совпадает с начальной точкой дуги, а конец - с конечной;
3) на каждой частичной дуге выберем произвольную точку (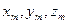 );
);
4) для каждой из этих точек найдем соответствующий вектор поля
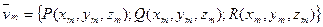 .
.
5) составим скалярные произведения
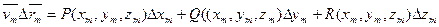 ;
;
6) найдем сумму этих произведений
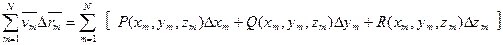 ;
;
7) предел этой суммы, когда длины частичных дуг стремятся к нулю, а их число к бесконечности, называется ЛИНЕЙНЫМ ИНТЕГРАЛОМ векторного поля 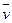 вдоль направленной дуги АВ (или вдоль пути АВ). Он обозначается
вдоль направленной дуги АВ (или вдоль пути АВ). Он обозначается  , или
, или
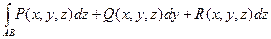 .
.
15. Вычисление линейного интеграла
Пусть дуга АВ есть кусок линии, заданной параметрическими уравнениями 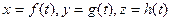 , причем точка А получается при
, причем точка А получается при 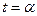 , а точка В - при
, а точка В - при 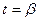 . Тогда вычисление линейного интеграла сводится к вычислению определенного интеграла в соответствии с формулой
. Тогда вычисление линейного интеграла сводится к вычислению определенного интеграла в соответствии с формулой
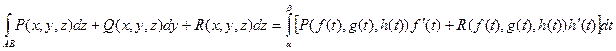 .
.
16. Механический смысл линейного интеграла
Если 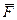 - поле сил, то линейный интеграл
- поле сил, то линейный интеграл 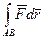 есть работа, совершаемая силой
есть работа, совершаемая силой 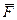 при перемещении материальной точки из положения А в положение В по дуге АВ.
при перемещении материальной точки из положения А в положение В по дуге АВ.
17. Ротор
РОТОРОМ векторного поля 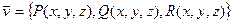 называется вектор, обозначаемый
называется вектор, обозначаемый 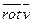 =
= 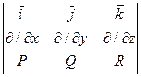
При вычислении определителя умножение символа частной производной (например, 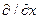 ) на функцию (например, Q) понимают как вычисление соответствующей частной производной (
) на функцию (например, Q) понимают как вычисление соответствующей частной производной (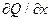 ).
).
18. Гидромеханический смысл ротора
Пусть 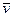 - поле скоростей текущей жидкости. Тогда
- поле скоростей текущей жидкости. Тогда 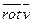 , найденный для какой-нибудь точки, характеризует вращение жидкости вблизи этой точки. Именно:
, найденный для какой-нибудь точки, характеризует вращение жидкости вблизи этой точки. Именно:
1) прямая, на которой расположен ротор, будет осью, вокруг которой вращение происходит наиболее интенсивно;
2) глядя от конца ротора, увидим вращение жидкости, происходящим против часовй стрелки;
3) длина ротора является мерой интенсивности вращения жидкости.
19. Формула Стокса
Линейный интеграл вдоль замкнутого контура λ называется ЦИРКУЛЯЦИЕЙ и обозначается 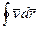 . Выбранное направление указывается дополнительно.
. Выбранное направление указывается дополнительно.
Циркуляцию можно вычислить по формуле Стокса

Здесь ζ - кусок любой поверхности, ограниченный контуром λ. Единичная нормаль  к этому куску выбирается так, чтобы, глядя с ее конце, видеть движение по контуру в выбранном направлении, происходящим против часовой стрелки.
к этому куску выбирается так, чтобы, глядя с ее конце, видеть движение по контуру в выбранном направлении, происходящим против часовой стрелки.
Словами эта формула читается так: циркуляция векторного поля вдоль какого-либо контура равна потоку ротора через любую поверхность, натянутую на контур.
20. Потенциальное поле
Векторное поле на плоскости 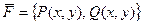 называется ПОТЕНЦИАЛЬНЫМ, если существует такая функция
называется ПОТЕНЦИАЛЬНЫМ, если существует такая функция 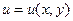 , что
, что  . При этом
. При этом 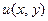 называется ПОТЕНЦИАЛЬНОЙ ФУНКЦИЕЙ поля
называется ПОТЕНЦИАЛЬНОЙ ФУНКЦИЕЙ поля 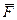 .
.
Теорема (признак потенциальности).
Если 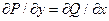 , то поле
, то поле 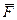 потенциально.
потенциально.
21. Линейный интеграл в потенциальном поле
Линейный интеграл  в общем случае зависит как от положения точек А и В, так и от формы соединяющего их пути.
в общем случае зависит как от положения точек А и В, так и от формы соединяющего их пути.
Теорема. В потенциальном поле линейный интеграл не зависит от формы пути.
Вследствие этого линейный интеграл в потенциальном поле обозначается 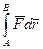 или
или 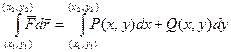
(с указанием начальной и конечной точек пути интегрирования или их координат, без указания самого пути, который выбирается произвольно).
22. Отыскание потенциальной функции
Пусть поле 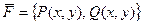 потенциально.
потенциально.
Его потенциальную функцию можно найти по формуле
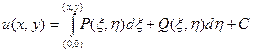
где С - произвольная постоянная.
23. Формула Ньютона-Лейбница для линейного интеграла
Если известна потенциальная функция 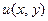 , то линейный интеграл в потенциальном поле
, то линейный интеграл в потенциальном поле 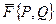 можно вычислить по формуле Ньютона-Лейбница
можно вычислить по формуле Ньютона-Лейбница  ,
,
т.е. линейный интеграл в потенциальном поле равен разности значений потенциальной функции в конечной и начальной точках пути интегрирования.
24. Механический смысл формулы Ньютона-Лейбница
Если 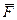 - потенциальное силовое поле, то значение потенциальной функции в какой-либо точке, взятое с противоположным знаком, называют потенциалом поля в этой точке.
- потенциальное силовое поле, то значение потенциальной функции в какой-либо точке, взятое с противоположным знаком, называют потенциалом поля в этой точке.
В соответствии с механическим смыслом линейного интеграла (пункт 16) формула Ньютона-Лейбница истолковывается следующим образом:
Работа, совершаемая силами потенциального поля при перемещении материальной точки по некоторому пути, равна разности потенциалов в начальной и конечной точках пути и не зависит от формы пути.
II. ОБРАЗЕЦ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
1. Вычислить двойной интеграл 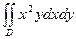 , где область D ограничена линиями х=0, у=х, у=4-х. Изобразить область D.
, где область D ограничена линиями х=0, у=х, у=4-х. Изобразить область D.
 РЕШЕНИЕ. Используя формулу вычисления двойного интеграла
РЕШЕНИЕ. Используя формулу вычисления двойного интеграла 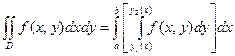 .
.
получим
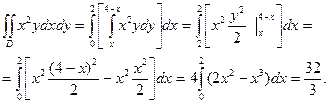
2. Используя тройной интеграл, найти объем тела W, расположенного в первом октанте и ограниченного поверхностями z = 1- х/2 и у= 1 – х2 совместно с координатными плоскостями. Изобразить тело W и его проекцию D на плоскость х, у.
РЕШЕНИЕ.
Уравнение z = 1- х/2 на плоскости z, х определяет прямую линию, а в пространстве - плоскость, проходящую через эту линию и параллельную оси у.
Уравнение у= 1 – х2 на плоскости х, у определяет параболу, а в пространстве - цилиндрическую поверхность - цилиндрическую поверхность, проходящую через эту параболу и параллельную оси z.
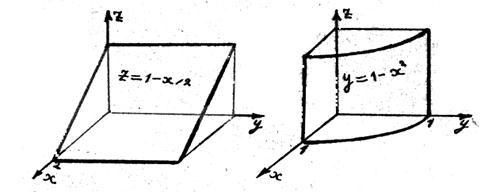
Оставив от цилиндрической поверхности лишь часть, расположенную под плоскостью, изобразим тело W.
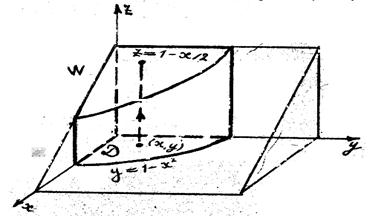
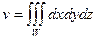
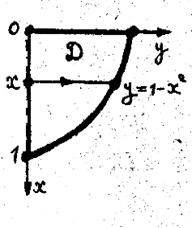 Используя формулу вычисления тройного интеграла
Используя формулу вычисления тройного интеграла
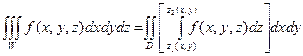 ,
,
получим
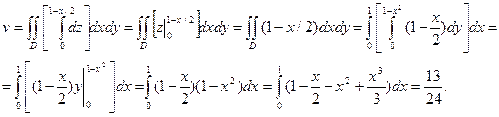
3. Дано: 1) вертикальное поле 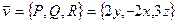 ;
;
2) плоскости 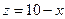 (р) и у= 12 (q), совместно с координатными плоскостями ограничивающие тело W.
(р) и у= 12 (q), совместно с координатными плоскостями ограничивающие тело W.
Для поля 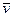 найти:
найти:
1) поток через кусок 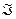 поверхности тела W, принадлежащий плоскости р в направлении внешней нормали
поверхности тела W, принадлежащий плоскости р в направлении внешней нормали  ;
;
2) поток через полную поверхность σ тела W в направлении внешней нормали (использовать формулу Остроградского);
3) линейный интеграл вдоль ребра АВ тела W, расположенного на линии пересечения плоскостей р и q. Ребро проходится в направлении убывания координаты х;
4) циркуляцию вдоль контура λ, ограничивающего кусок 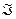 . Конур обходится против часовой стрелки, если смотреть сверху. (использовать формулу Стокса).
. Конур обходится против часовой стрелки, если смотреть сверху. (использовать формулу Стокса).
Сделать рисунок.
РЕШЕНИЕ.
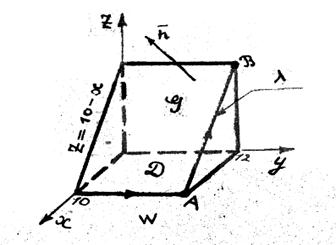
1) 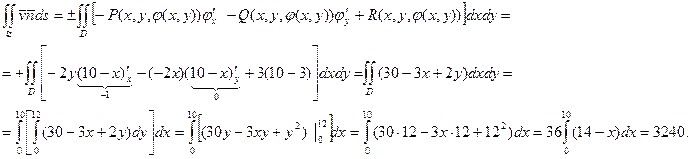
2) 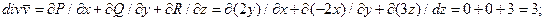
По формуле Остроградского
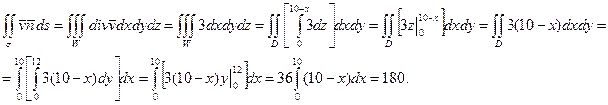
3) общие уравнения прямой АВ будут 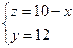
Положим х = t и получим параметрические уравнения х = t, y=12, z = 10 – t.
Тогда А получается при t = 10, точка В - при t = 0.
В соответствии с формулой вычисления линейного интеграла
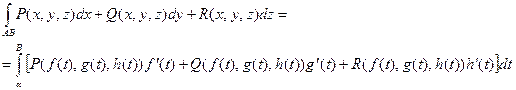
имеем
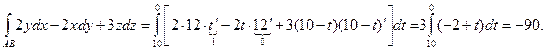
4) 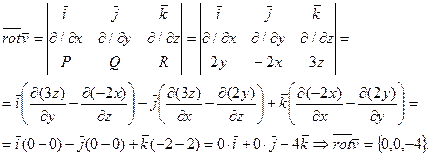
Применим формулу Стокса, взяв кусок 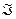 в качестве поверхности, натянутой на контур λ.
в качестве поверхности, натянутой на контур λ.
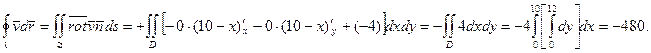
4. Дано векторное поле 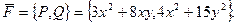
Нужно:
1) убедиться, что потенциально;
2) найти потенциальную функцию 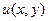 (используя линейный интеграл);
(используя линейный интеграл);
3) сделать проверку;
4) используя потенциальную функцию, найти линейный интеграл 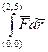 .
.
РЕШЕНИЕ:
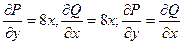
Следовательно, поле потенциально.
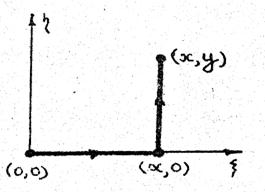 2)
2) 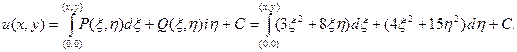
В качестве пути интегрирования возьмем изображенную на рисунке ломаную линию
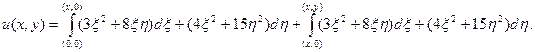
Параметрические уравнения горизонтального участка будут 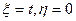 , причем точка (0,0) получается при t = 0, а точка (х,0) при t = x.
, причем точка (0,0) получается при t = 0, а точка (х,0) при t = x.

Параметрические уравнения вертикального участка будут  , причем точка (х,0) получается при t = 0, а точка (х, у) при t = y.
, причем точка (х,0) получается при t = 0, а точка (х, у) при t = y.
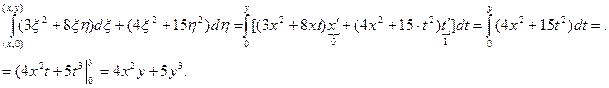
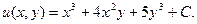
3) проверка
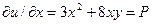 ,
, 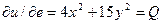 .
.
4) 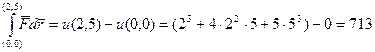 .
.
III. ЗАДАНИЕ КОНТРОЛЬНОЙ РАБОТЫ № 5.
2. Используя тройной или двойной интеграл, найти объем тела W, расположенного в первом октанте и ограниченного указанными поверхностями совместно с плоскостями координат.
| 2.00 Ζ = 2-х, у=1-х2/4 | 2.13 Ζ = 1-у2, у=1-х2 |
| 2.01 Ζ = 1-х. у=1-х2 | 2.14 Ζ = 2-х2 / 2, у=1-х |
| 2.02 Ζ = 1-у, у=1-х2 | 2.15 Ζ = 1-х2 / 4, у = 1-х2 |
| 2.03 Ζ = 1-х2, у=1-х2 | 2.16 Ζ = 1-х2, у=1-х2 / 4 |
| 2.04 Ζ = 1-х2, у=1-х | 2.17 Ζ = 1-х3 / 4, у=1-х |
| 2.05 Ζ = 1-х2/4, у= 1- х2/4 | 2.18 Ζ = 1-х2, у=1-х/2 |
| 2.06 Ζ = 1-х2. у= (1-х2)/2 | 2.19 Ζ = 1-у/2, у=1-х2 |
| 2.07 Ζ = 1-х2/4, у=1-х/2 | 2.20 Ζ = 2-у2/2, у=1-х/2 |
| 2.08 Ζ = 1-у, у=1-х2 / 4 | 2.21 Ζ = 2-у2/2, у=1-х2/4 |
2.09 Ζ = 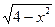 , у= , у= 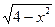
| 2.22 Ζ = 1-х, у= 1-х2/4 |
| 2.10 Ζ = 1-у2, у=1-х2/4 | 2.23 Ζ = 1-у2, у=(1-х2)/2 |
| 2.11 Ζ = 1-х2/4, у=(1-х2)/2 | 2.24 Ζ = 1-у2, у=(1-х)/2 |
2.12 Ζ = 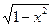 , у = , у = 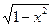
|
Студент выполняет работу по варианту, номер которого равен остатку от деления его шифра на 25. Например, если шифр оканчивается на 82, то номер варианта 07.
Литература
Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. – М.: Наука, 1970. – т.2.
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 828; Нарушение авторских прав?; Мы поможем в написании вашей работы!