Загальні відомості про коливальні процеси.2. Гармонічні коливання. Рівняння гармонічного коливання гармонічних коливань

Тема 7. Електромагнітні коливання і хвилі.

Коливанням називається всякий рух або зміна стану тіла, що характеризується тим чи іншим ступенем повторюваності в часі значень фізичних величин, які визначають цей рух або стан тіла.

Коливання називаються періодичними, якщо значення фізичних величин, які змінюються в процесі коливань, повторюються через однакові проміжки часу. Найпростішим типом періодичних коливань є так звані гармонічні коливання – коливання, при яких значення фізичної величини змінюється з часом за законом косинуса (синуса).

Коливання називаються вільними або власними, якщо вони здійснюються за рахунок енергії, яка була надана, за відсут­ності в наступному зовнішніх періодичних впливів на коливну систему.

Нехай матеріальна точка здійснює вільні гармонічні коливання вздовж осі координат 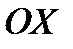біля положення рівноваги, яке прийняте за початок координат. Тоді залежність координати х від часу задається рівнянням

.

тут x – зміщення коливної точки; 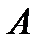– амплітуда коливання ; – власна циклічна частота; – початкова фаза коливань в момент часу 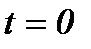; 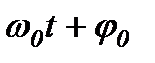– фаза коливань в момент часу t.

Найменший проміжок часу Т, після проходження якого повторюються значен­ня всіх фізичних величин, що характери­зують коливання, називається періодом коливання. За час Т здійснюється одне
повне коливання і фаза коливань отримує приріст 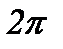, тобто

.

Звідси

.

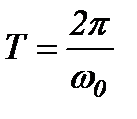Частотою коливань називається кількість повних коливань, що здійсню­ються за одиницю часу:

,

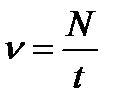де N – кількість коливань, виконаних за час t. Частота коливань – величина, яка обернена до періоду коливань:

.

Циклічна частота

.

Отже, циклічна частота дорівнює кількості повних коливань, що здійснюєть­ся за 2p с.

Коливальний процес характеризується швидкістю і прискоренням коливної точки:

,

,

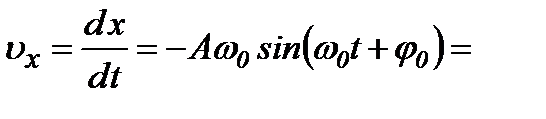
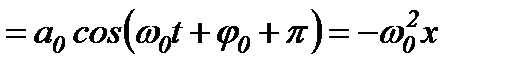де – амплітуда швидкості, – амплітуда прискорення. Зміщення, швидкість і прискорення точки, що гармонічно коливається, є періодичними функціями часу з однаковими циклічною частотою 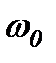і періодом Т. Фаза швидкості відрізняється від фази зміщення на , а фаза прискорення відрізняється від фази зміщення на (рис. 23).

В моменти часу, коли , швидкість 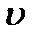набуває найбільшого значення, коли ж досягає максимального від’єм­ного значення, то прискорення 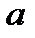набуває найбільше додатне значення.

Прискорення завжди напрямлене до положення рівноваги: віддаляючись від положення рівноваги, коливна точка руха­ється сповільнено, наближаючись до нього – прискорено. Прискорення прямо пропор­ційне до зміщення, а його напрямок проти­лежний до напрямку зміщення.

Другий закон Ньютона дає змогу в загальному вигляді записати зв’язок між силою і прискоренням для вільних гармонічних коливань матеріальної точки з масою :

.

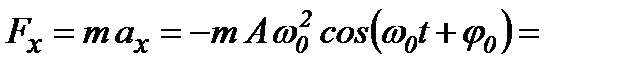
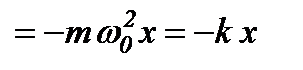Сила, що діє на коливну матеріальну точку прямо пропорційна до зміщення і завжди напрямлена до положення рівноваги. Тому її називають повертальною силою. Фаза сили 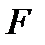збігається з фазою прискорення.

Прикладом сил, що задовольняють співвідношення 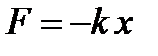, є пружні сили. Сили , що мають іншу природу, ніж пружні сили, але також задовольняють умову 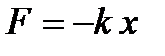, називаються квазіпружними, а 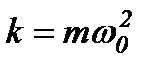– коефіцієнтом квазі­пружної сили.

Для вільних гармонічних коливань вздовж осі OX прискорення 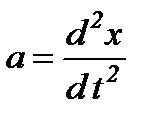. Тоді

,

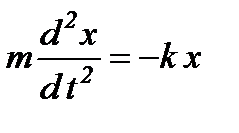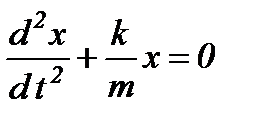
і

,

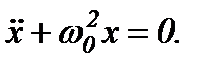
Це диференціальне рівняння вільних гармонічних коливань, збуджених пружними або квазіпружними силами.

Загальними розв’язками цього диференціального рівняння є функції:

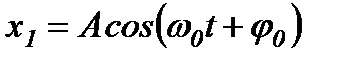або .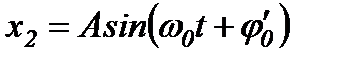

Кінетична енергія матеріальної точки, що здійснює гармонічні коливання, дорівнює:

.

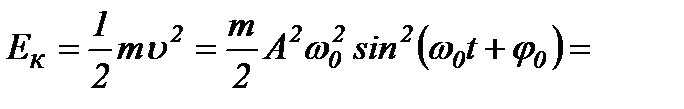
Потенціальна енергія матеріальної точки, що здійснює гармонічні коливання під дією квазіпружної сили, дорівнює:

.

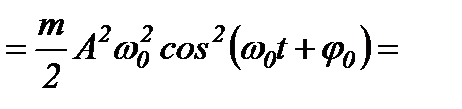
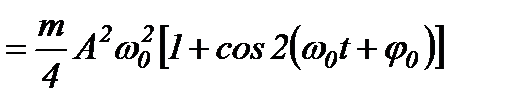Кінетична і потенціальна енергії здійснюють гармонічні коливання з цик­лічною частотою і амплітудою 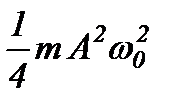біля середнього значення .

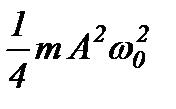Повна механічна енергія коливної точки:

.

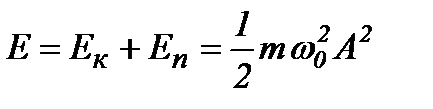Графіки залежностей 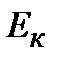, 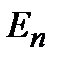і від часу 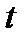для випадку 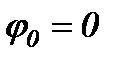наведено на рис. 24.

Квазіпружна сила є консерватив­ною. Тому повна енергія гармонічного ко­ливання залишається сталою. У процесі коливання відбувається перетворення кіне­тичної енергії в потенціальну і навпаки. В момент найбільшого відхилення точки від положення рівноваги повна енергія склада­ється лише з потенціальної енергії. При проходженні точки через положення рів­новаги повна енергія складається лише з кінетичної енергії, яка в цей момент є мак­симальною.

Дата добавления: 2014-11-29