Обоснование метода. В данной работе определение динамической вязкости (коэффициента внутреннего трения) жидкости производится по методу Стокса. Рис

В данной работе определение динамической вязкости (коэффициента внутреннего трения) жидкости производится по методу Стокса.

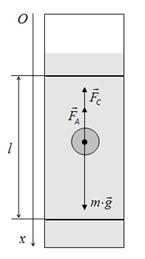
Рис. 2. Движение шарика в жидкости

Пусть некоторое тело шарообразной формы и малых размеров движется в вязкой жидкости вертикально вниз (рис. 2). При этом на него будут действовать три силы: сила тяжести 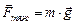, сила Архимеда и сила внутреннего трения жидкости (сила Стокса), направленная в сторону, противоположную скорости движения тела. При торможении тела о жидкость сила Стокса будет уменьшаться. При этом наступает такой момент, когда движение станет равномерным. Тогда уравнение движения примет следующий вид:

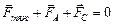. (1)

Зная направление действия сил, мы можем переписать уравнение (1) в скалярном виде. В проекциях на ось Ох получим:

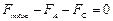. (2)

В наших опытах тело небольших размеров имеет форму шара. Поэтому, зная выражение для силы Стокса, действующей на шар 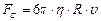, запишем уравнение движения в следующей форме:

, (3)

где 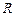– радиус шарика;

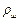и 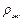– плотности шарика и жидкости;

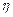– коэффициент вязкости жидкости; 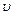– скорость движения шарика.

Таким образом:

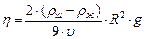. (4)

В уравнении (4) удобно ввести диаметр шарика и одновременно выразить его скорость через пройденный путь 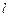и время , за которое этот путь пройден. Таким образом, получаем расчетную формулу для определения коэффициента вязкости жидкости методом Стокса:

. (5)

Дата добавления: 2014-12-08