Практическое занятие №2

Степеней подвижности этого механизма

.

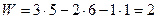Одна подвижность местная (вращение ролика 10 относительно собственной оси); основная подвижность W₀ = 1 реализуется в кулачковом механизме вращением кулачка 9, соединенного жестко с зубчатым колесом 8.

Индивидуальное задание. Определить степень подвижности механизма (рис. 2).

Рис. 2

Отчет по практическому занятию.

В ходе выполнения практического занятия изучена структура плоского механизма, определены состав его кинематических пар и степень подвижности, получены навыки проведения структурного анализа.

(Модуль «Синтез механизмов»)

Тема: «Зубчатые механизмы, их типы и синтез ».

Цель занятия: Изучение методики определения коэффициента полезного действия группы соединенных механизмов.

Продолжительность занятия: 1 час.

Вопросы для подготовки к занятию.

1. Что называют коэффициентом полезного действия машины?

2. Перечислите все виды соединений механизмов, входящих в один агргат.

3. Какое соединение механизмов называется смешанным?

Задача. Определить коэффициент полезного действия двух соединенных механизмов, привода барабанов складского рольганга (рис.3), если их к.п.д. η₁ и η₂ заданы.

Рис. 3

Методические рекомендации по выполнению задания.

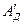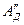Пусть работа движущих сил на валу рольгангов с учетом потерь в редукторе равна А_д. Часть этой работы идет на преодоление полезного сопротивления , а другая часть - на преодоление полезного сопротивления . Очевидно, что ; .

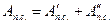Из выражений для отдельных КПД

;

можно написать

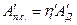и

После подстановки получим

Рассмотрим частные случаи:

1. При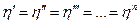

т.е. общий КПД равен каждому из частных значений.

2. При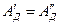

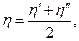
т.е. общий КПД равен среднему арифметическому частных к.п. д.

Индивидуальное задание.

Определить общий к.п.д. механизма по данным: η₁ = η₁ = η₁ = η₁ =0.95; 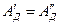. Ответ дайте числом.

Рис. 4.

Отчет по практическому занятию.

В ходе занятия была изучена методика определения коэффициента полезного действия механизмов, соединенных в группы последовательно, параллельно и смешанно.

Литература

1. Фролов К.В. Теория механизмов и машин. М., 2001.

2. Попов С.А., Тимофеев Г.А. Курсовое проектирование по теории механизмов и машин: Учеб. пособие для вузов. Под ред. К.В. Фролова. - М., 1998.

Занятие № 3

(Модуль «Основные методы решения задач

сопротивления материалов»)

Тема занятия: «Растяжение-сжатие стержней при осевом нагружении».

Цель занятия: Ознакомление со стержневыми системами. Изучение методов определения внутренних сил, построения эпюр внутренних сил, напряжений и перемещений. Определение из условия прочности размеров сечения, проверка стержня на прочность и жесткость.

Продолжительность занятия – 2 часа

Вопросы для подготовки к занятию:

1. Что мы называем стержнем?

2. В чем суть метода сечений?

3. Внутренние силы при осевом растяжении – сжатии.

4. Определение и размерность нормальных и касательных напряжений.

5. Закон Гука при растяжении – сжатии.

6. Правила построения эпюр внутренних сил, напряжений и перемещений.

7. Как определяются опасные сечения?

8. Три вида задач из условия прочности.

Задача: Для заданной схемы нагружения стержня, изображенной на

рис. 5а), осевыми нагрузками проверить опасные сечения (участок) на прочность, если задано: величина нагрузки F = 12,0 кН, площадь поперечного сечения участка стержня А = 150 мм²; допускаемое напряжение [s] = 170 МПа, модуль упругости при растяжении-сжатии Е = 2×10⁵ МПа, длина участка стержня а = 0,5 м.

Методические указания к решению задания:

- разбиваем стержень на участки;

- применяем метод сечений для определения нормальных сил;

- определяем напряжения на каждом из участков стержня;

- находим опасное сечение стержня и проверяем его на прочность;

- определяем перемещения на каждом участке стержня;

- строим эпюры нормальных сил, напряжений и перемещений стержня.

Данный алгоритм реализуем при решении задачи:

1. В начале решения стержень разбиваем на участки. Это разделение проводится с учетом изменения нагрузки или площади поперечного сечения стержня при переходе от одного участка к другому.

Для данной на рис. 1а) схемы нагружения стержня разбиваем его на три участка: первый - ВС; второй - СD и третий - DE.

2. Определяем нормальные силы (внутренние силовые факторы) на каждом из участков методом сечений. Для этого мысленно рассекаем стержень

а) б) в) г)

Рис. 5

плоскостью, перпендикулярной оси стержня, например I-I, на первом участке, отбрасываем одну из его частей и рассматриваем равновесие оставшейся части, проецируя все силы на вертикальную ось стержня. В нашем примере это нижняя часть стержня от точки В до плоскости I-I.

Знак нормальной силы в сечении определяется так: если нагрузка на данном участке направлена от сечения, то нормальная сила положительна, т.е. на этом участке стержень растягивается; в противном случае нормальная сила отрицательна, а стержень – сжимается. В нашем примере, на первом участке ВС нагрузка величиной 2F направлена от сечения I-I (рис.5а)), значит уравнение равновесия имеет вид:

N₁ – 2F = 0,

отсюда нормальная сила

N₁ = 2F = 2×12 = 24 кН,

т.е. на этом участке стержня имеет место его растяжение.

Применяя метод сечений на других участках стержня, получим:

- второй участок СD: N₂ = 2F = 2×12 = 24 кН – растяжение;

- третий участок DE: N₃ = 2F – F = F = 12 кН – растяжение.

3. Напряжение на каждом участке определяем как отношение нормальной силы к площади поперечного сечения стержня:

s₁= N₁ / (1,5 А) = 2F / (1,5A) = 2×12×10³/(1,5×150) = 106,7 МПа;

s₂ = N₂ / А = 2F / A = 2×12×10³/150 = 160,0 МПа;

s₃ = N₃ / А = F / A = 12×10³/150 = 80,0 МПа.

4. Определяем опасное сечение. Оно находится по наибольшей величине напряжения. В нашем примере это второй участок - CD, где каждое сечение является опасным, т.к.

s_max = s₂ = 160,0 МПа.

Согласно условию прочности при растяжении- сжатии в нашем примере имеем:

s_max = N _max /A £ [s],

отсюда s_max = 160,0 МПа £ 170,0 МПа.

Условие прочности выполняется.

5. Для определения перемещений 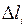на каждом участке применяем закон Гука, который имеет вид:

D ,

где N_i – нормальная сила на каждом i-том участке; L_i – длина каждого участка; Е – модуль упругости; S_i –площадь поперечного сечения каждого участка. В нашем примере получим:

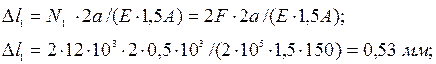
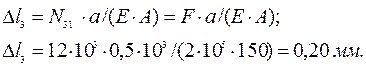
6. По проведенным расчетам строим эпюры, нормальных сил, напряжений и перемещений по длине стержня. Построение проводится от вертикальной нулевой линии в соответствующем масштабе. Эпюры штрихуют перпендикулярно нулевой линии. При построении эпюры перемещений следует учесть, что в заделке, т.е. точке Е, перемещение равно нулю. Построение эпюры перемещения проводится от этой точки по участкам, применяя равенство:

d =SD ,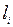

где суммирование проводится, считая от точки Е вниз по каждому участку:

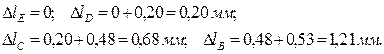
Построенные эпюры N, s, d приведены на рис.1б,в,г).

Индивидуальное задание.

D

F

E

C

B

1,5A

A

а

2а

Для заданной схемы нагружения стержня, изображенного на рис.6,

1,2а

осевыми нагрузками проверить опасные сечения (участок) на прочность, если задано: величина нагрузки F = 10,0 кН, площадь поперечного сечения участка стержня А = 100 мм²; допускаемое напряжение [s]= 170 МПа, модуль упругости при растяжении-сжатии

Е = 2×10⁵ МПа, длина участка стержня а = 0,5 м.

Рис.6

Отчет по практическому занятию.

Студент должен приобрести знания по основным понятиям сопротивления материалов и развить навыки расчета элементов конструкций на прочность и построении эпюр внутренних силовых факторов, напряжений и перемещений при растяжении-сжатии, что подтверждается решением индивидуального задания.

Дата добавления: 2014-12-08