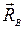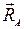Занятие № 6

(Модуль «Механические характеристики материалов.

Условия прочности. Рациональные сечения.

Тема занятия: «Плоский изгиб балок».

Цель занятия: Изучение деформации изгиба статически определимой балки с прямолинейной осью. Влияние способов опорного закрепления на определение опорных реакций. Построение эпюр поперечных сил и изгибающих моментов. Подбор заданного сечения из условия прочности. Дифференциальные зависимости при изгибе.

Продолжительность занятия – 2 часа.

Вопросы для подготовки кзанятию

1. Какие параметры определяют деформацию изгиб?

2. Виды опорных закреплений балок и реакции в опорах.

3. Внутренние силовые факторы при плоском изгибе.

4. Условия прочности при плоском изгибе.

5. Какие геометрические характеристики определяют напряжения и перемещения при изгибе.

Задача. Для заданной схемы нагружения балки (рис. 10) определить из условия прочности размеры сечения прямоугольной формы, если дано:

F = 6 кН, q = 8 кН/м, 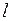= 4 м, ширина сечения (b) в два раза меньше его высоты (h), допускаемое нормальное напряжение [s] =120 МПа.

Методические указания к решению задания:

- составляем расчетную схему балки;

- определяем реакции опор балки;

- разбиваем балку на участки;

- применяем метод сечений на каждом из участков балки для определения поперечных сил и изгибающих моментов;

- определяем опасное сечение балки;

- находим из условия прочности балки размеры ее сечения;

- строим эпюры поперечных сил и изгибающих моментов.

Данный алгоритм реализуем при решении задачи:

1. Для составления расчетной схемы балки необходимо выполнить ряд построений (рис.6б). Начало плоской прямоугольной системы координат совместим с точкой А, ось абсцисс Х проведем по оси балки, а ось ординат из точки А вертикально вверх. Освобождаемся от связей в шарнирах и заменяем их реакциями 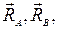направленными вверх. Равномерно распределенную нагрузку интенсивностью q, заменяем сосредоточенной нагрузкой величины 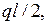приложенную к балке в середине отрезка АС и направим вектор этой нагрузки против оси ординат - вниз.

			B
			C

а)

		С

A

б)

		x2
			X

"Q(x)", кН

K

+

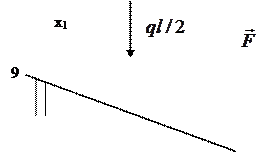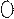
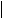
в)

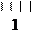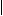
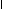
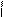
г)

Рис.10

2. Определяем опорные реакции. С этой целью удобно составить два уравнения моментов всех сил, действующих на балку, относительно точек А и В приложения неизвестных реакций:

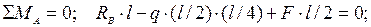
отсюда

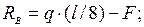
вычисляя, получим: 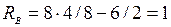кН;

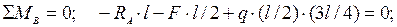
отсюда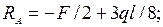

вычисляя, получим: 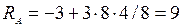кН.

Проверка: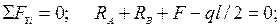

подставляя данные, получим: 9 + 1 + 6 – 8 × 4/2 = 0, т.е. 0 º 0,

значит реакции опор найдены правильно.

3. Разбиваем балку на два участка АС и СВ. Определяем поперечные силы Q(x) и изгибающие моменты M(x) на каждом участке. Для этого применяем метод сечений:

- первый участок АС. Положение сечения 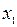изменяется следующим образом: 0£ 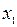£ 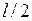. Записывая уравнения равновесия отсеченной части балки для поперечных сил и изгибающих моментов, с учетом правила знаков на (рис.11), получим:

	Q(x)
		Q(x)

–

M(x)

M(x)

–

+

+

			M(x)
	Q(x)

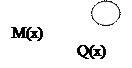Рис. 11

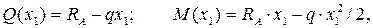
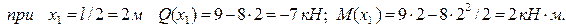
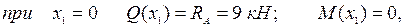
Поскольку поперечная сила на данном участке изменяет свой знак с плюса на минус, т.е. проходит через нуль, то согласно соотношению:

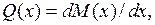
изгибающий момент должен иметь максимум в этом сечение. Определим координату " 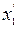", при которой 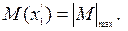В этом случае, выражение поперечной силы должно быть равно нулю:

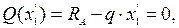
отсюда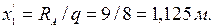

Тогда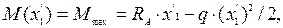

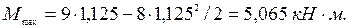
- второй участок (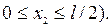 Начало координат переносим в точку В и рассматриваем равновесие отсеченной части, считая от точки В до сечения х₂:

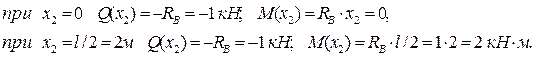
4. Определяем опасное сечение. С этой целью строим эпюры поперечных сил и изгибающих моментов (рис. 6в) и рис 6 г)). Опасным является сечение балки в точке К, где, изгибающий момент максимальный:

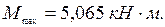
5. Размеры сечения балки определяем из условия прочности:

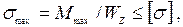
где 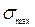– максимальное нормальное напряжение в опасном сечение балки;

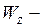осевой момент сопротивления сечения балки для заданного прямоугольного сечения балки:

,

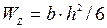выражая из условия прочности осевой момент сопротивления, получим:

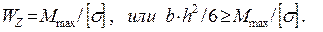
С учетом заданного соотношения высоты и ширины сечения h = 2b из последнего неравенства можно выразить b ширину прямоугольного сечения балки:

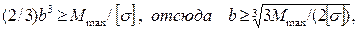
подставляя данные и округляя до стандартного значения, получим ширину сечения:

мм,

отсюда высота h = 2b = 80 мм.

Индивидуальное задание.

Для заданной схемы нагружения стальной балки (рис. 12) подобрать двутавровое поперечное сечение, если задано: q = 10 кН/м, М = 30кН×м,

F = 35 кН, а = 1м, [s] =120 МПа.

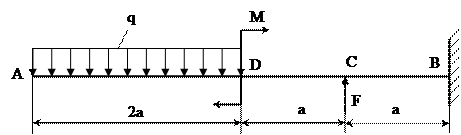Рис. 12

Отчет по практическому занятию.

Студент должен приобрести знания по разделу "Изгиб" сопротивления материалов и развить навыки расчета элементов конструкций на прочность и построения эпюр внутренних силовых факторов и напряжений при изгибе, что подтверждается решением индивидуального задания.

Дата добавления: 2014-12-08