Оценка трудоемкости поиска в случайном дереве

Древовидные таблицы

Явное использование структуры бинарного дерева позволяет быстро вставлять и удалять записи и производить эффективный поиск, и особенно целесообразно для организации динамических таблиц, подверженных частым вставкам и удалениям.

Рассмотрим простой метод построения дерева. Первую запись с ключом К₁ поместим в корень дерева. Второй ключ К₂ сравним с К₁. Если К₂ < К₂, поместим его в левое поддерево, а если К₂ ³ К₁, то в правое поддерево. В общем случае, когда требуется поместить в дерево i -йключ, поступаем так: сравниваем К_i с ключами, начиная с корня. Если К_i меньше очередного ключа, то переходим к левому сыну, в противном случае – к правому, а если соответствующий сын отсутствует, то это и есть место, куда нужно вставить ключ K_{i .} Пусть структура узла дерева:

struct NODE {

void *Record; // указатель на запись таблицы

NODE *Left, *Right;

};

Пусть int Cmp(const void *Record1, const void *Record2) – функция, выполняющая сравнение ключей записей *Record1 и *Record2. Функция традиционно возвращает значения <0,0,>0 соответственно в случаях ключ1<ключ2, ключ1=ключ2 и ключ1>ключ2.

Функция, выполняющая вставку новой записи в древовидную таблицу, приведена ниже:

const int LEFT=0;

const int RIGHT=1;

//----------------------------------

NODE *InsertRecord(NODE *Root, void *NewRecord){

NODE *x,*Cur,*Next;

int WhatSon; // каким сыном устанавливать новую запись –

// - левым (LEFT) или правым (RIGHT)

int CmpKeys; // результат сравнения ключей

x=new NODE;

x->Record=NewRecord;

Cur=Root;

// поиск места вставки

for(;;){

CmpKeys=Cmp(NewRecord,Cur->Record);

switch(CmpKeys){

case –1:

WhatSon=LEFT;

Next=Cur->Left;

break;

case 0:

case 1:

WhatSon=RIGHT;

Next=Cur->Right;

break;

}

if(Next==NULL){

break;

}

Cur=Next;

}

if(WhatSon==LEFT){

Cur->Left=x;

} else {

Cur->Right=x;

}

return x;

}

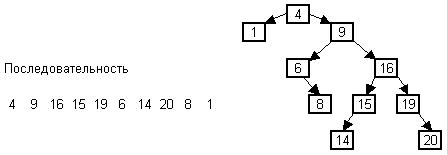
Рис 41. Результат вставки ключей в бинарное дерево

На рис. 41 изображен результат работы алгоритма.

Операция удаления узла. Сначала заметим, что обход бинарного дерева в обратном порядке даёт сортированную последо­ва­тель­ность. Все замечательные свойства древовидной таблицы связаны с этим обстоятельством. При удалении узла необходимо сохранить порядок следования узлов в обратном порядке. Легко удалить лист или узел, у которого пуста правая или левая связь. В общем случае одно из возможных решений таково: удалить следующий в обратном порядке узел, левая связь которого пуста, а затем вернуть его на место узла, который действительно требуется удалить. Ниже приведен текст функции, удаляющей узел, содержащий запись с целым ключом Key. Здесь предполагается, что дерево имеет голову, и, что само дерево является левым поддеревом головы. Голова содержит максимально возможное значение ключа. В случае успеха функция возвращает true.

struct NODE {

int Info;

NODE *Left;

NODE *Right;

int Rank; // для доступа по индексу

};

bool DeleteKey(NODE *Head, int Key){

// удалить Key из дерева с головой Head

NODE *Cur, *Next=NULL,*father=NULL;

// ищем узел, запоминая каждый раз отца

for(Cur=Head; Cur->Info!=Key && Cur!=NULL; Cur=Next){

if(Key<=Cur->Info){

Next=Cur->Left;

} else {

Next=Cur->Right;

}

father=Cur;

}

if(Cur==NULL){ // не нашли Key

return false;

}

// узел сur надо удалить

// может у Cur пуста правая связь?

if(Cur->Right==NULL){

if(father->Left==Cur){

// он левый сын своего отца

father->Left=Cur->Left;

} else {

// он правый сын своего отца

father->Right=Cur->Left;

}

delete Cur;

return true;

}

// поищем последователя с пустой левой связью

// шаг вправо и вниз до упора по левым связям

Next=Cur->Right;

father=Cur;

while(Next->Left!=NULL){

father=Next;

Next=Next->Left;

}

// Next - удаляемый узел

if(father->Left==Next){

// удаляемый узел - левый сын своего отца

father->Left=Next->Right;

} else {

// удаляемый узел - правый сын своего отца

father->Right=Next->Right;

}

Cur->Info=Next->Info;

delete Next;

return true;

}

Обозначим значения ключей, следующих в порядке возрас­тания k₁,k₂,…,k_n. Вероятность того, что в корень попадет ключ k_{i ,} равна 1/n. Тогда в левом поддереве будет i-1 узлов, а в правом n-i узлов. Пусть a_n – средний

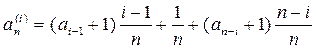уровень узла в дереве, содержащем n узлов. Тогда при условии, что ключ k_i находится в корне,

Выражение в правой части содержит три слагаемых:

1. искомый узел находится в левом поддереве с вероятностью (i-1)/n и средний уровень его равен a_i-1+1

2. с вероятностью 1/n это корень и его уровень 1.

3. с вероятностью (n-i)/n искомый узел находится в правом поддереве и средний уровень его a_n-i+1

Искомая величина a_n представляет собой среднее по i для всех

(1)

Отсюда следует: 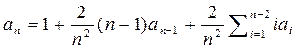(2)

а из (1) можно получить: 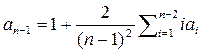(3)

Из (3) можно найти 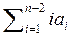, и, подставив это в (2), получим:

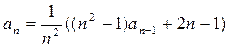(4)

a_n можно представить в виде: 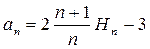(5),где . Справедливость (5) можно проверить непосредственной подстановкой (5) в (4).

По формуле Эйлера 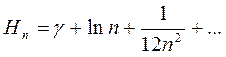, где 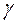- постоянная Эйлера, равная 0.571… Для больших n получим:

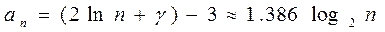
В заключение отметим, что, хотя среднее время поиска в случайном дереве пропорционально логарифму числа узлов, тем не менее, существует досадная

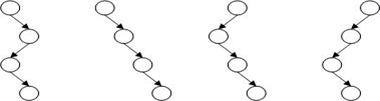возможность получения вырожденного дерева, время поиска в котором пропорционально числу узлов. Примеры таких деревьев приведены на рис.42.

Рис.42 Примеры вырожденных деревьев

Дата добавления: 2014-12-08