В-деревья

Представление линейных списков деревьями

Такое представление позволяет за логарифмическое время иметь доступ к узлу дерева как по ключу, так и по порядковому номеру. Для решения этой задачи в каждый узел дерева добавим новое поле по имени Rank. Это поле содержит порядковый номер узла при обратном обходе в дереве, которое из него исходит. На

рис.46 вместе со значениями ключей в скобках указаны значения поля Rank.

Рис. 46 Представление массива бинарным деревом

Ниже представлен текст функции, выполняющей поиск элемента массива по индексу. Алгоритм предполагает наличие головы у дерева. Собственно дерево является левым поддеревом головы.

struct NODE {

int Info;

NODE *Left;

NODE *Right;

int Rank;

};

//--------------------------------------------

NODE *FindByIndex(NODE *Head, int Index){

// найти узел по индексу (счет от 0)

int k;

NODE *Cur;

k=Index+1;

Cur=Head;

while(Cur!=NULL && k!=Cur->Rank){

if(k < Cur->Rank){

Cur=Cur->Left;

} else {

k-=Cur->Rank;

Cur=Cur->Right;

}

}

return Cur;

}

В-дерево - это структура, очень широко применяемая для поиска данных на внешнем носителе. Ее используют практически все существующие системы управления базами данных.

В-деревом порядка m называется дерево, обладающее следующими свойствами:

- каждый узел имеет не более m сыновей

- каждый узел имеет не менее m/2 сыновей

- корень, если он не лист, имеет не менее двух сыновей.

- все листья расположены на одном уровне

- узел, имеющий n сыновей, содержит n-1 ключей. Ключи расположены в узле в возрастающем порядке.

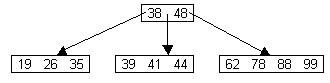
Рис.47 В-дерево

На рис 47. изображено В-дерево порядка 5. Связи как бы вставлены между ключами так, что указатель p_i указывает на поддерево с ключами К, такими, что K_i-1 < K < K_i. Узел, содержащий n ключей и n+1 указателей можно представить как на рис. 48.

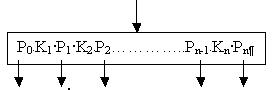
Рис.48 Узел В-дерева

Для В-дерева существует обобщение обратного обхода: сначала проходим поддерево, исходящее из P₀, затем ключ К₁, разделя­ющий поддеревья, исходящие из Р₀ и Р_1, затем поддерево, исходящее из Р_1, и так далее. Для дерева на рис. 47 обратный обход дает последовательность:

19 26 35 38 39 41 44 48 62 78 88 99.

Таким образом, обратный обход В-дерева дает сортированную последо­ва­тельность. Рассмотрим операции поиска, вставки и удаления.

Дата добавления: 2014-12-08