Термодинамика компрессорного процесса

Простейшая теория компрессорных машин, выражается по формуле

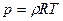(6.1)

При Конечном давлении воздушного компрессора более 10 МПа следует пользоваться уравнением реального газа

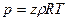(6.2)

где z – коэффициент сжимаемости, определяется опытным путем.

Основные уравнения. Совместное использование первого закона термодинамики и уравнения состояния идеального газа приводит к следующим уравнениям процессов сжатия и расширения, происходящих в компрессорах

Политропный процесс 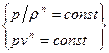(6.3)

Адиабатный процесс 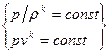(6.4)

Изотермический процесс 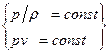(6.5)

Политропный процесс является общим видом термодинамического процесса и протекает в компрессорах в зависимости от внешних и внутренних условий с показателем п = 1,15 – 1,80.

Адиабатным называет процесс без теплообмена с окружающей средой; в таком процессе возможно внутреннее образование теплоты за счёт работы газового трения и вихреобразования. Строго адиабатный процесс в компрессорах получить нельзя вследствие невозможности полной тепловой изоляции газового потока от окружающей среды.

Кроме процессов (6.3 – 6.5) в теории компрессоров рассматривается процесс изоэнтропийный, характеризующийся постоянством энтропии в результате отсутствия теплообмена с окружающей средой и внутреннего тепловыделения, обусловленного газовым трением в потоке. В реальных компрессорах изоэнтропийный процесс невозможен.

Диаграммы ST и pv. Указанные процессы удобно изображатьграфически в координатах TS (рис. 6.5).

Здесь представлены основные виды компрессорных процессов: политропный n<k, свойственный компрессорам с интенсивным водяным охлаждением (рис. 6.5, а);

Политропный n>k, типичный для лопастных компрессоров (рис. 6.5, б);
изоэнтропийный с S=const (рис. 6.5, в);

Изотермический с Т= const (рис. 6.5, г).

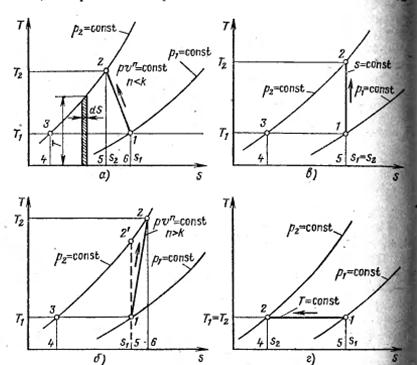
Рисунок 6.5 TS диаграммы компрессорных процессов по формулам (6.3 – 6.5)

Процессы на рис. 6.5, в и г в компрессорах неосуществимы, первый – потому что образование теплоты за счёт внутреннего газового трения проявляется весьма существенно, второй – по причине невозможности выполнить конструкцию охлаждающей системы компрессора так, чтобы она обеспечивала сжатие газа при постоянной температуре. Эти два процесса используются для оценки энергетической эффективности компрессоров.

Отметим свойства термодинамических диаграмм компрессорных процессов, показанных на рис. 6.5.

Процесс сжатия во всех случаях показан линиями 1 – 2. В случаях на рис. 6.5 а и б сжатие (повышение давления) сопровождается изменением энтропии и повышением температуры и увеличением энтальпии газа.

В политропном компрессорном процессе при n<k линия 1 – 2 представляет собой процесс сжатия, протекающий в рабочей полости (цилиндре, каналах колеса и корпуса) компрессоров; линия 2 – 3 – процесс изобарного охлаждения сжатого газа, уходящего из компрессора. Этот процесс протекает в охладителе компрессора и трубопроводной сети.

Работа, затрачиваемая компрессором на сжатие и выталкивание газа (без учёта механических потерь), представляется суммой теплот, отводимых от газа в процессах сжатия и изобарного расширения.

Воспользуемся основными определениями энтропии в элементарном тепловом процессе:

.

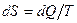Для процессов 1 – 2 и 2 – 3

; .

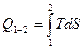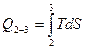Подынтегральные выражения являются элементарными площадями процессов сжатия и охлаждения, изображенных в TS – диаграмме. Следовательно, количество энергии в тепловых единицах, подводимое к газу для осуществления компрессорного процесса, представляется суммой площадей диаграммы 1 – 2 – 5- 6 и 2-3-4-5.

При сжатии газа по политропе с показателем n>k (рис. 6.5), что характерно для компрессоров с воздушным или интенсивным водяным охлаждением, площадь 1-2-6-5 под политропой 1-2 процесса сжатия представляет собой количество теплоты, образующейся в потоке вследствие газового трения и вихреобразования.

Энергия. Подводимая к компрессору, расходуется на проведение компрессорного процесса (сжатие и проталкивание) и работу газового трения в проточной полости. Работа компрессорного процесса представляется площадью 1-2-3-4-5. Следовательно, полная энергия, расходуемая компрессором (без энергии, идущей на покрытие механических и объёмных потерь), выражается площадью 2-3-4-6.

Если бы процесс протекал по изоэнтропе 1-2, то полная затрата энергии была бы равна площади 1-2 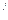-3-4-5, т.е. была бы меньше на размер площади 1-2 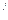-2-6-5. Следовательно, увеличение энергии, расходуемой компрессором, при переходе от изоэнтропийного процесса к реальному политропному с n>k сопровождается увеличением потребления энергии, равным площади 2 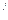-2-6-5-1. Площадь 1-2 -2 представляет собой энергию, затрачиваемую дополнительно на сжатие и проталкивание объема, появляющегося в результате нагрева газа в процессе трения и вихреобразования.

Изложенные соображения применимы и к рассмотрению TS – диаграмм изоэнтропийного и изотермического процессов (рис. 6.5, в,г).

Наименьшее количество энергии затрачивается в компрессорном процессе с изотермическим сжатием (рис. 6.5 г). Эта энергия представляется площадью 1-2-4-5.

В некоторых случаях удобно изображать компрессорные процессы на pv – диаграмме (рис.6.6). Здесь сплошной линией 1-2 показан процесс при политропном сжатии с n<k, протекающий в проточной полости компрессора. Процесс охлаждения 2-3 теоретически проходит по изобаре 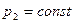, в действительных условиях несколько отклоняется от изобары.

Изотермическое сжатие изображается штриховой линией 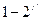, изоэнтропийное - 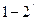, адиабатное при n>k линией .

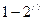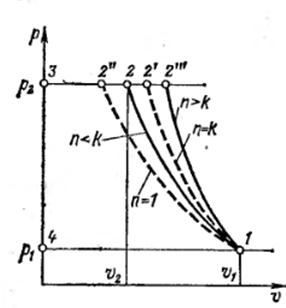
Рисунок 6.6 pv – диаграммы компрессорных процессов, по формулам (6.3 – 6.5)

Уравнение энергии компрессорных процессов. Энергия L, затрачиваемая компрессором при сжатии и выталкивании 1 кг газа, выражается площадью pv – диаграммы, ограниченной изобарами начального 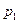и конечного 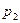давлений, политропой сжатия и осью ординат (рис.6.6).

Для процесса с n<k

.

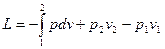После интегрирования и алгебраических преобразований получается формула (без вывода)

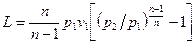(6.6)

Связь между давлениями и температурой в политропном процессе выражается формулой

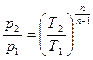. (6.7)

Поэтому

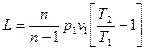(6.8)

Присоединяем к формуле (6.8) уравнение состояние, записанное для начальных параметров, .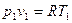

Тогда

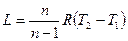(6.9)

Уравнение политропного и изоэнтропийного процесса (6.3) и (6.4) совершенно идентичны и разнятся только значениями показателей. Поэтому для изоэнтропийного процесса можно записать следующий формулы:

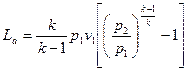; (6.10)

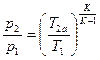; (6.11)

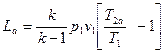(6.12)

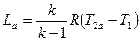(6.13)

Последняя формула преобразуется в уравнение с помощью соотношени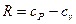й и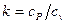

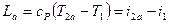(6.14)

Выражающее работу изоэнтропийного процесса через начальную и конечную энтальпии сжимаемости газа.

Для изотермического компрессорного процесса 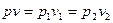и поэтому получается уравнение (без вывода)

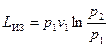(6.15)

Приведённые соотношения (6.6 – 6.15) позволяют определять затраты энергии на проведение компрессорного процесса, но не дают открытого ответа на вопрос о распределении израсходованной энергии на изменение отдельных параметров процесса.

Последнее может быть выполнено использованием условия сохранения энергии: энергия, расходуемая в компрессоре, идет на изменение энтальпии и кинетической энергии газа и покрытие потерь в окружающую среду. Это условие можно записать в общем виде как уравнение баланса энергии компрессорного процесса

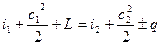(6.16)

или

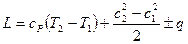(6.17)

В теории и расчётах компрессорных процессов принято использовать параметры торможения. Рассмотрим сущность этого понятия.

Если изоэнтропийный газовый поток с температурой Т и скоростью с полностью затормаживается, то его кинетическая энергия превращается в теплоту и температура газа повышается до 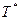, называемой температурой торможения. Соотношение баланса энергии

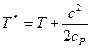(6.18)

Следовательно, в соответствии с (6.17) удельная энергия изоэнтропийного процесса может быть выражена через температуры торможения:

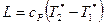(6.19)

Давления и температуры в изоэнтропийных процессах связаны соотношением (6.11). Поэтому параметр давления торможения может быть определен из этого уравнения:

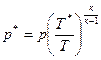(6.20)

Мощность компрессора

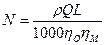, (6.21)

где 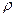- плотность газа, поступающего в компрессор, кг/м ; Q – объемная подача компрессора, м /с; L – удельная энергия компрессорного процесса, Дж/кг; 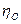- объемный коэффициент, учитывающий потери объема газа вследствие протекания через зазоры уплотнений компрессора; 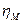- механический КПД компрессора, учитывающий расход энергии на преодоление механического трения и привод вспомогательных механизмов (масляных насосов, вентиляторов и насосов системы охлаждения).

Особенностью объемных компрессоров (поршневых и некоторых типов роторных) является периодичность их рабочего процесса, обусловленная периодичным движением рабочих органов. В рабочем процессе этих компрессоров следует выделить особую часть – политропное расширение газа от конечного до начального давления, предшествующее всасыванию газа в замкнутое рабочее пространство компрессора. Расширение газа обуславливает часть энергии, израсходованной на сжатие и выталкивание обратно на вал компрессора.

Дата добавления: 2014-12-08