Пример расчета рамы на ударную нагрузку

Условие задачи

На раму, показанную на рис. 7.5, падает груз Q с высоты 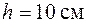. Вес груза 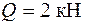, поперечное сечение рамы – двутавр № 20. Требуется найти максимальные нормальные напряжения в опасном сечении рамы и прогиб в точке удара от ударного действия нагрузки.

Решение

Чтобы определить динамический коэффициент по формуле (7.4), необходимо найти прогиб 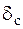точки С (точки приложения нагрузки Q) от статического действия нагрузки. Найдем этот прогиб, используя метод Максвелла – Мора и интегрируя формулу Максвелла – Мора с помощью правила Верещагина. Для этого построим эпюры изгибающих моментов от нагрузки Q (рис. 7.6, а) и от единичной силы, соответствующей искомому перемещению (рис. 7.6, б). Перемножим эти эпюры по правилу Верещагина:

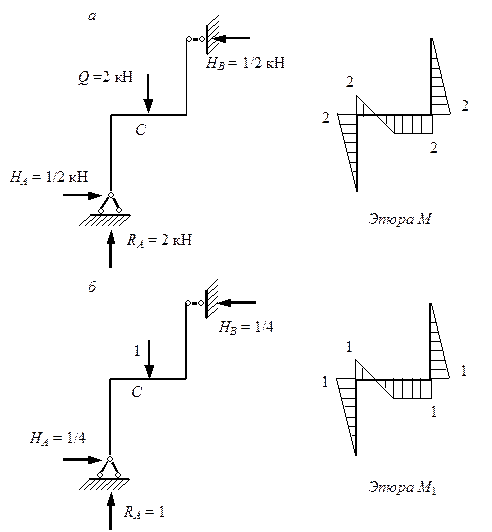  Рис. 7.6. Эпюры изгибающих моментов: а – от веса груза Q; б – от единичной силы

.

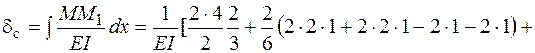
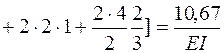Подставляя величину жесткости для двутавра № 20, сосчитаем прогиб в см:

.

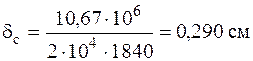Найдем динамический коэффициент по формуле (7.4):

.

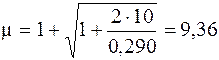Определим максимальные нормальные напряжения в опасном сечении от статического действия нагрузки. В рассматриваемом примере несколько равно опасных сечений с изгибающим моментом 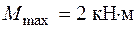. Максимальные статические напряжения

.

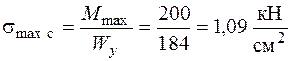Динамические напряжения от действия ударной нагрузки увеличатся согласно формуле (7.5) в 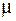раз:

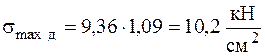.[23]

Во столько же раз увеличится и динамический прогиб:

.

СПИСОК ЛИТЕРАТУРЫ

Основная

1. Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995.

2. Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977.

3. Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989.

4. Сопротивление материалов: Метод. указания и схемы заданий к расчетно-графическим работам для студентов всех специальностей / СПбГАСУ; Сост: И. А. Куприянов, Н. Б. Левченко, Шульман Г.С.. СПб., 2010.

5. Сопротивление материалов: Учебное пособие по выполнению расчетно-графических работ. Ч. 1. / Н. Б. Левченко, Л. М. Каган-Розенцвейг, И. А. Куприянов, О. Б. Халецкая; СПбГАСУ. СПб., 2011.

6. Сопротивление материалов: Учебное пособие по выполнению расчетно-графических работ. Ч. 2. / Н. Б. Левченко; СПбГАСУ. СПб., 2011.

Дополнительная

7. Феодосьев В. И. Сопротивление материалов. М.: Наука, 1970.

8. Строительная механика. Под ред. Даркова А. В. М.: Высш. шк., 1976.

9. Иванов Н. М. Детали машин. М.: Высш. шк., 1998.

СОДЕРЖАНИЕ

Общие указания по выполнению расчетно-графических работ.....................

Используемые обозначения.......................................................................................

5. СЛОЖНОЕ СОПРОТИВЛЕНИЕ.......................................................................

5.1. Расчет балки, подверженной косому или пространственному изгибу................................................................................................................................

Пример расчета балки при пространственном изгибе (задача № 28)............................................................................................................

5.2. Внецентренное растяжение-сжатие стержней большой жесткости..............................................................................................................................

5.2.1. Определение моментов инерции сложных сечений относительно главных центральных осей (задачи № 29, 30, 31).................................................

Примеры решения задач................................................................................

Пример 1. Определение моментов инерции сечения, имеющего одну ось симметрии..................................................................................................................

Пример 2. Определение моментов инерции несимметричного сечения.......

5.2.2. Определение грузоподъемности жесткого стержня моносимметричного сечения при внецентренном растяжении-сжатии (задача № 29)...................

5.2.3. Определение грузоподъемности внецентренно сжатых жестких стержней несимметричных сечений (задачи № 30, 31)..........................................

5.3. Общий случай сложного сопротивления..................................................

Примеры решения задач......................................................................................

5.3.1. Расчет стержня в общем случае сложного сопротивления (задача № 32)...............................................................................................................

5.3.2. Расчет коленчатого вала на изгиб с кручением (задача № 33).............

Пример расчета коленчатого вала....................................................................

6. УСТОЙЧИВОСТЬ................................................................................................

Примеры решения задач.............................................................................................

6.1. Определение грузоподъемности центрально-сжатого стержня (задача № 34)..............................................................................................................

6.2. Подбор сечения центрально-сжатого стержня (задача № 35).....................

Пример 1...............................................................................................................

Пример 2................................................................................................................

6.3. Расчет гибкого сжато-изогнутого стержня (задача № 36)...........................

Пример расчета гибкого сжато-изогнутого стержня..........................................

7. РАСЧЕТ НА ДИНАМИЧЕСКУЮ НАГРУЗКУ...............................................

7.1. Вынужденные колебания систем с одной степенью свободы (задача № 37).............................................................................................................

Пример расчета системы с одной степенью свободы

7.2. Расчет рамы (балки) на ударную нагрузку (задача № 38)...........................

Пример расчета рамы на ударную нагрузку........................................................

Список литературы...............................................................................................

Нина Борисовна Левченко

Дата добавления: 2014-12-08