Рабочие углы инструмента

В процессе обработки, когда инструмент может быть закреплен на станке с погрешностями установки, а также, когда реализуются движения инструмента и заготовки, рабочие (действительные) углы инструмента отличаются от углов полученных в результате заточки.

а) Изменение углов в результате движения подачи D_s.

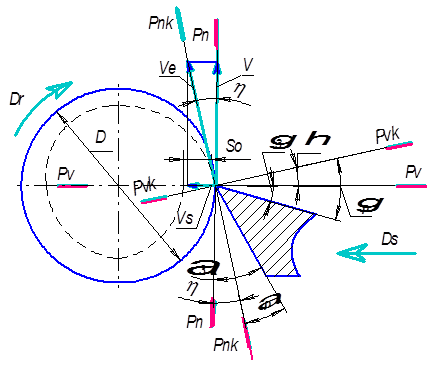
При операции отрезки (рис. 1.16) необходимо учитывать главное движение D_r и движение подачи D_s. В этом случае основная плоскость P_vк строится перпендикулярно относительно вектора результирующей скорости V_e, т.е. поворачивается против часовой стрелки на угол h. Поэтому, рабочий передний угол g_р будет больше, а рабочий задний угол a_р меньше углов заточки g_з и a_з на угол h.

; ,

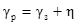где h - угол скорости резания.

Угол скорости резания h можно определить из соотношения

; (1.2)

откуда

, (1.3)

где S₀ – подача на 1 оборот детали, мм;

D – диаметр заготовки, мм.

g_р, a_р – рабочие кинематические передний и задний углы инструмента;

g_з, a_з – передний и задний углы заточки инструмента.

Рисунок 1.16 – Операция отрезки.

При продольном точении фасонной поверхности (рис. 1.17) происходит изменение направления движения подачи D_s. При этом изменяется положение рабочей поверхности P_s.

В результате этого поворота, рабочие кинематические углы в плане j_р в каждой точке являются переменными. Причем по сравнению с поз. 1, в поз. 2 угол j_р уменьшается, а j_1р увеличивается, в поз. 3 угол j_р увеличивается, а j_1р уменьшается.

Рисунок 1.17 – Продольное точение фасонной поверхности.

б) Изменение углов в результате погрешности установки.

Иногда в результате погрешности установки инструмента, вершина лезвия может быть расположена выше или ниже оси вращения заготовки (рис. 1.18). В этом случае также происходит изменение рабочих (действительных) углов по сравнению с углами инструмента, полученными после его заточки.

а) выше центра; б) ниже центра.

Рисунок 1.18 – Погрешность установки вершины лезвия относительно оси вращения заготовки.

Для приведенных случаев угол погрешности установки вершины резца относительно центра оси вращения установки x можно рассчитать по формуле

, (1.4)

где h – погрешность установки вершины лезвия, мм;

D – диаметр заготовки, мм.

Тогда при установке вершины резца выше центра рабочие (действительные) углы можно определить по зависимости

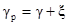, , (1.5)

а при установке ниже центра

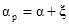, . (1.6)

В некоторых случаях резцы устанавливают не перпендикулярно оси вращения заготовки, изменяя тем самым значение углов в плане j и j₁.

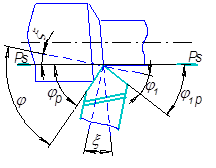
На рис. 1.19 показано изменение рабочих углов в плане при закреплении резца с углом погрешности x, значения которых можно рассчитать по формулам:

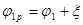, . (1.7)

Рисунок 1.19 – Схема изменения углов j и j₁ в зависимости от установки резца относительно оси заготовки

Дата добавления: 2014-12-08