В сопряжениях узлов трения 1 страница

4.1. Предельные износы по условию прочности

Для ряда деталей узлов трения, где допустимы сравнительно большие износы, критерием предельного состояния может служить уменьшение прочности детали при её износе.

Простейшим случаем влияния на прочность будет уменьшение размеров детали в результате её износа.

Соединение винт-гайка

Например, если толщина витка гайки а в соединении винт-гайка из-за износа U уменьшилась и стала равной а₁=а-U, то максимально допустимое значение износа [U] может быть подсчитано из условия расходования витком запаса прочности. При проектировании гайки был обеспечен запас прочности на срез n>1, так как допускаемые напряжения [ 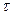] определялись по отношению к пределу прочности на срез 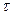_ср как

.

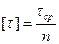Поскольку площадь среза равна S = al, где l – длина витка, можно записать, что

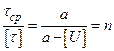. (4.1)

Это условие означает, что при достижении износом значения U =[U] имеющийся запас прочности n>1 будет исчерпан. Из равенства (4.1) получим

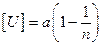. (4.2)

Пример 4.1. Определить допустимую величину износа витков гайки с резьбой УП440х48 нажимного механизма блюминга 1150, если запас прочности n=2.

Решение.

Определяем допустимую величину износа из зависимости (4.2)

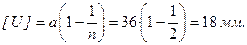
Толщина витка гайки:

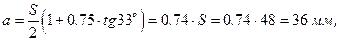
где S – шаг резьбы, мм.

Зубчатое зацепление

Используя аналогичный подход, определение значения максимально допустимой величины износа [U] для тихоходных зубчатых передач можно осуществить по зависимости:

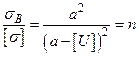; (4.3)

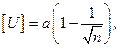(4.4)

где a – толщина зуба в основании;

s_В – предел прочности.

Для быстроходных зубчатых передач при определении [U] из условия прочности необходимо также учесть возрастание динамических нагрузок при увеличении зазора в зацеплении.

В этом случае зависимость (4.3) следует представить в виде

. (4.5)

Коэффициент динамичности находим из зависимости

, (4.6)

где С – жесткость наиболее податливого звена в линии привода;

М_с – статический момент сил сопротивления;

∆– зазор в сопряжении, равный:

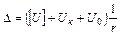, (4.7)

где [U] – допустимая величина износа зуба шестерни как наиболее изнашиваемой детали;

U_к – величина износа зуба колеса;

U_о – начальный зазор в сопряжении;

r – радиус основной окружности шестерни.

Величины U_к и [U] связаны зависимостью

(4.8)

где u – передаточное число передачи;

К=И_к/И_ш – коэффициент, равный отношению износостойкости колеса и износостойкости шестерни.

Подставляя значения К_д (4.6), ∆(4.7), U_к (4.8) и произведя небольшие преобразования, получим зависимость для определения максимально допустимой величины износа наиболее изнашиваемой детали в сопряжении

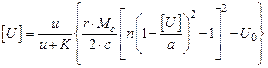. (4.9)

Значение [U] находят методом итерации, т.е. методом последовательных приближений, задаваясь начальным значением [U], добиваясь соблюдения равенства (4.9).

Пример 4.2. Определить допустимую величину износа шестерни реечного толкателя слябов. Модуль шестерни m=38, запас прочности n=1,2.

Решение.

Определяем допустимую величину износа шестерни из зависимости (4.4).

.

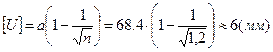Толщина зуба в основании a=1,8m=1,8*38=68,4 (мм)

Пример 4.3. Определить предельно допустимую величину износа зуба зубчатой втулки шпинделя линии привода валков пятиклетевого стана 1200 холодной прокатки. Исходные данные: передаваемый крутящий момент М_kp=98 кН ·м, длина шпинделя l=2185 мм, диаметр начальной окружности зубчатой втулки d=368 мм, m=8 мм, начальный зазор U_о=0,1 мм, запас прочности зубьев n=2.

Решение.

Для расчета воспользуемся зависимостью (4.9).

.

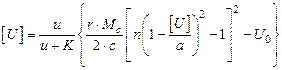Жесткость зубчатого шпинделя найдем по зависимости

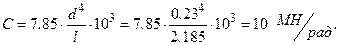
Приняв u=1, к=1 и [U]=1 мм, получим

.

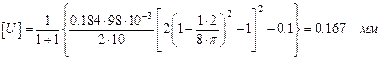Принимаем [U]=0.2 мм.

.

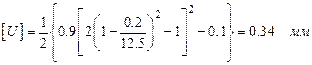Принимаем [U]=0.3 мм.

.

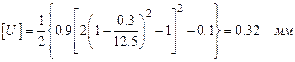Окончательно предельно допустимая величина износа составит 0.3 мм.

4.2. Предельный износ в подшипниках скольжения

В подшипниках скольжения, работающих в режиме жидкостной смазки, предельно допустимая величина зазора [D] при эксплуатации определяется из условия перехода из режима жидкостной в режим полужидкостной смазки, характеризующийся резким возрастанием интенсивности изнашивания

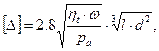(4.10)

где h_t – вязкость смазочного материала при рабочей температуре, Па ·с.

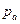– номинальное давление в подшипнике, Па;

w - частота вращения, с^-1;

d - диаметр подшипника, м;

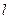– длина подшипника, м.

Наряду с этим важно знать, в каких пределах возможно изменение скорости, нагрузки, вязкости смазочного материала в любой момент времени, обусловленный соответствующей величиной износа.

Такие возможности характеризуются коэффициентом надежности подшипника c.

Граничным условием является

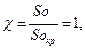(4.11)

где 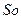, 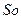_кр - число Зоммерфельда и критическое значение числа Зоммерфельда соответственно.

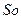_кр находится из зависимостей (7.3), (7.4) для значения x=0,1.

Если, например, c=3, то подшипник может выдержать в 3 раза большую нагрузку или работать на пониженной в 3 раза скорости, возможно понижение вязкости смазочного материала в 3 раза.

В действительности эти соотношения несколько иные, так как, например, с ростом нагрузки будет расти тепловыделение, снижающее вязкость масла.

Пример 4.4. Определить предельное значение нагрузки, скорости, диаметрального зазора и вязкости смазочного материала, при которых будет обеспечена надежная работа подшипников скольжения шестеренной клети реверсивной клети кварто 800/1400х2800.

Исходные данные:

диаметр подшипника d=600 мм;

длина подшипника l =820 мм;

нагрузка на подшипник Р=1.5 МН;

смазочный материал МС-14;

частота вращения 6-12 с^-1;

посадка подшипника Н7/е8.

Решение.

Находим предельно допустимый зазор из зависимости (4.10).

.

.

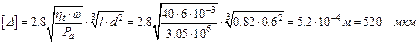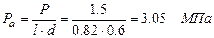Находим вязкость масла МС-14 при рабочей температуре подшипника из зависимости.

.

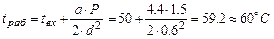Тогда

.

.

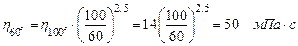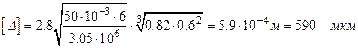Следовательно, предельно допустимая величина зазора в подшипнике равна 590 мкм при номинальной нагрузке и скорости.

Найдем коэффициент надежности подшипника.

;

.

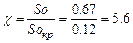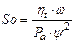Для посадки Н7/e8

.

.

.

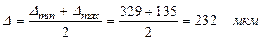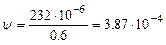Из зависимости (7.4) находим для ξ=0.1 и l/d=820/600=1.37.

.

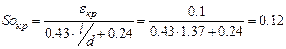Подшипник обладает большим запасом надежности. Но в процессе изнашивания его надежность снижается, и при увеличении зазора в 2 раза коэффициент надежности будет равен

;

.

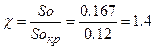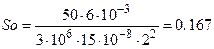При возрастании нагрузки в 2 раза:

;

;

;

.

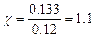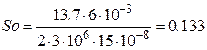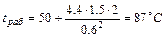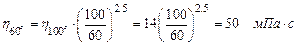Коэффициент надежности приближается к единице на изношенном подшипнике.

На изношенном же подшипнике перегрузки недопустимы при работе с частотой вращения 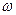= 6 с^-1.

4.3. Предельные углы перекоса

в валковой системе клети кварто

В валковой системе клети кварто из-за износа контактирующих поверхностей рабочих валков и в результате случайного комплектования подушками рабочих валков при их сборке возможно возникновение в рабочей клети перекоса осей рабочего и опорного валков, что ведет к появлению осевой силы А, воздействующей на элементы линии привода (рис. 4.1).

.Рис.4.1. Схема действия сил на площадке контакта при перекосе осей рабочего и опорного валков (а), и эпюра удельных сил трения вдоль оси опорного валка (б)

а

На рис. 4.1,б показана эпюра максимальных касательных напряжений на контакте рабочего и опорного валков. Ниже оси абсцисс показано изменение максимальной величины предварительного смещения по ширине площадки контакта 2а.

Площадь эпюры касательных напряжений характеризует величину осевой нагрузки в зависимости от угла перекоса валков .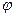

Значение удельной силы трения на участке предварительного смещения находим по зависимости из работы [13].

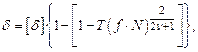(4.12)

где δ - текущее значение величины предварительного смещения;

Т, f – сила и коэффициент трения соответственно;

N - нагрузка;

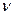- параметр шероховатости ( 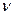=2).

Преобразуя зависимость (4.12), найдем величину удельной силы трения:

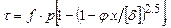(4.13)

где – контактное давление;

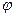- угол перекоса осей валков;

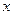– текущее значение ширины площади контакта.

При малых углах перекоса (до 1 ·10^-3 рад) для упрощения расчетов заменим образующую ОВа^/ прямой ОВС, проходящей через точку В, характеризующей величину удельных касательных напряжений на полуширине площадки контакта.

Тогда полное осевое усилие А найдем из уравнения

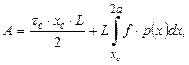(4.14)

где L – длина бочки валков;

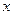_с – абсцисса точки С;

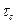– величина удельной силы трения в точке С, определяемая из зависимости:

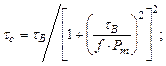
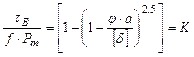. (4.15)

Значение касательного напряжения в точке В находим из зависимости (4.13), принимая х=а.

Полуширина площадки контакта а и значение максимального давления p_m находим по формулам Герца:

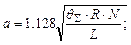
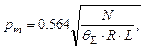(4.16)

где θ₁, θ ₂ – упругая постоянная материала рабочего и опорного валков соответственно; θ_S= θ ₁+ θ ₂, θ =4.3 ·10^-6 – для стальных валков, θ=6.3 ·10^-6 – для чугунных валков, МПа^-1; R – приведенный радиус валков.

Таблица 4.1

Радиусы кривизны вершин выступов

для поверхностей с различной обработкой

Вид обработки	Класс шероховатости	Радиус, мкм
поперечный rп	продольный rпр
Шлифование Точение	6-7 8-9 5-6 7-8	4-10 10-40 20-40 40-120	100-300 100-300 400-500 -
Фрезерование	4-5 6-7	30-60 60-80	400-500 -

Таблица 4.2

Ориентировочные значения параметров шероховатости

для различных видов обработки стальных поверхностей

Вид обработки	Класс шероховатости	Rmax, мкм	r, мкм	b	n	D
Круглое шлифование		9.4 4.7 2.4 1.2		0.6 0.9 1.3 2.0	2.0 1.9 1.9 1.9	1.6^.10^-1 4.1^.10^-2 9.6^.10^-2 2.8^.10^-2
Точение		9.4 4.7		1.0 1.4 1.8 2.0	2.1 1.9 1.8 1.6	2.5^.10^0 7.9^.10^-1 1.9^.10^-1 6.3^.10^-2

Таблица 4.3

Ориентировочные значения параметров шероховатости

для различных видов обработки чугунных поверхностей

Вид обработки	Класс шероховатости	Rmax, мкм	r, мкм	b	n	D
Круглое шлифование		7.2 3.5 1.8		0.70 1.20 1.25 1.55	1.9 1.9 1.8 1.7	2.72^.10^-1 6.5^.10^-2 2.0^.10^-2 7.5^.10^-3
Точение		7.4		1.10 1.20 1.45 1.50	1.9 1.8 1.7 1.6	1.85^.10^-1 5.4^.10^-1 1.54^.10^-1 4.4^.10^-2

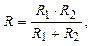(4.17)

R₁,R₂ – радиус рабочего и опорного валков соответственно.

Решая уравнение (4.14) совместно с (4.15), получим

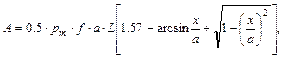(4.18)

где

. (4.19)

Величину [δ] находим по зависимости из работы [9] для условий насыщенного пластического контакта.

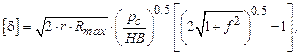(4.20)

где r – радиус микронеровностей, мкм;

R_max – максимальная высота микронеровностей (из табл. 4.1), мкм;

HB – твердость более мягкого из валков, МПа;

p_с – контурное давление, МПа.

Условие реализации насыщенного пластического контакта

р_C>0.062 HB. (4.21)

Для ненасыщенного пластического контакта

р_C<0.062 HB (4.22)

величина [δ] находится из зависимости (4.20)

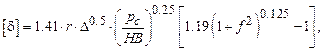(4.23)

где D - комплексная характеристика шероховатости (из табл.4.2, 4.3).

При малых углах перекоса осей валков (до 5 ·10^-4 рад) можно пользоваться упрощенной зависимостью

. (4.24)

Пример 4.5. Определить величину осевого усилия со стороны рабочих валков при неравномерном износе подушек рабочих валков.

Исходные данные:

перекос осей рабочего и опорного валка 1 ·10^-4 рад;

давление металла на валки 20 МН;

диаметры валков: рабочего 0.6 м, опорного 1.4 м;

материал рабочих валков – чугун, опорных – сталь;

расстояние между подушками рабочего валка l = 3 м;

твердость валка 3000 МПа;

характеристики шероховатости валка: r =20 мкм,R_vax =18 мкм;

коэффициент трения f =0,15.

Решение.

Величину осевого усилия находим из зависимости (4.24)

;

.

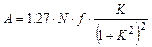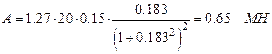Величину К находим из зависимости (4.15)

.

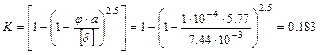Полуплощадку контакта "а" находим из выражения

.

.

.

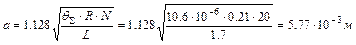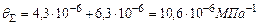Установим вид контакта

.

,

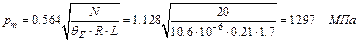что соответствует пластическому насыщенному контакту.

Тогда

Если величина А =0.69 МН является предельно допустимой из условия прочности элементов её воспринимающих, то разность в величине износа подушек

D=φ ·L_I =1 ·10^-4 ·3000=0.3 мм,

где L_I– расстояние между подушками валков, мм.

4.4. Предельный износ ролика транспортного рольганга

Транспортные рольганги широко используются в прокатных цехах для транспортировки металла между технологическими операциями. Причинами отказа роликов являются износ их поверхности вследствие абразивного изнашивания при соприкосновении с поверхностью транспортируемого металла, разрушение подшипников, износ полумуфты.

Вынужденная или плановая замена отдельных узлов роликов при эксплуатации приводит к тому, что в линии транспортного рольганга находятся ролики с разными диаметрами бочек. С тем, чтобы обеспечить один уровень транспортировки, под подушки роликов с меньшим диаметром бочек устанавливают прокладки.

Однако это не приводит к равенству окружных скоростей точек роликов, контактирующих с поверхностью транспортируемого металла, имеющего какую-то скорость V_м. Следовательно, ролики, имеющие больший диаметр бочки, будут стремиться проскальзывать относительно транспортируемого металла, а ролики, имеющие меньший диаметр, будут работать в тормозном режиме.

Как в первом, так и во втором случае при определенном соотношении диаметров наступает относительное скольжение поверхности роликов относительно транспортируемого металла и транспортируемого металла относительно поверхности роликов, что неизбежно ведет как к интенсивному изнашиванию, так и к повышенным потерям энергии на трение.

Поэтому необходимо знать, при какой величине в разнице износов бочек роликов начинается относительное скольжение поверхности бочки ролика и транспортируемого металла.

На рис.4.2 представлена схема к расчету допустимой величины разности износов бочек роликов.

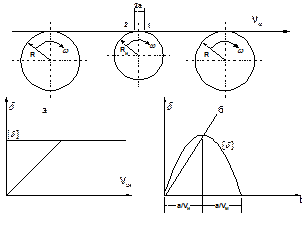
Рис.4.2. Расчетная схема к определению допустимой величины

износа бочки ролика:

а - условие начала скольжения контактных точек поверхности бочки ролика по полосе; б - условие начала скольжения поверхности бочки

ролика по полосе

Обозначим через R радиус бочки ролика, определенного из соотношения:

где V_м – скорость транспортируемого металла;

ω – угловая скорость роликов.

Обозначим через R_и радиус изношенной бочки валков

где [U] – допустимая величина износа поверхности бочки ролика, при которой начинается её скольжение относительно транспортируемого металла.

Тогда из рис. 4.2

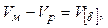(4.25)

где V_[δ] – скорость относительного смещения контактирующих точек поверхностей на выходе, при которой величина предварительного смещения достигает максимальной величины [δ].

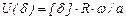(4.26)

где a - полуширина площадки контакта, определяемая по формуле Герца:

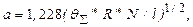
где q_S=q₁ + q₂

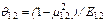- упругая постоянная контактирующих поверхностей;

m_1,2 - коэффициенты Пуассона;

Е_1,2 - модули упругости;

N - нагрузка;

l - ширина контактирующей поверхности бочки по длине ролика.

U_м – U_р = 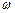(R – Rи) = 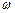[ U ]. (4.27)

Подставляя зависимости (4.26) и (4.27) в выражение (4.25), получим формулу для подсчета предельно допустимой величины износа:

[ U ] = [ 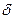] ·R / a. (4.28)

Максимальная величина предварительного смещения находится из зависимостей (4.23), (4.26).Учитывая,что

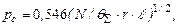
принимая НВ=1000 МПа, f = 0,3 для условий транспортировки горячекатаного металла при температуре 600 - 700°С, и подставляя в уравнение (4.28), найдем допустимую величину износа в случае ненасыщенного пластического контакта.

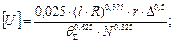(4.29)

где 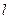и R - длина контакта и радиус бочки ролика, м;

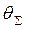- упругая постоянная, МПа^-1;

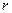- радиус микронеровностей, мм;

N - нагрузка на ролик, МН;

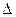- комплексная характеристика шероховатости поверхности бочки роликов.

Величину сил трения при частичном проскальзывании роликов по полосе можно найти из зависимости:

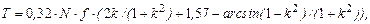(4.30)

где N - нагрузка на ролик;

f - коэффициент трения;

k – коэффициент;

,

, (4.31)

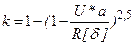
где U – величина износа бочки ролика.

При достижении износа бочки ролика предельно допустимой величины U =[U] величина силы трения будет равна

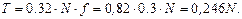
Тогда как при отсутствии проскальзывания роликов по полосе величина силы трения при транспортировке металла равна: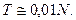

Таким образом, разница в диаметрах роликов ведет как к интенсивному их изнашиванию, так и к повышенному расходу энергии.

Пример 4.6. Определить предельно допустимую величину износа бочки ролика транспортного рольганга стана 2500 горячей прокатки.

Исходные данные:

диаметр бочки ролика D = 300 мм;

нагрузка на ролик N = 1 кН;

ширина полосы 1,5 м;

модуль упругости транспортируемого металла при

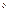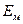t = 600 C, = МПа;

твердость горячего металла НВ = 1000 МПа;

поверхность бочки ролика обработана по 6-му классу чистоты обработки;

скорость транспортировки 10 м/с.

Решение.

Допустимую величину износа находим из зависимости (4.25).

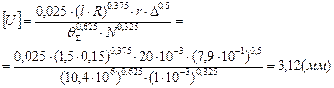
Определяем значение упругой постоянной :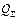

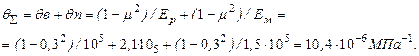
Значение радиуса микронеровностей r и комплексной характеристики шероховатости находим из табл. 4.2.

r = 20 мкм,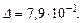

То есть при диаметре бочки ролика транспортного рольганга, превышающем средний диаметр роликов, находящихся в контакте с транспортируемым металлом, более чем на 6 мм, происходит проскальзывание поверхности роликов относительно транспортируемого металла.

В этом случае достигается максимальный расход энергии на преодоление сил трения, величину которых найдем из зависимости

Дата добавления: 2014-12-08