Дробно-рациональные функции, числитель и знаменатель которой представлен в виде многочлена второй степени

Дробно-рациональные функции, знаменатель которой представлен в виде мрогочлена второй степени.

Дробно-рациональные функции, числитель которой представлен в виде многочлена второй степени.

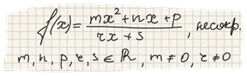
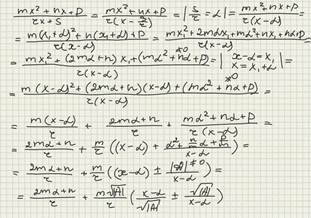
Базовые функции:

1) a (x)=x+1/x;

2) b (x)=x-1/x.

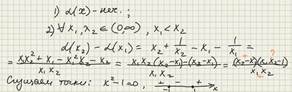
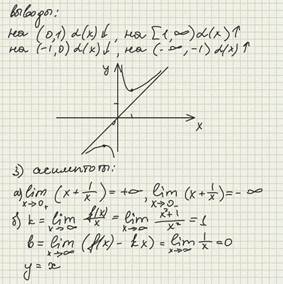
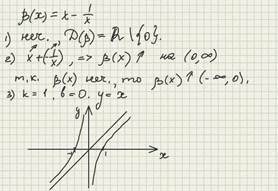
Параграф 5. Взимнообратные функции.

Определение 1. Функция называется обратимой, если равенство

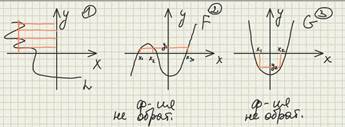
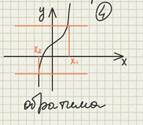
Замечание 1. Если функция чётная или периодическая, или нечётная, но переодическая, то эта функция не является обратимой.

Определение 2. Пусть функция y=f (x) задана на множестве X является обратимой функцией, и Y - множество её значений. Тогда на множестве Y может быть задана функция x=g (y) такая, что каждому значению y, принадлежащему Y, ставится в соответствие вполне определённое значение x из множества X, которое служит корнем уравнения y=f (x).

В этом случае функцию x=g (y) называют обратной функцией к фкнкции y=f (x).

Теорема 1. Всякая строоо монотонная функция обратима.

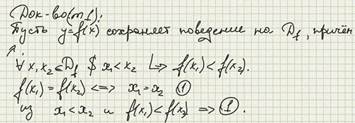
Следствие 1. Всякая сторого монотонная функция имеет себе обратную.

Замечание 2. Ошибочно считать, что только строго монотонные функции имеют себе обратную.

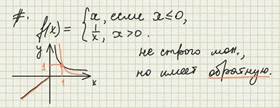
Теорема 2. Функция обратная к возрастающей является возрастающей функцией.

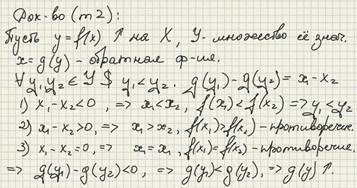
Теорема 3. Функция обратная к убывающей является убывающей.

Теорема 4. Графики взаимно обратных функций симметричны относительно прямой y=x.

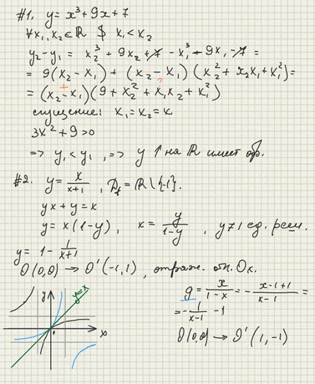
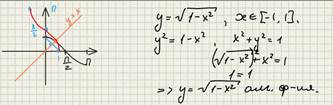
Параграф 6. Алгебраическая функция. Иррациональные функции.

Пусть задана целая рациональная функция. Зависимость между x, y обозначим P (x, y).

Определение 1. Уравеение вида P (x, y)=0 назовём алгебраическим. Оно определяет алгебраическую функциональную зависимость между x, y.

Определение 2. Если функция y=f (x) в некотором числовом промежутке удовлетвопяет алгебраическому уравнению, то она нащывается алгебраической функцией.

Алгебраические функции:

1. Целая рациональная функция является алгебраической.

2. Дробно-рациональная функция так же является алгебраической:

Теорема 1. Всякая дробно-рациональная функция является алгебраической.

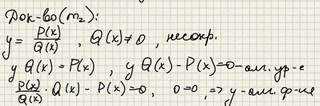
Определение 3. Всякая алгебраическая функция, которая не является рациональной, называется иррациональной функцией.

3. Иррациональные функции являются алгебраическими.

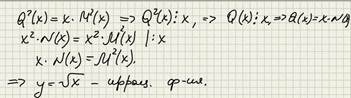
Базовые иррациональные функции.

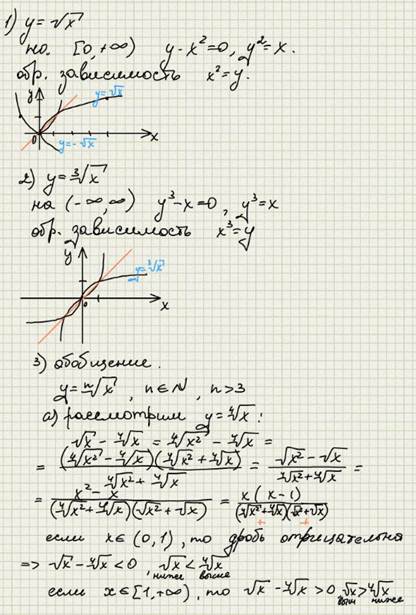
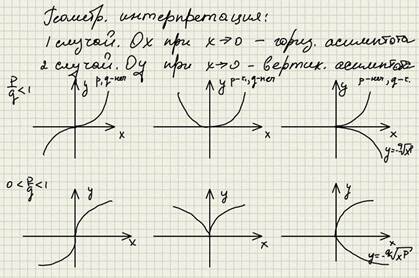
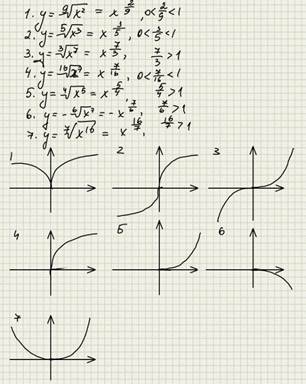
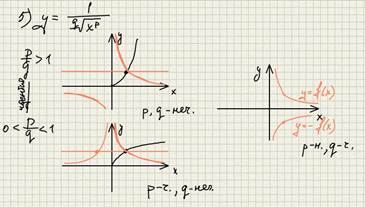
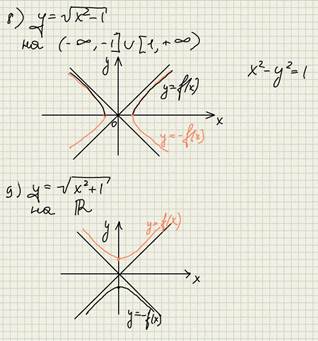
Параграф 7. Показательная функция.

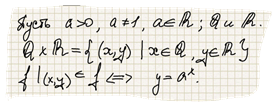
Так как каждому значению х соответствует единственное значение у, то f является функцией, которую мы будем называть показательной.

Рассмотрим свойства функции на множестве рационаььных чисел.

1. Для a> 1:

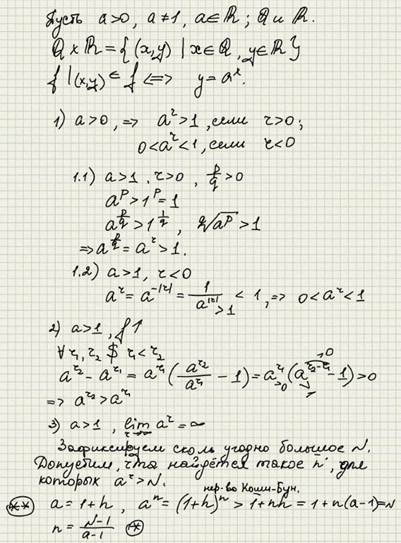
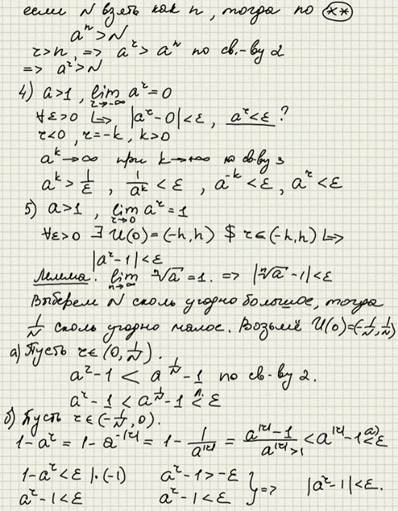
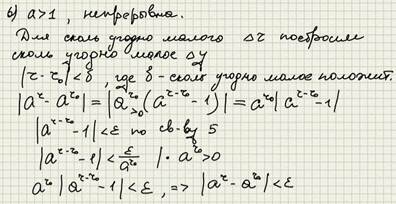
2. Для 0 <a <1

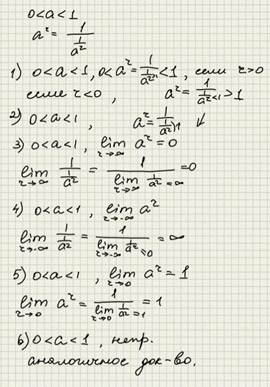
Показательная функция на множестве действительных чисел.

Было показано, что функция показательная определена и имеет значения в каждой точке-рациональное число. Необходимо доопределить функцию и найти её значение в каждой токе-иррациональное число.

Теорема. Если функция f (x), заданная в некоторой окрестности точки c, непрерывна в самой точке c, то значения функции в этой функции могут быт вычисленны, если известны, значения функции в каждой точке последовательности, которая имеет своим пределом точку c.

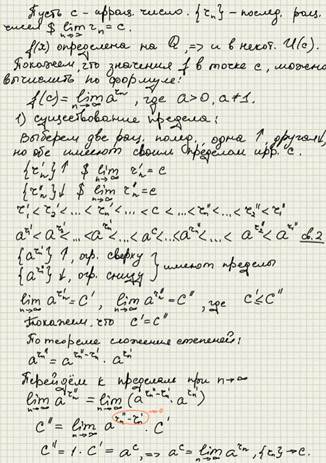
Чтобы все войства рассмотреть для показателя спенени в виде иррационаьного числа, нужно выполнить предельный переход, изображённый в теореме.

Изобразим график этой функции.

Исследуем функцию на выпуклость на всей области действительных чисел.

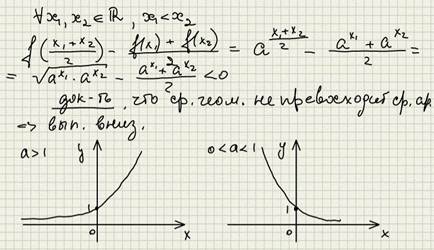
Параграф 8. Логарифмическая функция.

Определение 1. Логарифмом положительного числа b по основанию a,где a больше нуля и отлично от единице, называется показатель степени, при возведении в который число a получаем число b.

Основное логарифмическое тождество:

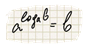
Теорема 1 (о существовании логарифма). Если a больше нуля и не равно единице, то существует единственное действительное число альфа такое, что a в степени альфа равно N, где N - наперёд заданное положительное число.

Доказательство.

Замечание 1. Логарифм нуля или отрицательного действительного числа не определяется, так как в основе понятия логарифма числа лежит значение показательной функции, которое только положительно.

Замечание 2. Логарифм с отрицательным основанием рассматриваться не будет в силу неоднозначности следующей операции:

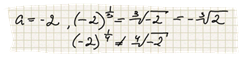
Замечание 3. Соотношение, которое получается на основе основного логарифмического тождества, является тождеством только для положительных x:

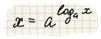
Свойства логарифма:

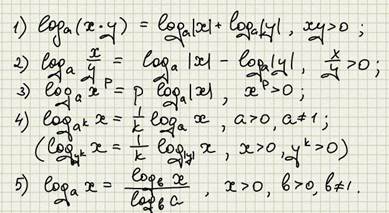
Определение 2. Логарифмической называют функцию, заданную формулой

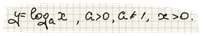
Свойства логарифмической функции:

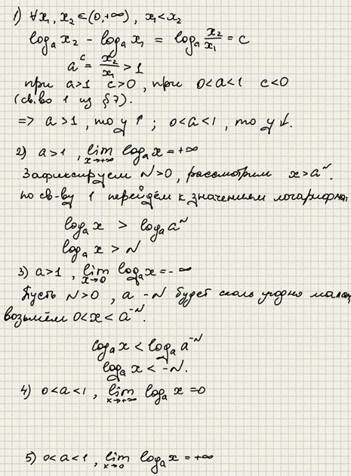
Параграф 10. Тригонометрические функции.

1. Основные тригонометрические функции.

Известно, что каждому числу х соответствует единственная точка на единичной окружности, получаемая поворотом точки (1, 0) на угол х радиан. Для этого угла определены sin x, cos x, тем самым каждому действительному числу х поставлено в соответствии числа sin x, cos x, то есть на множестве всех действительных чисел определены функции y=sin x, y=cos x. Областью определения будет всё множество действительных чисел.

Рассмотрим мнлжество значений.

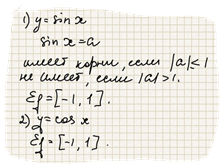
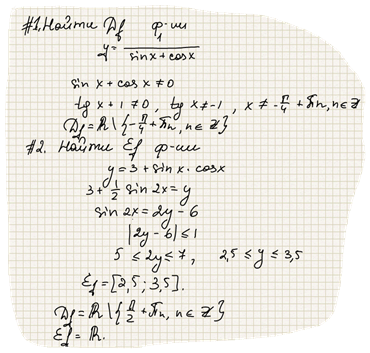
Областью определения функции y=tg x является множество чисел

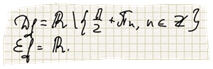
2. Чётность и нечётность, периодичность триоонометрических функций.

Каждая из функций sin x, cos x определена на множестве действительных чисел и для любого значния хверно равенство

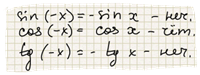
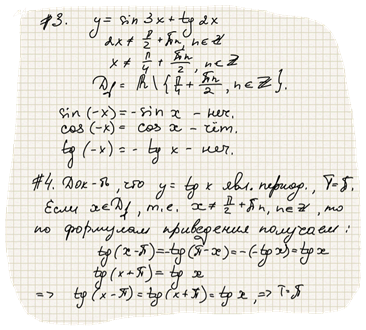
Определение 1. Функцию f (x) называют периодичесткой, если существует такое число Т, отличное от нуля, что для любого х из области определения этой функции, выполняется равенство

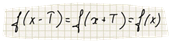
Число Т называется периодом функции.

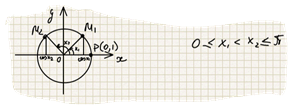
Следствие. Если х принадлежит области определения функции, то числа х+Тn, х-Тn также принадлежат области определения этой функции, где n принадлежит множеству целых значений.

3. Свойства функции y=cos x.

Функция y=cos x определена на множестве действительных чисел и областью значений является отрезок [-1,1]. Следовательно, график этой функции ограничен и лежит в полосе, между прямыми у=1, у=-1.

Так как эта функции имеет период 2П, то достаточно постоить её график на каком-нибудь промежутке длиной 2П.

Пострьив график функции на отрезке 0, 2П, мы можем построить график функции при помощи сдвигов на 2Пn, n принадлежит Z.

Функция является чётной, поэтому её график симметричен относительно оси Оу.

Для того, чтобы построить график на отрезке 0, 2П, достаточно построить его на отрезке 0, П, а затем симметрично отразить егь относительнт оси Ох.

Функция убывает на отрезке 0, П.

При повороте точки с координатами 1, 0 вокруг начала координат против часовой стрелки на угол от 0 до П абсцис точки, то cos x1 уменьшается от 1 до -1, поэтому если

,

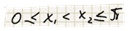то cos x1 > cos x2. Это означает, что функция убывает на отрезке от 0 до П.

4. Функция у=sin x.

Определена на всей числовой прямой, явьяется нечётной и периодической.

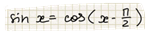
График функции можно получить при помощи параллельного переноса вправо на п/2.

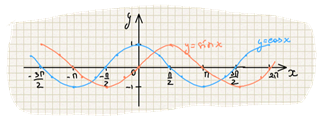
График такой функции называется синусоидой.

Основные свойства функции y=sin x:

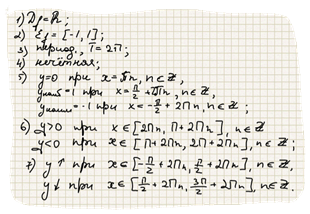
5. Свойства функции y=tg x.

Определена на всей числовой прямой, кроме х=п/2+2Пn, является нечётной и пертодической с периодом П. Поэтому достаточно построить её график на промежутке 0, п/2, затем отразить его симметрично относительно начала координат, получив график на промежутке -п/2, п/2, используя периодичность, построить на всей области определения.

Основные свойства функции:

6. Обратные тригонометрические функции.

Вспомним некоторые сведения из математического анализа.

Пусть функция y=f (x) задана на промежутке [a, b] и непрерывна на нём, тогда, опираясь на теоремы Больцано и Вейерштрасса, имеем следующие выводы:

1. Теорема Вейерштрасса. Для y=f (x) достигает в каких-то точках отрезка [a, b] своего наименьшего значения A и своего наибольшего значения B, где максимальное значение функции равно B и минимальное равно A, значения аргумента функции в этих точках принадлежат данному отрезку.

2. Теоремс Блльцано. Функция y=f (x) на отрезке [a, b] принимает, и, возможно, неоднократно, некоторое любое значение C, заключённое между значениями A, B. Тогда каково бы не было значение y из данного отрезка [A, B], уравнение y=f (x) имеет по крайней мере один корень x из отрезка [a, b].

Теперь сопоставим с каждым значением y из отрезка [A, B] все те значения x, которые служат корнями уравнения y=f (x), получаем обратную функцию x=g (y).

Рассмотрим функцию sin x, которая задана на промежутке от 0 до 2П, где функция непрерывна, значит достигает своего наибольшего и наименьшего значения в интервале от -1 до 1.

Некоторые значения функция принимает неоднократно.

Найдём корни уравнения y=sin x.

x1=arcsin y, x2=П-arcsin y. Теперь каждому значению у из интервала -1, 1 поставим в соответствие те значения х, которые стали корнями уравнения. Получим обратную тригонометрическую функцию x=arcsin y.

Теорема. Если функция y=f (x) строго монотонная и непрерывна на [a, b], то обратная функция x=g (y) однозначна строго монотонна в том же направлении и непрерывна на промежутке [A, B], где f (a)=A, f (b)=B.

Используя вывод этой теоремы, рассмотрим функцию y=sin x на промежутке о -П/2 до П/2, где она непрерывна и строго возрастает. Тогда существует, и при том только одна, одиночная обратная функция.

Определение 1. Arcsin x, x из [-1, 1], называется такое действительное число y из [-П/2, П/2], sin которого равен x.

График функции y=arcsin x получается из графика функции y=sin x. Надо провести прямую y=x и отразить от этой прямой часть синусоиды.

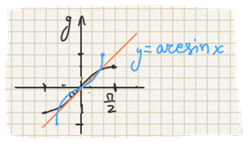
Свойства функции y=arcsin x:

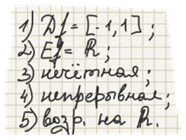
Определение 2. Arccos x, x из [-1, 1], называется такое действительное число y из [0, П], cos которого равен x.

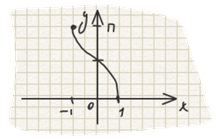
Свойства:

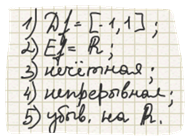
Определение 3. Arctan x называется такое действительное число y из [-П/2, П/2], tan которого равен x.

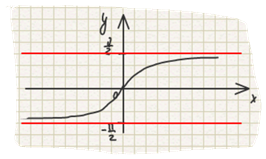
Свойства:

Определение 4. Arccot x называется такое действительное число y из [0, П], cot которого равен x.

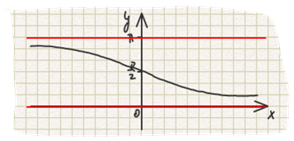
Свойства:

Тригонометрические функции связаны между собой большим количеством формул. Обратные тригонометрические функции чрезвычайно обогащают форменный аппарат тригонометрии, но пользоваться соотношениями, содержащие обратные функции, приходится, на самом деле, не очень часто. Математическая практика указывает, какие формулы заслуживают внимания:

1. Тригонометрическая функция от обратной тригонометрической функции есть алгебраическая функция.

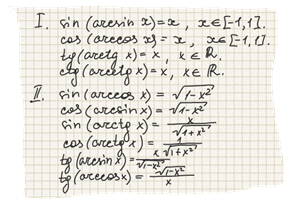
2. Обратная тригонометрическая от прямой есть бесконечное многозначное выражение, которое при несоответствии наименований может быть упрощено лишь в случае "ко-функции".

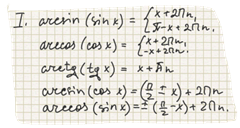
3. Одна обратная тригонометрическая функция связана с другой.

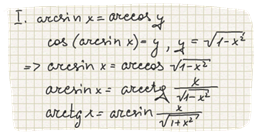
Дата добавления: 2014-12-08