Применение Excel для решения системы уравнений графическим методом

Решение системы уравнений графическим способом

Текст третьего задания третьей контрольной работы, в соответствии с номером вашего варианта, расположен в документе Задания к контрольной работе по информатике \ Задания_табличный процессор 4.doc.

В задании необходимо с помощью электронных таблиц произвести табуляцию функций, построить график и решить систему уравнений графически. Итоговый результат сохранить в файл под именем Табличный процессор 4.

Корнями уравнения являются значения точек пересечения графика функции с осью абсцисс. Решением системы уравнений являются точки пересечения графиков функций. Такой метод нахождения корней называется графическим.

При помощи табличного процессора можно решать уравнения и системы уравнений. Для графического решения подойдут средства построения диаграмм.

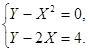Рассмотрим конкретный пример.

Найти решение следующей системы уравнений:

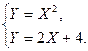Ответ записать с точностью до 0,1.

Преобразуем данную систему:

1. Для оценки решений воспользуемся диаграммой, на которой отобразим графики обеих функций. Для этого, на рабочем листе MS Excel создадим таблицу со следующими значениями (рисунок 1):

· 1 строка – строка заголовков;

· столбец А: заполняем ячейки А2:А22 числами от -10 до 10 с шагом 1;

· при заполнении столбца В в ячейку В2 заносим формулу =А2*А2, которую затем копируем до ячейки В22;

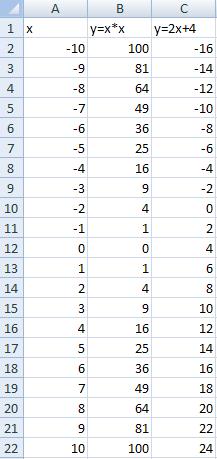
Рисунок 1 – Таблица с данными для приблизительного поиска решений

· при заполнении столбца С в ячейку С2 заносим формулу =2*А2+4, копируем ее до ячейки С22.

С помощью мастера диаграмм выберем тип диаграммы График и построим диаграмму первоначальной оценки решений (рисунок 2).

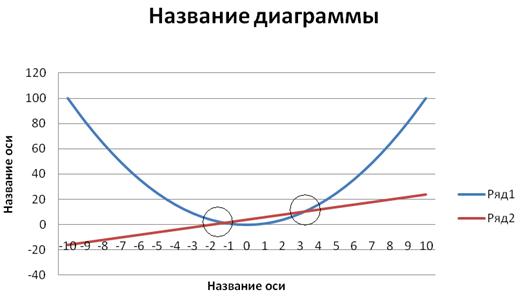
Рисунок 2 – Диаграмма первоначальной оценки решения

На рисунке 2 вы можете увидеть координаты точек пересечения графиков – решения системы. Однако, пока мы получили только приближенные значения решений.

Для уточнения значения решений построим графики в интервалах от -2 до 0, где находится первое решение, и от 2 до 4, где находится второе решение с шагом, 0,1 (рисунок 3).

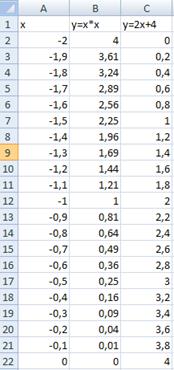
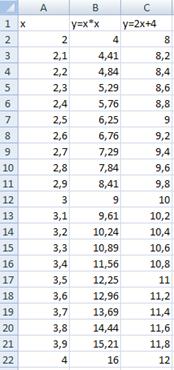
Рисунок 3 – Таблицы с данными для уточнения решений

2. Составляем новую таблицу для - 2 ≤ x ≤ 0. Строим точечную диаграмму для получения первого решения (рисунок 4).

Рисунок 4 – Поиск первого решения

3. Составляем новую таблицу для 2 ≤ x ≤ 4. Строим точечную диаграмму для получения второго решения (рисунок 5).

Рисунок 5 – Поиск второго решения

Решением нашей системы будут координаты точек пересечения графиков: x₁= -1,25; y₁= 1,5; x₂= 3,2; y₂= 10,8.

Графическое решение системы уравнений является приближенным.

Приложение 7

Дата добавления: 2014-12-08