Совокупность случайных величин

5.1. Закон распределения двумерной дискретной случайной величины

Системы случайных величин могут быть дискретными, непрерывными и смешанными, в зависимости от типа случайных величин, образующих систему.

Как и в случае одномерной случайной, полной вероятностной характеристикой многомерной случайной величины является закон распределения – соотношение, устанавливающее связь между областями возможных значений многомерной случайной величины и вероятностями её появления в этих областях.

Закон распределения может быть задан в различных формах. Например, если X и Y – дискретные случайные величины, то закон распределения двумерной случайной величины (X, Y) задается в табличной форме.

yj	xj
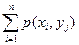
x1	x2	…	xj	…	xn
y1	p11	p21	…	pi1	…	pn1	p(y1)
y2	p12	p22	…	pi2	…	pn2	p(y2)
…	…	…	…	…	…	…	…
yj	p1j	p2j	…	pij	…	pnj	p(yj)
…	…	…	…	…	…	…	…
ym	p1m	p2m	…	pim	…	pnm	p(ym)
	p(x1)	p(x2)	…	p(xi)	…	p(xn)

Здесь

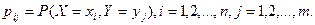
При этом

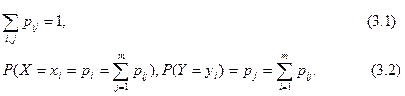
Если X и Y независимы, то =

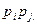
5.2. Функция распределения и плотность вероятностей двумерной непрерывной случайной величины.

Универсальной характеристикой многомерных случайных величин, пригодной для описания как дискретных, так и непрерывных случайных величин, является функция распределения.

В случае двумерной случайной величины функция распределения F₂(x,y) есть вероятность одновременного выполнения двух неравенств X<x, Y<y, рассматриваемая как функция переменных x, y:

F₂ (x, y) = P (X<x, Y<y) (3.3.)

В геометрической интерпретации (рис. 3.1) функцию распределения F₂(x,y) можно трактовать как вероятность попадания случайной точки внутрь бесконечного левого нижнего квадранта с вершиной (x,y).

Основное практическое значение имеют системы непрерывных случайных величин, распределение которых обычно характеризуют не функцией распределения, а полностью вероятности.

Если функция распределения F₂(x,y) непрерывна и обладает непрерывной смешанной производной второго порядка, то двумерная плотность вероятности определяется формулой

	Рис. 3.1. К определению функции распределения

	Рис. 3.2. Прямоугольная область		Рис. 3.3. Совместная плотность вероятности двух случайных величин и область

Функции F₂(x,y), p₂(x,y) обладают следующими основными свойствами:

1. F₂ (x, y) – неубывающая функция своих аргументов, т.е.

F₂ (x₂, y) ≥ F₂ (x₁, y), если x₂>x_1,

F₂ (x, y₂) ≥ F₂ (x, y₁), если y₂>y_1,

2. F₂ (x, -∞) = F₂ (- ∞, y) = F₂ (- ∞, -∞) = 0. (3.6)

3. F₂ (∞, ∞) = 1. (3.7)

4. F₂ (x, ∞) = F₁(x), F₂ (∞, y) = F₁ (y), (3.8)

Где F₁(x) и F₁(y) – соответственно функции распределения случайных величин X и Y.

5.

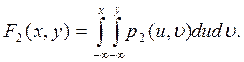
6. Вероятность P(R) попадания случайной точки (X, Y) в прямоугольник R (рис. 3.2.) со сторонами, параллельными осям O_x и O_y и с координатами вершин A(x₁,y₁), B (x₂,y₁), C (x₂,y₂), D(x₁,y₂) равна

(3.10)

7. . (3.11)

8. (3.12)

9. Вероятность P(D) попадания случайной точки в произвольную область (рис. 3.3.) определяется формулой

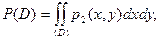(3.13)

где p₂ (x,y)dxdy – элемент вероятности для системы двух случайных величин.

5.3. Условные законы распределения.

Одномерные функции распределения и плотности вероятности выражаются через двумерные с помощью следующих соотношений:

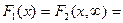
(3.15)

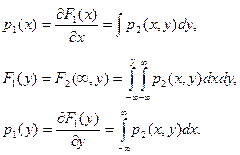
Закон распределения системы двух случайных величин X, Y определяется распределением каждой из величин, входящих в систему, и зависимостью между ними. Степень зависимости случайных величин X и Y характеризуется условным законом распределения, под которым понимается закон распределения одной из случайных величин, найденный при условии, что другая случайная величина приняла определенное значение.

По теореме умножения законов распределения

(3.16)

где

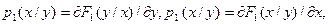
- условные плотности вероятностей.

Для независимых случайных величин X и Y

(3.17)

Условие (3.17) – необходимое и достаточное условие независимости случайных величин.

Выражения (3.15) и (3.16) позволяют получить соотношения, связывающие между собой условные и безусловные плотности вероятностей, а также формулу полной вероятности и формулу Байеса для непрерывных случайных величин: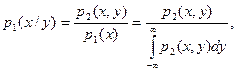

(3.18)

(3.19)

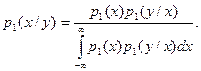(3.20)

Свойства 1-11 и формулы (3.1)-(3.20) обобщаются на многомерные случайные величины [1,13,16].

5.4. Числовые характеристики случайной величины.

Законы распределения являются исчерпывающими вероятностными характеристиками многомерных случайных величин. Однако если система включает в себя более двух –трех случайных величин, то экспериментальное определение её законов распределения весьма затруднено, а проведение расчетов требует громоздких математических вычислений. Поэтому при исследовании систем случайных величин широкое применение нашли их числовые характеристики, которые в определенной степени могут дать представление и о характере закона распределения. В основу получения таких числовых характеристик положено понятие моментов.

Различные моменты соответственно дискретных и непрерывных двумерных случайных величин определяются следующими формулами:

1. Начальный момент m_k1k2 порядка k_{1 +}k₂:

(3.21)

2. Центральный момент порядка k₁+k₂:

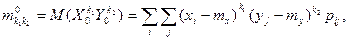
(3.22)

Из начальных моментов на практике наиболее часто используются начальные моменты первого порядка:

(3.27)

которые являются математическими ожиданиями случайных величин X и Y, входящих в систему, и которые определяют координаты точек, называемой центром рассеивания системы на плоскости.

Из центральных моментов наиболее употребительны моменты второго порядка. Два из них представляют собой дисперсии величин X и Y:

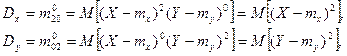(3.28)

характеризующие рассеивание случайной точки в направлении осей О_x и О_y.

Среди смешанных моментов особую роль играет центральный смешанный момент второго порядка 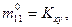называемый корреляционным моментом (иногда моментом связи) случайных величин X,Y:

(3.29)

Для дискретных случайных величин

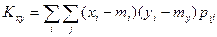(3.30а)

где

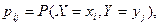
а для непрерывных

(3.30б)

Корреляционный момент K_xy описывает, помимо рассеивания величин X и Y, еще и связь между ними. Часто вместо K_xy пользуются безмерной величиной-коэффициентом корреляции R_xy:

(3.31)

где - средние квадратические значения величин X и Y. Коэффициент кореляции R_xy удовлетворяет условию: и определяет линейную вероятностную зависимость между случайными величинами.

Если X и Y независимы, то K_xy=0 и R_xy=0. Две случайные величины, для которых коэффициент корреляции равен 0, называются некоррелированными. Для гауссовских случайных величин некоррелированность означает также и независимость.

Дата добавления: 2014-12-08