Основы корреляционно-регрессионного анализа

Тема 6. Статистическое изучение связей и зависимостей

Все явления общественной жизни существуют не изолировано, а в неразрывной связи, т.е. зависят одно от другого. При этом выделяются факторные (х) и результативные (у) признаки.

Для количественных признаков зависимость между отдельными явлениями могут быть:

- функциональными, когда определенному значению одной переменной, фактору (х) отвечает четко определенное значение результативного признака (у);

- корреляционными (статистическими), когда с изменением факторного признака (х) изменяются групповые средние результативного признака (у).

Основным моментом в изучении связей между явлениями есть установление их сути на основе познания качественных характеристик явлений, их связей.

Наличие или отсутствие связей возможно выявить используя:

- метод аналитических группировок;

- графический метод;

- построение и анализ корреляционных таблиц;

- корреляционный анализ.

В корреляционно-регрессионном анализе линии регрессии имеются не в отдельных точках, как в аналитических группировках, а в каждой точке интервала изменения факторного значения (х). Линия регрессии изображается в виде определенной функции: у = f (x), которая называется уравнением регрессии, где у – теоретическое значение результативного признака.

Среди множества функций, наиболее распространенной в статистическом анализе является линейная 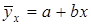, что объясняется простотой и содержательностью.

Для определения по данным парной корреляции параметров линейной регрессии надо решить систему нормальных уравнений для нахождения параметров а и b:

Иногда для нахождения параметров а и b используют способ определителей:

;

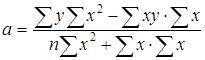После нахождения параметров (а и b) уравнения это уже не уравнение регрессии, а корреляционное уравнение, которое возможно использовать в прогнозировании результативного признака (у) при определенном значении фактора (х):

Методика расчетов изложена в таблице.

Таблица 3

№ п/п	Товарооборот, тыс. грн., х	Издержки обращения, тыс. грн., у	х^2	ху	у^2	Выравненное значение издержек обращения, тыс. грн.,
...

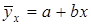
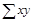
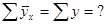
Дата добавления: 2014-12-08