Измерение тесноты связи

Измерить тесноту связи между коррелирующими величинами (х и у) можно при помощи корреляционного отношения (η) и коэффициента корреляции (r).

1. Корреляционное отношение применимо ко всем случаям корреляционной зависимости независимо от формы этой связи. Общий вид формулы корреляционного отношения

,

где η - корреляционное отношение;

η² - коэффициент детерминации.

В основе исчисления этих показателей лежит правило сложения дисперсий, согласно которому общая дисперсия (σ²) равная сумме межгрупповой дисперсии (σ²) и средней из групповых дисперсий ():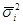

σ²= σ²+ σ²_i,

где 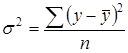, общая дисперсия, характеризующая влияние всех факторов на результативный признак (у);

, межгрупповая дисперсия, характеризующая влияние только изучаемого фактора (х) на результативный признак (у);

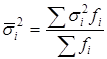, средняя из групповых дисперсий, характеризующая влияние прочих факторов на результативный признак (у);

- общая средняя;

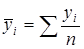- групповые средние;

n - число обследуемых данных в целом;

f_i - число обследованных единиц в каждой группе

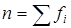
Корреляционное отношение может быть исчислено как:

- эмпирическое, на основе фактических данных

,

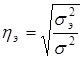- теоретическое исчисляется после нахождения параметров (а и b), т.е. после решения функций и нахождения теоретических (выравненных) значений результативного признака ()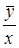

,

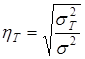где 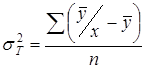, дисперсия теоретических значений результативного признака, характеризующая меру влияния факторного признака (х) на результативный ();

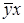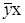- выравненное теоретическое значение результативного признака.

Поскольку: ,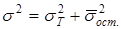

где 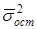– остаточная дисперсия, то η_Т может быть исчислено по формуле:

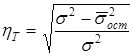
и носит название в этом случае индекса корреляции.

Чем ближе значение η к 1, тем больше зависимость между у и х. Чем ближе η к 0, тем зависимость меньше.

При:

η < 0,3 говорят о малой зависимости между коррелируемыми величинами;

0,3 < η <0,6 говорят о средней тесноте связи между х и у;

η > 0,6 говорят о большой (существенной) зависимости.

2. Линейный коэффициент корреляции (r), который используется как показатель тесноты связи только при линейной связи между х и у.

Его можно исчислить по формулам:

(1)

(2)

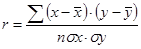(3)

,

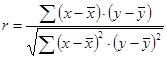где r – коэффициент корреляции, значение которого колеблется от –1 до +1 и характеризует не только тесноту связи, но и его направление (“-“ - обратная зависимость, “+” - прямая зависимость между х и у);

; ; ;

; ;

; ;

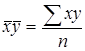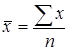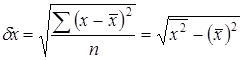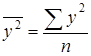n - количество признаков.

Для качественной оценки тесноты связи используют таблицу Чеддока:

Таблица 4

Значение коэффициента корреляции	0,1 – 0,3	0,3 – 0,5	0,5 – 0,7	0,7 – 0,9	0,9 – 0,99
Характеристика тесноты связи	слабая	умеренная	заметная	высокая	Весьма высокая

Из сути тесноты связи выплывает, что его численное значение может находиться только в границах ±1. Близость к 1 коэффициента корреляции говорит о близости к функциональной зависимости, а близость к 0 – о слабой зависимости.

Раздел 2. Статистика рынка товаров и услуг

Дата добавления: 2014-12-08