Прямой» метод расчета токораспределения в электрической сети

Метод расчета, основанный на применении уравнений 1 и II законов Кирхгофа без какого-либо их предварительного преобразования, может быть условно назвав «прямым» методом расчета сети. Задача расчета при этом заключается в определении токов в ветвях схемы на основании системы обобщенных уравнений

При решении задачи в такой постановке число уравнений в исходной системе может быть уменьшено, поскольку падение напряжения в ветвях 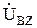не является при этом искомой величиной. Поэтому исходная система уравнений может быть принята в виде

В каждое уравнение системы (5-8) входит матрица искомых токов ветвей . Однако каждое из них, взятое отдельно, не позволяет найти эти токи, поскольку матрицы М и — не квадратные и, следовательно, для них не могут быть найдены обратные матрицы. Поэтому уравнения, входящие в систему (5-5), не могут быть преобразованы к форме, содержащей в левой части только матрицы искомых токов . Для определения токов должна быть, следовательно, использована система уравнений (5-8).

Обобщенная форма решения этой системы может быть получена, если воспользоваться понятием сложной матрицы. В рассматриваемом случае в качестве блоковых матриц (подматриц) следует принять М, , , 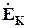. Тогда применительно к системе (5-8) можно написать

Применяя правило умножения матриц, нетрудно убедиться, что такая форма записи полностью соответствует системе матричных уравнений (5-8). В выражении (5-9) матрица

имеет квадратную форму, причем ее определитель не равен нулю. Такая матрица может быть обращена, и поэтому из выражения (5-9) можно найти

Дата добавления: 2014-12-08