Степенные ряды

Ряд

1 + 1/2^р + 1/3^р +..... + 1/п^р +......

называемый гармоническим, сходится (расходится) если р> 1 (р ≤ 1).

Сравнение рядов.

Пусть даны два знакоположительных ряда. Предположим, что каждый член одного из них не превосходит соответствующего члена другого.

ТЕОРЕМА (признак сравнения):

Если сходится ряд с большими членами, то и ряд с меньшими членами сходится.

Если расходится ряд с меньшими членами, то и ряд с большими членами расходится.

Теорема позволяет исследовать сходимость некоторых рядов, «сравнивая» их с рядами, с сходимости или расходимости которых уже известно.

Пример.

Исследовать сходимость ряда .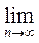

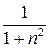Решение. Сравним данный ряд с гармоническим рядом 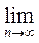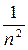, который сходится (р = 2 > 1): 1/ (1 + п²) <1 / п² 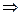данный ряд сходится.

Признак Лейбница.

Ряд а₁ – а₂ + а₃ –а₄ +...+ (-1)^п+1 а_п +......, где все числа а₁, а₂, а₃,

......., а_п,..... положительны, называются знакочередующимся..

ТЕОРЕМА (признак Лейбница сходимости знакочередующегося ряда):

Если абсолютная величина общего члена а_п стремится к нулю и монотонно убывает, то ряд сходится.

Пример. Исследовать сходимость ряда

1 – ½ + 1/3 – ¼ +.....+ (-1)^п+1/п +.....

Решение. А_п = 1/п монотонно убывает с ростом п и 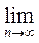(1/п) = 0 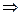ряд сходится.

Оценка погрешности приближенного вычисления

суммы знакочередующегося ряда.

Сумма всякого сходящегося ряда можно приближенно с любой степенью точности вычислить, заменив ее частичной суммой с достаточной большим номером (S ≈ S_п). При этом возникает вопрос об оценке погрешности.

Для ряда, удовлетворяющего условиям признака Лейбница, справедливо утверждение:

Погрешность меньше абсолютной величины первого отброшенного члена.

(| S – S | < а_п+1).

Пример. Для ряда, сходимость которого установлена в предыдущем пункте, найти сумму с точностью до 0,1,.

Решение:

S = 1 – ½ + 1/3 –..... + 1/9 – 1/10 +.....≈ 1 – ½ + 1/3 –.....+ 1/9 ≈ 1 – 0,5 + 0,333 – 0,25 + 0,2 – 0,167 + 0,143 – 0,125 + 0,111 ≈ 0,7.

Область сходимости функционального ряда.

Ряд f₁ (х) + f₂ (х) + f₃ (х) +.......+ f_п (х) +....., членами которого являются функции, называется функциональным.

Если вместо переменной х подставить какое-либо конкретное значение, то все функции f_п (х) примут определенные числовые значения и ряд превратится в числовой. Подставляя вместо х разные числа, получим разные числовые ряды. Часть из них будут сходящимися, другие – расходящимися. Отсюда получаем определение: множество значений х, при подстановке которых в функциональный ряд получается сходящиеся числовые ряды, называется его областью сходимости.

Получающиеся при различных значениях х, взятых из области сходимости, числовые ряды будут различными и, значит, будут иметь различные суммы. Таким образом, сумма функционального ряда есть функция от х.

Степенной ряд.

Функциональный ряд вида а₀ + а₁х + а₂х² + а₃х³ +....+ а_пх^п + а_п+1 х^п+1 +.

называется степенным.

(а₀, а₁, а₂,........, а_п, .......... – постоянные коэффициенты).

Число R = 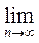|а_п/а_п+1 |

называется радиусом сходимости.

ТЕОРЕМА. Область сходимости степенного ряда состоит из интервала сходимости, -R < x < R и, может быть, одного или обоих его концов.

Пример на отыскание области сходимости см. в разделе «Образец решения контрольной работы», задача 1.26.

Дата добавления: 2014-12-08