Решение. 2 страница. В) обозначим как С событие, состоящее в ходя бы = ,

В) обозначим как С событие, состоящее в ходя бы = ,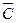

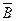Р(С) = 1 – Р(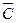) = 1 – Р( 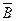) = 1 - Р() * Р(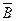) = 1 – (1 – 0,9) (1 – 0,8) = 0,98.

4.26. Дан закон распределения дискретной случайной величины Х:

Х	1 2 5
Р	0,5 0,3 0,2

Найти матожидание, дисперсию и среднеквадратическое отклонение Х.

Решение.

М [Х] = х₁ р₁ + х₂ р₂ + х₃ р₃ = 1 * 0,5 + 2 * 0,3 + 5 * 0,2 = 2,1

Д [Х] = (х₁ - М [Х])² р_{1 +} (х₂ - М [Х])² р₂ + (х₃ - М [Х])² р₃ = (1 – 2,1)² * 0,5 + (2 – 2,1)² * 0,3 + (5 – 2,1)² *0,2 = 2,29.

Σ [Х] = 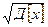= 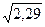≈ 1,513.

5.26. Известны матожидания α = 2 и среднеквадратическое отклонение σ = 4 нормально распределенной случайной величины Х. Найти вероятность того, что Х примет какое –нибудь значение в промежутке (1.10).

Решение.

Применим формулу: Р(α < X < β) = Ф () – Ф ()

Р(1 < X < 10) = Ф () – Ф() = Ф (2) – Ф (-0,25) = Ф (2) + φ (0,25)

≈ 0,4772 + 0,0987 = 0,5759.

Задание на контрольную работу

Задание № 1

Найти область сходимости степенного ряда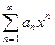

Номер варианта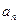
1.01	7 ^п / (п –1/2)
1.02	6 ^-п / (п –8/9)
1.03	3 ^п / (п –5/9)
1.04	5 ^-п / (п –7/8)
1.05	2 ^п / (п –3/4)
1.06	6^- ^п / (п –2/5)
1.07	9 ^п / (п –7/8)
1.08	6 ^-п / (п –3/4)
1.09	5 ^п / (п –2/3)
1.10	4 ^-п / (п –8/9)
1.11	7 ^п / (п –5/6)
1.12	6 ^-п / (п –3/8)
1.13	7 ^п / (п –2/9)
1.14	7 ^-п / (п –3/4)
1.15	6 ^п / (п –5/8)
1.16	9 ^-п / (п –2/7)
1.17	2 ^п / (п –4/9)
1.18	8 ^-п / (п –3/4)
1.19	6 ^п / (п –5/9)
1.20	3 ^-п / (п –1/2)
1.21	6 ^п / (п –5/7)
1.22	2 ^-п / (п –1/3)
1.23	2 ^п / (п –1/4)
1.24	6 ^-п / (п –5/7)
1.25	7 ^п / (п –4/5)
1.26	4^-п/(п – ¾)
1,27	4^п/(п – ½)
1,28	5^п/(п – 7/9)
1,29	5^-п/(п-2/7)
1,30	8^п/(п- ¾)
1,31	8^-п/ (п – 3/7)
1,32	3^-п/(п – 3/8)
1,33	5^п /(п – 2/3)
1,34	2^-п /(п – ½)
1,35	2^п /(п – ½)
1,36	3^п /(п – 7/9)
1,37	3^-п /(п – 7/9)
1,38	4^п /(п – 2/5)
1,39	4^-п /(п – 2/5)
1,40	5^п /(п – 2/7)
1,41	5^-п /(п – 2/7)
1,42	6^п /(п – 2/9)
1,43	6^-п /(п – 2/9)
1,44	7^п /(п – 3/5)
1,45	7^-п /(п – 3/5)
1,46	8^п /(п – 3/7)
1,47	8^-п /(п – 3/7)
1,48	9^п /(п – 4/7)
1,49	9^-п /(п – 4/7)
1,50	10^п /(п – 5/8)
1,51	10^-п /(п – 5/8)
1,52	11^п /(п – 3/8)
1,53	11^-п /(п – 3/8)
1,54	12^п /(п – 2/9)
1,55	12^-п /(п – 2/9)
1,56	15^п /(п – 3/7)
1,57	15^--п /(п – 3/7)
1,58	9^п /(п – 5/9)
1,59	9^-п /(п – 5/9)
1,60	8^п /(п – 4/9)
1,61	8^-п /(п – 4/9)

Задание №3

Решить задачи теории вероятности.

3.01. Вероятность прибытия в порт по графику первого судна равна 0,9; второго - 0,7. Найти вероятности того, что по графику прибудут а) оба судна, б) только одно, в) хотя бы одно.

3.02. В первом ящике 20 деталей, их них 4 бракованные, во втором - 5, их них 3 бракованные. Из каждого ящика наугад выбирают по детали. Найти вероятности того, что бракованными будут: а) обе детали, б) только одна, в) хотя бы одна.

3.03. В первой партии деталей 2% брака, во второй - 1%. Из каждой партии для контроля наугад выбирают по одной детали. Найти вероятности того, что бракованными будут: а) обе детали, б) только одна, в) хотя бы одна.

3.04. Вероятность своевременного прибытия на станцию первого поезда - 0,8; второго - 0,6. Найти вероятности того, что своевременно прибудут: а) оба поезда; б) только один; в) хотя бы один.

3.05. Вероятность попадания в цель при стрельбе из первого орудия равна 0,8; из второго - 0,7. Производится залп из двух орудий. Найти вероятности: а) двух попаданий; б) только одного, в) хотя бы одного.

3.06. Грузовая обработка судна может производиться одним из двух кранов. К моменту прихода судна первый кран освобождается с вероятностью 0,8; второй - 0,4. Найти вероятности того, что к приходу судна освободятся а) оба крана, б) только один, в) хотя бы один.

3.07. К моменту прибытия судна первый причал должен освободиться с вероятностью 0,8; второй - 0,3. Найти вероятность того, что к прибытию судна освободятся а) оба причала, б) только один, в) хотя бы один.

3.08. Станок-автомат штампует детали. Вероятность того, что за первую после наладки смену станок выпустит только стандартные детали, равна 0,7; а за вторую - 0,6. Найти вероятности того, что будут выпущены только стандартные детали а) в обе смены, б) только в одну из смен, в) хотя бы в одну.

3.09. Вероятность закончить в срок ремонт первого судна равна 0,9; второго - 0,6. Найти вероятности того, что в срок будет закончен ремонт а) обеих судов, в) только одного, в) хотя бы одного.

3.10. Производятся два последовательных выстрела по приближающейся мишени. Вероятность попадания при первом выстреле равна 0,3; при втором - 0,8. Найти вероятности а) двух попаданий, б) только одного, в) хотя бы одного.

3.11. Вероятность своевременного отправления в рейс для первого судна равна 0,7; для второго - 0,4. Найти вероятности того, что вовремя отправятся в рейс а) оба судна, б) только одно, в) хотя бы одно.

3.12. 90% ламп, изготавливаемых на первом заводе и 60% - на втором, имеют высокое качество. Наугад выбирают по одной лампе из продукции каждого завода. Найти вероятности того, что высокого качества будут а) обе лампы, б) только одна, в) хотя бы одна.

3.13. В первой бригаде успешно справиться с некоторым заданием могут 60%; рабочих, во второй - 40%. Наугад выбирают по одному рабочему из каждой бригады. Найти вероятности того, что с заданием успешно справятся а) оба рабочих; б) только один, в) хотя бы один.

3.14. Прибор состоит из двух узлов. Вероятность отказа при включении прибора для первого узла равна 0,2; для второго - 0,3. Найти вероятности того, что при включении откажут а) оба узла, б) только один, в) хотя бы один.

3.15. Охотник стреляет два раза по удаляющейся цели. Вероятность попадания при первом выстреле равна 0,7; при втором – 0,3. Найти вероятности а) двух попаданий, б) только одного, в) хотя бы одного.

3.16. Устройство состоит их двух элементов. При увеличении напряжения в два раза первый элемент выходит из строя с вероятностью 0,3; второй – 0,4. Найти вероятности того, что при повышении напряжения в два раза выйдут из строя а) оба элемента, б) только один, в) хотя бы один.

3.17. Рабочий обслуживает два станка. Вероятность нарушения в течение смены нормальной работы первого станка равна 0,1; второго - 0,2. Найти вероятности того, что в течение смены нарушения нормальной работы будут а) у обоих станков, б) только у одного, в) хотя бы у одного.

3.18. Всхожесть семян первого и второго сортов оценивается вероятностями 0,6 и 0,4. Посеяли по одному семени каждого сорта. Найти вероятности того, что взойдут а) оба семени, б) только одно, в) хотя бы одно.

3.19. В первом ящике 10 шаров, из них 3 черных, 7 белых; во втором ящике 10 шаров, из них 4 черных и 6 белых. Из каждого ящика наугад вынимают по шару. Найти вероятности того, что черными будут а) оба шара, б) только один, в) хотя бы один.

3.20. В электрическую цепь включены параллельно два элемента. Вероятность отказа в течение часа для первого элемента равна 0,1; для второго - 0,4. Найти вероятности того, что в течение часа откажут а) оба элемента, б) только один, в) хотя бы один.

3.21. В трюме судна установлены два аварийных сигнализатора, работающих независимо. Вероятность того, что при аварии сигнализатор сработает, равна 0,7 для первого и 0,9 для второго. Найти вероятности того, что при аварии сработают а) оба сигнализатора, б) только один, в) хотя бы один.

3.22. Проектировщик разыскивает формулу в двух справочниках. Вероятность того, что формула содержится в первом справочнике, равна 0,4; во втором - 0,3. Найти вероятности того, что формула содержится а) в обоих справочниках, б) только в одном, в) хотя бы в одном.

3.23. Вероятность того, что деталь нужного сборщику типа имеется в первом ящике, равна 0,6; во втором - 0,7. Найти вероятности того, что деталь нужного типа имеется а) в обоих ящиках, б) только в одном, в) хотя бы в одном.

3.24. Два исследователя проводят измерения некоторой физической величины. Вероятность того, что первый допустит ошибку при считывании показаний прибора равна 0,2; для второго - 0,1. Найти вероятности того, что ошибутся а) оба исследователя, б) только один, в) хотя бы один.

3.25. Вероятность успешного выполнения упражнения первым спортсменом равна 0,8; вторым - 0,9. Найти вероятность того, что успешно выполнят упражнение а) оба спортсмена, б) только один, в) хотя бы один.

3.26. Вероятность прибытия в порт по графику первого судна равна 0,7; второго - 0,9. Найти вероятности того, что по графику прибудут а) оба судна, б) только одно, в) хотя бы одно.

3.27. В первом ящике 20 деталей, их них 3 бракованные, во втором - 5, их них 4 бракованные. Из каждого ящика наугад выбирают по детали. Найти вероятности того, что бракованными будут: а) обе детали, б) только одна, в) хотя бы одна.

3.28. В первой партии деталей 1% брака, во второй - 2%. Из каждой партии для контроля наугад выбирают по одной детали. Найти вероятности того, что бракованными будут: а) обе детали, б) только одна, в) хотя бы одна.

3.29. Вероятность своевременного прибытия на станцию первого поезда - 0,6; второго - 0,8. Найти вероятности того, что своевременно прибудут: а) оба поезда; б) только один; в) хотя бы один.

3.30. Вероятность попадания в цель при стрельбе из первого орудия равна 0,7; из второго - 0,8. Производится залп из двух орудий. Найти вероятности: а) двух попаданий; б) только одного, в) хотя бы одного.

3.31. Грузовая обработка судна может производиться одним из двух кранов. К моменту прихода судна первый кран освобождается с вероятностью 0,4; второй - 0,8. Найти вероятности того, что к приходу судна освободятся а) оба крана, б) только один, в) хотя бы один.

3.32. К моменту прибытия судна первый причал должен освободиться с вероятностью 0,3; второй - 0,8. Найти вероятность того, что к прибытию судна освободятся а) оба причала, б) только один, в) хотя бы один.

3.33. Станок-автомат штампует детали. Вероятность того, что за первую после наладки смену станок выпустит только стандартные детали, равна 0,6; а за вторую - 0,7. Найти вероятности того, что будут выпущены только стандартные детали а) в обе смены, б) только в одну из смен, в) хотя бы в одну.

3.34. Вероятность закончить в срок ремонт первого судна равна 0,6; второго - 0,9. Найти вероятности того, что в срок будет закончен ремонт а) обеих судов, в) только одного, в) хотя бы одного.

3.35. Производятся два последовательных выстрела по приближающейся мишени. Вероятность попадания при первом выстреле равна 0,8; при втором - 0,3. Найти вероятности а) двух попаданий, б) только одного, в) хотя бы одного.

3.36. Вероятность своевременного отправления в рейс для первого судна равна 0,4; для второго - 0,7. Найти вероятности того, что вовремя отправятся в рейс а) оба судна, б) только одно, в) хотя бы одно.

3.37. 60% ламп, изготавливаемых на первом заводе и 90% - на втором, имеют высокое качество. Наугад выбирают по одной лампе из продукции каждого завода. Найти вероятности того, что высокого качества будут а) обе лампы, б) только одна, в) хотя бы одна.

3.38. В первой бригаде успешно справиться с некоторым заданием могут 40%; рабочих, во второй - 60%. Наугад выбирают по одному рабочему из каждой бригады. Найти вероятности того, что с заданием успешно справятся а) оба рабочих; б) только один, в) хотя бы один.

3.39. Прибор состоит из двух узлов. Вероятность отказа при включении прибора для первого узла равна 0,3; для второго - 0,2. Найти вероятности того, что при включении откажут а) оба узла, б) только один, в) хотя бы один.

3.40. Охотник стреляет два раза по удаляющейся цели. Вероятность попадания при первом выстреле равна 0,3; при втором – 0,7. Найти вероятности а) двух попаданий, б) только одного, в) хотя бы одного.

3.41. Устройство состоит их двух элементов. При увеличении напряжения в два раза первый элемент выходит из строя с вероятностью 0,4; второй – 0,5. Найти вероятности того, что при повышении напряжения в два раза выйдут из строя а) оба элемента, б) только один, в) хотя бы один.

3.42. Рабочий обслуживает два станка. Вероятность нарушения в течение смены нормальной работы первого станка равна 0,2; второго - 0,1. Найти вероятности того, что в течение смены нарушения нормальной работы будут а) у обоих станков, б) только у одного, в) хотя бы у одного.

3.43. Всхожесть семян первого и второго сортов оценивается вероятностями 0,4 и 0,6. Посеяли по одному семени каждого сорта. Найти вероятности того, что взойдут а) оба семени, б) только одно, в) хотя бы одно.

3.44. В первом ящике 20 шаров, из них 3 черных, 7 белых; во втором ящике 10 шаров, из них 4 черных и 6 белых. Из каждого ящика наугад вынимают по шару. Найти вероятности того, что черными будут а) оба шара, б) только один, в) хотя бы один.

3.45. В электрическую цепь включены параллельно два элемента. Вероятность отказа в течение часа для первого элемента равна 0,4; для второго - 0,1. Найти вероятности того, что в течение часа откажут а) оба элемента, б) только один, в) хотя бы один.

3.46. В трюме судна установлены два аварийных сигнализатора, работающих независимо. Вероятность того, что при аварии сигнализатор сработает, равна 0,9 для первого и 0,7 для второго. Найти вероятности того, что при аварии с работают а) оба сигнализатора, б) только один, в) хотя бы один.

3.47. Проектировщик разыскивает формулу в двух справочниках. Вероятность того, что формула содержится в первом справочнике, равна 0,3; во втором - 0,4. Найти вероятности того, что формула содержится а) в обоих справочниках, б) только в одном, в) хотя бы в одном.

3.48. Вероятность того, что деталь нужного сборщику типа имеется в первом ящике, равна 0,7; во втором - 0,6. Найти вероятности того, что деталь нужного типа имеется а) в обоих ящиках, б) только в одном, в) хотя бы в одном.

3.49. Два исследователя проводят измерения некоторой физической величины. Вероятность того, что первый допустит ошибку при считывании показаний прибора равна 0,1; для второго - 0,2. Найти вероятности того, что ошибутся а) оба исследователя, б) только один, в) хотя бы один.

3.50. Вероятность успешного выполнения упражнения первым спортсменом равна 0,9; вторым - 0,8. Найти вероятность того, что успешно выполнят упражнение а) оба спортсмена, б) только один, в) хотя бы один.

Задача №4

Дан закон распределения дискретной случайной величины Х. Найти матожидание, дисперсию и среднеквадратическое отклонение Х.

4.01.	Х	-3			4.02.	Х	-5
	Р	0,1	0,7	0,2		Р	0,3	0,6	0,1

4.03.	Х	-2			4.04.	Х	-4
	Р	0,5	0,4	0,1		Р	0,2	0,7	0,1

4.05.	Х	-1			4.06.	Х	-1
	Р	0,6	0,4	0,1		Р	0,4	0,5	0,1
4.07.	Х	-5			4.08.	Х	-4
	Р	0,1	0,6	0,3		Р	0,1	0,3	0,6

4.09.	Х	-1			4.10.	Х	-2
	Р	0,1	0,5	0,4		Р	0,1	0,4	0,5

4.11.	Х	-5			4.12.	Х	-2
	Р	0,5	0,4	0,1		Р	0,3	0,5	0,2

4.13.	Х	-1			4.14.	Х	-5
	Р	0,6	0,3	0,1		Р	0,6	0,1	0,3

4.15.	Х	-4			4.16.	Х	-6
	Р	0,2	0,3	0,5		Р	0,1	0,4	0,5

4.17.	Х	-2			4.18.	Х	-4
	Р	0,4	0,5	0,1		Р	0,1	0,6	0,3
4.19.	Х	-3			4.20.	Х	-5
	Р	0,2	0,7	0,1		Р	0,1	0,5	0,4

4.21.	Х	-3			4.22.	Х	-1
	Р	0,5	0,3	0,2		Р	0,5	0,1	0,4

4.23.	Х	-3			4.24.	Х	-4
	Р	0,5	0,2	0,3		Р	0,5	0,1	0,4

4.25.	Х	-3			4.26.	Х	-7
	Р	0,2	0,6	0,2		Р	0,1	0,6	0,3

4.27.	Х	-3			4.28.	Х	-5
	Р	0,1	0,4	0,5		Р	0,3	0,1	0,6

4.29	Х	-4			4.30.	Х	-3
	Р	0,6	0,2	0,2		Р	0,3	0,3	0,4

4.31.	Х	-1			4.32.	Х	-6
	Р	0,4	0,1	0,5		Р	0,2	0,2	0,6

4.33.	Х	-5			4.34.	Х	-6
	Р	0,2	0,6	0,2		Р	0,3	0,2	0,5

4.35.	Х	-5			4.36.	Х	-7
	Р	0,1	0,2	0,7		Р	0,2	0,5	0,3

4.37.	Х	-5			4.38.	Х	-6
	Р	0,1	0,7	0,2		Р	0,7	0,2	0,1

4.39.	Х	-5			4.40.	Х	-7
	Р	0,4	0,5	0,1		Р	0,3	0,4	0,3

4.41.	Х	-8			4.42.	Х	-4
	Р	0,4	0,3	0,3		Р	0,2	0,5	0,3

4.43.	Х	-4			4.44.	Х	-5
	Р	0,2	0,1	0,7		Р	0,4	0,2	0,4

4.45.	Х	-7			4.46.	Х	-2
	Р	0,3	0,2	0,5		Р	0,4	0,3	0,3

4.47.	Х	-2			4.48.	Х	-3
	Р	0,3	0,3	0,4		Р	0,3	0,4	0,3

4.49.	Х	-2			4.50.	Х	-5
	Р	0,1	0,8	0,1		Р	0,4	0,3	0,3

4.51.	Х	-5			4.52.	Х	-6
	Р	0,3	0,3	0,4		Р	0,1	0,8	0,1

Дата добавления: 2014-12-08