
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Входное сопротивление относительно точек: 5-6
|
|
|
|
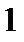
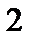
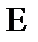
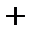

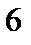
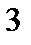

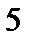
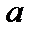
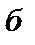 Включаем между точками 5-6 эдс
Включаем между точками 5-6 эдс 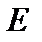 . А эдс ЕГ, так как ее внутреннее сопротивление равно нулю закорачиваем и получаем схему на рис.1.12.
. А эдс ЕГ, так как ее внутреннее сопротивление равно нулю закорачиваем и получаем схему на рис.1.12.
Рис.1.12 Схема для расчета входного сопротивления 
|
По тем же соображениям, что были рассмотрены выше 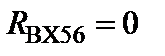
Очевидно для схемы по рис.1.6а, входное сопротивление относительно зажимов эдс равно сумме RЛ1 и RЛ2: 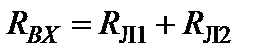
Для схемы по рис.1.6б, входное сопротивление относительно зажимов эдс равно: 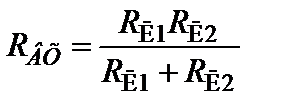 (параллельно соединенные резисторы).
(параллельно соединенные резисторы).
Для более сложных соединений резисторов следует придерживаться следующего порядка действий:
1. Включаем между точками, относительно которых ищется входное сопротивление, источник эдс.
2. Остальные источники эдс закорачиваем.
3. В полученной схеме сначала ищем последовательно соединенные сопротивления. Если есть, заменяем одним, равным сумме.
4. Затем ищем параллельно соединенные сопротивления. Если есть, заменяем одним по формуле для такого соединения.
5. Повторяем операции по пп. 3, 4 до тех пор, пока в схеме не останется одно сопротивление. Это и будет входное сопротивление.
Пример 1.2. Провести расчет схемы, показанной по рис.1.13 с использованием понятия входного сопротивления.
  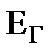 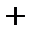 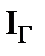 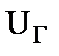 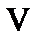   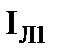  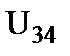 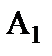 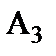 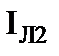  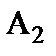 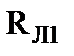 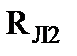 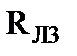
|
| Рис.1.13 Расчетная модель смешанного включения трех лампочек |
Находим входное сопротивление:
1. Ищем последовательно соединенные сопротивления. Таких нет.
2. Ищем параллельно соединенные сопротивления. Таких два: 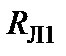 и
и 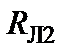 . Заменяем их одним:
. Заменяем их одним: 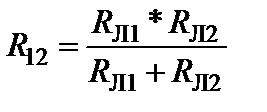 . Перерисовываем схему, убирая одно из сопротивлений, и ставим между узлами эквивалентное сопротивление
. Перерисовываем схему, убирая одно из сопротивлений, и ставим между узлами эквивалентное сопротивление 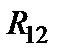 (рис.1.14).
(рис.1.14).
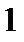 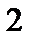 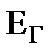  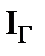 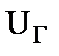 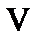  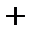  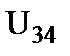 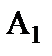   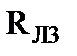
|
| Рис.1.14 Промежуточная расчетная модель |
Обратите внимание, что после проведенного преобразования не изменились значения тока 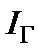 , потенциалы узлов 3 и 4, которые стали точками. Осталось неизменным и напряжение
, потенциалы узлов 3 и 4, которые стали точками. Осталось неизменным и напряжение 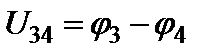 .
.
3. В полученной схеме резисторы 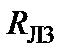 и
и 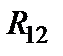 соединены последовательно, поэтому, объединяя их, получаем одно сопротивление, которое и будет равно входному сопротивлению:
соединены последовательно, поэтому, объединяя их, получаем одно сопротивление, которое и будет равно входному сопротивлению: 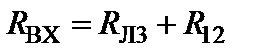 .
.
4. Расчет схемы, приведенной на рис.1.14 очевиден:
1. 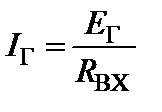 2. Находим напряжение
2. Находим напряжение 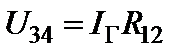 3. Находим токи
3. Находим токи 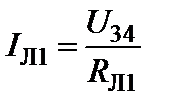
4. Находим токи 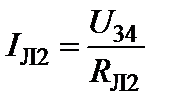
5. Составляем баланс мощностей.
Пример 1.3. Найти входное сопротивление в схеме, изображенной на рис.1.15 относительно точек А и Б.
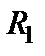  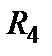 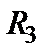 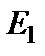 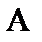 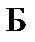
|
| Рис.1.15 Исходная схема для нахождения входного сопротивления |
1. Создаем расчетную модель для нахождения входного сопротивления:
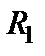

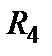
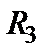
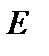
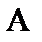
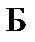
В полученной модели последовательно соединенных резисторов нет.
2. Ищем параллельно соединенные сопротивления. Таких имеется две пары: 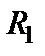 и
и 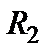 , а также
, а также 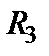 и
и 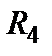 . Заменяем
. Заменяем 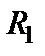 и
и 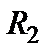 эквивалентным сопротивлениям
эквивалентным сопротивлениям 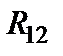 (рис.1.16):
(рис.1.16):
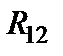 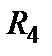 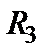 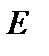 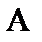 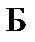
|
Рис.1.16 Схема после объединения 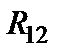
|
Объединяя резисторы 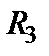 и
и 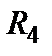 , получаем схему на рис.1.17:
, получаем схему на рис.1.17:
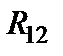 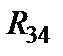 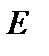 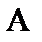 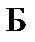
|
Рис.1.17 Схема после объединения 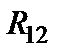 и и 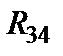
|
3.3 Очевидно, входное сопротивление относительно точек А и Б равно: 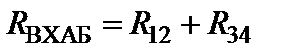 .
.
Рассмотрим схему, показанную на рис.1.18 и попробуем найти входное сопротивление относительно зажимов э.д.с. Е1.
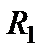 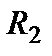 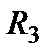 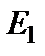 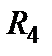 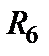 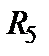
|
| Рис.1.18 Исходная схема для определения входного сопротивления |
Попытка найти последовательно и параллельно соединенные сопротивления будет неудачной. Тогда надо искать соединение треугольником или звездой. Так, в схеме имеется два треугольника: 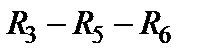 и
и 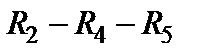 и звезды, одна из которых
и звезды, одна из которых 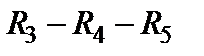 . Далее проводят преобразование одного треугольника в звезду, что существенно упрощает схему и позволяет проводить дальнейшее преобразование схемы, пока не будет найдено входное сопротивление. В рамках данного пособия это преобразование не рассматривается.
. Далее проводят преобразование одного треугольника в звезду, что существенно упрощает схему и позволяет проводить дальнейшее преобразование схемы, пока не будет найдено входное сопротивление. В рамках данного пособия это преобразование не рассматривается.
Читатель! Прежде чем двигаться дальше, проверьте себя. На рис.1.19 показана схема, содержащая резисторы и источник эдс. Готовы ли Вы ответить на следующие вопросы:
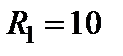 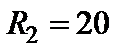  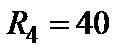 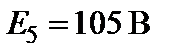 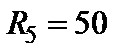 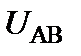 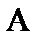 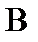
|
| Рис.1.19 Схема электрической цепи |
| № | Вопрос |
| Сколько узлов в схеме | |
| Сколько ветвей в схеме | |
| Сколько контуров в схеме | |
| Сколько уравнений можно составить по 1-ому закону Кирхгофа | |
| Сколько уравнений можно составить по 2-ому закону Кирхгофа | |
| Чему равно входное сопротивление схемы относительно т. А-В | |
Чему равно напряжение 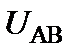
|
На отмеченные вопросы, ответы приведены ниже.
| № вопроса | Ответ | № вопроса | Ответ |
| 26,2 | |||
|
|
|
|
|
Дата добавления: 2014-11-28; Просмотров: 797; Нарушение авторских прав?; Мы поможем в написании вашей работы!