Лекция №5. Уравнение Бернулли и выводы из него

Уравнение Бернулли и выводы из него

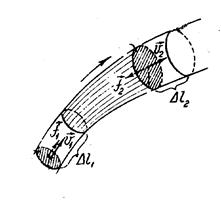
h2 h1 S2 S2 S1 S1 Рис.4.3

Выделим в трубке тока (рис.4.3) элемент, ограниченный плоскими сечениями S1 и S2. Пусть скорости движения жидкости в этих сечениях равны v1 и v2, а давления р1 и р2 соответственно. За время Dt выделенный элемент перемещается в направлении, указанном стрелкой, так, что сечения S1 и S2 cмещаются на расстояния D l 1 = v1Dt и D l 2 = v2 Dt соответственно, занимая новые положения и . При перемещении изменяется кинетическая и потенциальная энергии выделенного элемента. По закону сохранения энергии величина этого изменения определяется

работой сил давления f₁ = p₁S₁ и f₂ = p₂S₂, которые действуют на плоскости S₁ и S₂. Как видно из рис., часть элемента между сечениями и S₂ остается неподвижной так, что изменение положения выделенного элемента сводится к перемещению отрезка, ограниченного сечениями S₁ и в новое положение между плоскостями S₂ и . Пусть плотность жидкости в сечении S₁ равна r₁, а в сечении S₂ - r₂. Масса отрезка между сечениями S₁ и равна m₁ = r₁v₁S₁Dt, тогда как масса между S₂ и равна m₂ = r₂v₂S₂Dt; поэтому кинетическая и потенциальная энергии массы m₁ равны:

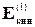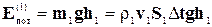= . (4-8)

Аналогично для массы m₂:

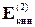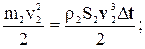
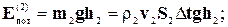= (4-9)

где h₁ и h₂ - высоты центров тяжести первого и второго элементов относительно выбранного уровня отсчета потенциальной энергии.

На основании закона сохранения механической энергии можно записать:

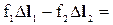
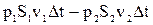= . (4-10)

Работа силы f₂ взята со знаком минус потому, что направление силы и направление перемещения противоположны друг другу.

Подставляя в уравнение (4-10) значения кинетических и потенциальных энергий (4-8) и (4-9), получаем:

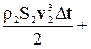
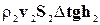
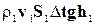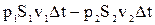= , (4-11)

откуда после сокращения на величину Dt (с учетом того, что v₁S₁ =v₂ S₂) следует:

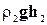
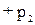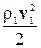
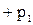= ,(4-12)

или в общем виде:

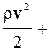
+ р = const. (4-13)

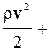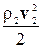
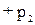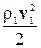
Выражения (4-12) и (4-13) представляют различные формы записи уравнения Бернулли, имеющего ряд важных следствий практического характера.Если движение жидкости или газа происходит на постоянной высоте, то уравнение (4-13) упрощается: р = const, или = 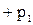. (4-14)

Из этого уравнения следует, что давление внутри трубки тока зависит от скорости: там, где скорость меньше, давление больше, при увеличении скорости потокадавление в нем уменьшается. Это утверждение называют принципом Бернулли.

Приложения уравнения Бернулли:подъемной силы крыла самолета, гидротрубина, гидротаран, водоструйный насос, аэрация почвы и т. д.

Основные характеристики и закономерности колебаний. Гармонические колебания. Сложение гармонических колебаний. Сложение перпендикулярных колебаний. Дифференциальное уравнение колебаний. Свободные колебания. Затухающие колебания. Энергетические соотношения в колебательных процессах. Колебания математического и физического маятников

Дата добавления: 2014-12-10