Уравнение вынужденных колебаний. Резонанс

Вынужденными называются колебания, которые происходят под действием внешней периодической силы. В этом случае частота колебаний не определяется параметрами самой системы, а задается внешним источником. Для груза на пружине уравнение движения может быть получено формальным введением в уравнение (5-20) еще одной - внешней периодической силы F(t) = F₀sin wt:

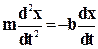+ mg - k (x +x) + F₀sin wt; (5-39)

после преобразований и обозначений, аналогичных прошлой лекции, получим:

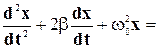f₀ sin wt, (5-40)

где f₀ = Остальные обозначения сохраняют свой смысл. Т.к. груз колеблется с частотой вынуждающей силы, решение дифференциального уравнения (5-40) может быть записано в следующем виде: x(t) = A sin(wt + j). Появление фазового сдвига между колебаниями груза и внешним воздействием связано с определенной инерционностью системы, реагирующей на внешнее воздействие с некоторым опозданием. Однако, для упрощения последующих выкладок, удобнее изменить начало отсчета сдвига фаз: пусть колебания груза происходят по закону x(t)=Asinwt, а внешняя сила получает некоторое опережение по фазе, т.е.f₀ sin(wt -j) = f (t) или заменяя j на (- y), f (t) = f₀ sin(wt +y). Тогда неизвестной величиной в выражении x(t) = Asinwt остается только амплитуда колебаний. Для ее определения используем векторный способ решения уравнения (5-40). Вычислим последовательно первую и вторую производные от х(t) и подставим эти производные в (5-40): = ; ; после приведения подобных получим:

2bwА f0   y   A( -w^2) Рис. 5.11

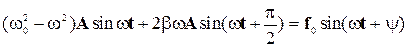.(5-41). Вспоминая, что колебания можно представлять в векторном виде, рассмотрим уравнение (5-41) как векторное: два вектора, стоящие в его левой части в сумме дают вектор в правой части (рис.). Из рисунка по теореме Пифагора следует: . Тогда , (5-42)

и . (5-43)

Из найденного выражения для амплитуды вынужденных колебаний (5-42) видно, что величина А зависит от частоты вынуждающего воздействия. Для нахождения экстремального значения этой амплитуды найдем производную знаменателя и приравняем ее к нулю: 4(, откуда следует, что «экстремальное» или резонансное значение частоты определяется как:

. (5-44)

Если частота внешнего воздействия может изменяться, то в тот момент, когда ее значение совпадает с w_рез , знаменатель (5-42) становится минимальным, а амплитуда вынужденных колебаний достигает максимальной величины. На практике очень часто наблюдается, что колеблющаяся система обладает слабым затуханием и b << w₀. В этом случае w_рез» w₀, т.е. значение резонансной частоты совпадает с собственной частотой системы. Явление возрастания амплитуды вынужденных колебаний до максимума, когда частота внешнего воздействия приближается к собственной частоте колебаний называется резонансом.

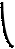А А рез 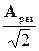    2Dw   w wрез Рис.5.12

Изменение амплитуды вынужденных колебаний в области частот, близких к резонансной - резонансная кривая - показана на рис.5.12. Чтобы оценить относительное изменение амплитуды при резонансе, необходимо знать величину амплитуды на двух частотах - на резонансной и на частоте, достаточно далекой от w рез. Рассматривая (5-42) нетрудно за- метить, что такой «далекой» частотой удобно выбрать w 0. В этом случае А0= .

На резонансной частоте при условии, что b << w₀ и w _рез » w₀, амплитуда колебаний равна

, поэтому отношение выбранных амплитуд 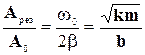= Q, т.е. амплитуда при резонансе увеличивается в Q раз (Q - добротность системы). При достаточно высокой добротности смещение отдельных частей системы может превышать пределы допустимых деформаций, что приведет к разрушению системы. Особенно опасны такие явления там, где разрушение колеблющейся системы может повлечь за собой гибель людей, - например, на механическом транспорте. Вращение винтов, валов с определенной частотой может вызвать резонансные колебания корпусов самолетов, судов и машин. Чтобы предотвратить подобные явления, конструктора вынуждены заранее тщательно рассчитывать как собственные частоты транспортных средств, так и возможные частоты, возникающие при различных режимах работы двигателей.

Важной характеристикой резонансной кривой является так называемая ширина кривой. Шириной резонансной кривой называют область частот, близких к резонансной частоте, на которых относительное уменьшение «реакции» системы на внешнее воздействие не превышает 30% (точнее в 1/ раза) относительно «реакции» на резонансной частоте (рис.5.12). Степень задаваемого ослабления носит субъективный характер и связана со слухом человека. Многочисленные измерения показали, что человек «на слух» различает громкости различных источников звука, если их амплитуды отличаются на 30%. Если громкости отличаются на меньшую величину, то человек воспринимает как одинаковые. Другими словами, все звуки при их резонансном усилении, лежащие в области ширины резонансной кривой, будут казаться человеку звуками с одинаковой громкостью. Это важно учитывать при конструировании и изготовлении музыкальных инструментов.

Дата добавления: 2014-12-10